光伏电池阵列布置模式的探讨
■ 谢丹,鞠健,于苗苗,赵楠
(1.辽宁电力勘测设计院;2.辽宁太阳能公司)
一 引言
太阳能是取之不尽,用之不竭的清洁能源,是国家大力推广的绿色清洁能源之一。太阳能的能量密度低,而且它因地而异,因时而变,对地面条件要求较高。大型地面光伏电站往往需相当大的采光面才能满足使用要求,因此导致光伏电站的发展受到制约。光伏发电系统的主要部件有太阳能电池板、控制器、逆变器等。由于光伏组件的输出电压不高,需一定数量的光伏组件经过串并联构成方阵,将其所接收到的太阳光能直接转换为电能。因此,在光伏发电系统中,光伏电池板方阵是占地面积最大的部件,对电池板方阵的布置优化成为各个工程项目重点研究内容。
二 太阳能电池板的构成
单体太阳电池的输出电压、电流和功率都很小,为了提高输出功率需将多个单体电池合理地连接起来,并封装成组件。光伏组件主要是由电池片、前罩、保护膜、透明软塑料、钢化玻璃、后面板和框架等组成。太阳能电池板是由多个光伏组件串联组成,为了便于检修和维护,地面大型光伏电站一般有横向和竖向两种组成形式,如图1所示。

通过比较这两种布置方式,其占地面积相同。但是在电线的使用量上,竖向要少于横向,因此在设计上较多采用竖向布置。以下在讨论光伏阵列布置时以竖向布置为例。
三 影响光伏发电量的因素
一般来说,决定太阳电池发电量的是太阳电池方阵面上所获得的辐射量,也就是说,太阳能电池板的发电量与电池方阵面上所获得辐射量的多少有直接关系。太阳能电池板面上的总辐射等于直接辐射与散射辐射之和[1]。直接辐射的变化与太阳高度角、大气透明系数、海拔高度和纬度有关。
一般情况下,发电量的计算是在光伏阵列表面完全没有阴影的前提下得到的。据统计,在晴天,白天散射辐射量占总辐射量的10%~20%[2]。而且太阳能电池板不能被日光直射到时,散射光也可发电[3]。
光照强度对光电压的影响很小,在温度不变的情况下,当光照强度在400~1000W/m2范围内变化时,光伏电池组件的开路电压基本保持恒定。因此,光伏电池组件的功率和光照强度基本成正比[4]。
四 最佳倾角及阵列间距选择
最佳角度就是太阳能电池板平面与水平地面的夹角,最佳倾角与当地的地理纬度有关,倾角不同,不同月份方阵面上接收到的太阳辐照差别很大。但在设计中,也要考虑到积雪滑落的倾斜角(斜率大于50%~60%)等方面的限制[5]。特别是在并网发电系统中,宜根据当地太阳辐射能量的变化,得到“最佳倾角”使太阳能电池板在一年中的发电量最大,并不一定优先考虑积雪的滑落。
太阳高度角α的计算公式为:
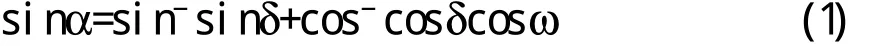
其中:¯为当地纬度(0~90¡);δ为太阳赤纬角,是阳光射线与赤道平面的夹角;ω为时角(地球自转一周360¡,24h),取15¡/h。
太阳方位角β的计算公式为:

关于上述参数的对应关系详见图2,其中Z为电池板倾角。以沈阳为例:(纬度:41.3N,经度:123E)给定建设区域,电池板性能参数参照245W产品,电池板的规格为:1.65m×0.99m。电池阵列模块安装方位角采用正南方向,安装方式按固定倾角,光伏子阵列由竖向放置2排组成,每排10个,共20个串联一组为一个阵列。通过软件计算,当太阳能电池板固定倾角为40¡时,电池板所接收到的太阳辐射量最大。
沈阳地区纬度¯为41.3¡,早上9点时角ω=-45¡,赤纬角δ=-23.45¡,阵列的斜面长度约为3.3m,阵列宽约为10m。假定在1000m2的面积上进行太阳能电池板的布置。

当纬度较高时,方阵之间的距离加大,其占地面积也会增加。对于有防积雪措施的方阵来说,其倾斜角度大,因此使方阵的高度增大,为避免阴影的影响,相应地也会使方阵之间的距离加大。通常在排布方阵阵列时,应分别选取每个阵列的构造尺寸,将其高度调整到合适值,从而利用其高度差使方阵之间的距离达到最小。
阵列的影子长度因安装场所的维度、季节、时间不同而异,如果在影子最长的冬至,从9:00~15:00,影子对阵列没有影响,说明太阳电池输出功率不受影响[6]。在地面大型光伏电站的太阳能电池板的布置上,为了有效利用电池组件,其前后排的间距是考虑在太阳高度角最低的冬至那一天,从当地时间9:00~15:00之间,其电池板组件的影子互不影响,即前排电池板的阴影不落在后排电池板上,以此保证整个电池阵列产生最大的发电量。
五 数据分析
首先,对阵列的倾角进行调整,通过计算发现,随着倾角的变化,光伏电站的装机容量随之变化,因此发电量也随之改变。为了更明确三者之间的关系,我们略去其他客观因素的影响(如道路、坡度等)。以沈阳为例,对数据进行了综合分析,辐照度与倾斜角度关系曲线如图3所示。

在辐照度与倾斜角度关系上,利用PVSYST软件计算,生成对应数据表并转换成图3。经分析,可看出当太阳能电池板的倾角发生改变,倾斜面上的每m2可接收到的辐照能量将随之变化,并且在某个角度时其辐照量最大。另外,对于一定的地域,倾斜角度的减小,太阳能电池板的布置容量将增加。反之,对于一定装机容量,倾斜角度的减小,土地的利用面积将减少。
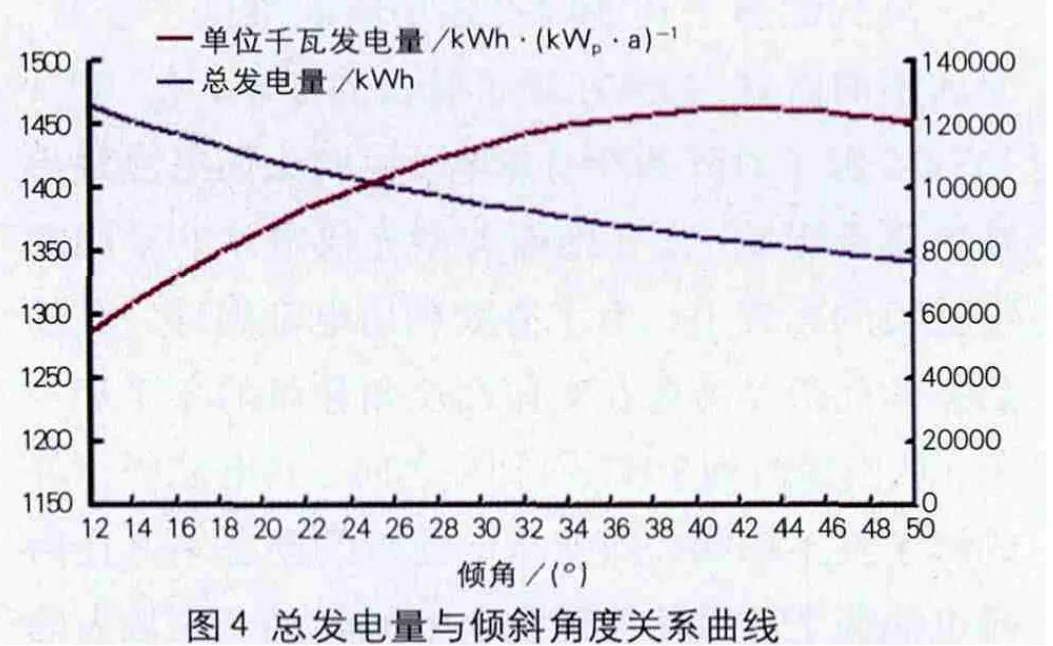
图4显示对应一定地域面积,随着倾斜角度的减小,总发电量随之增加。经过分析发现,电量增加的原因是由于太阳能电池板的布置容量增加,从而使总发电量发生显著变化。
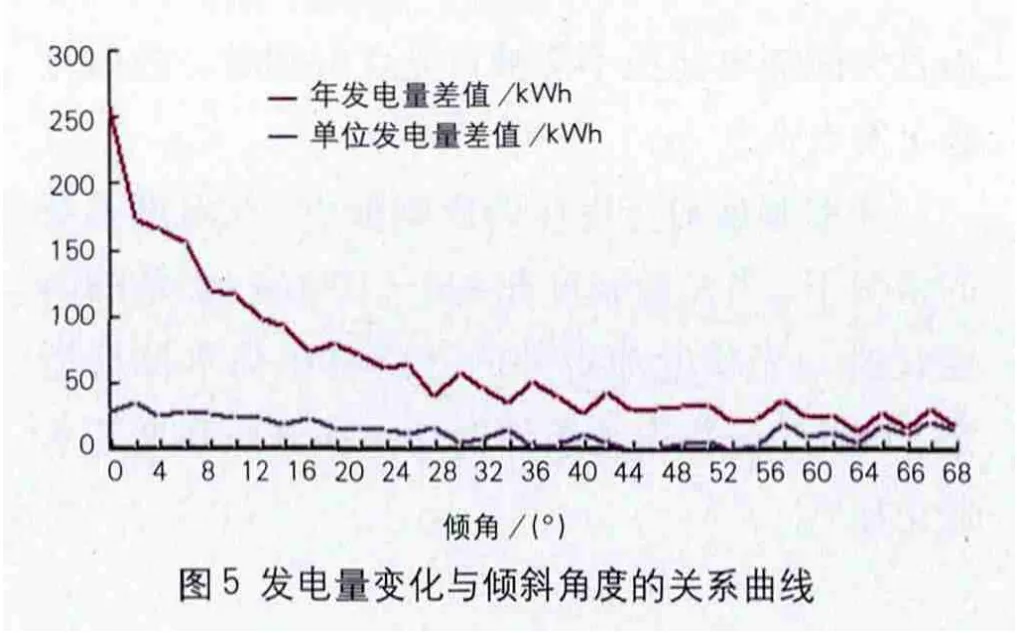
发电量与倾斜角度的关系曲线如图5所示,从图5可知,太阳能电池板的利用率随着倾斜角度的变化变化。全年最佳倾角与当地直接辐射量占总辐射量比例有很大关系,在我国绝大多数地区,全年最佳倾角要小于当地纬度[7]。得出当大型地面光伏电站采用固定最佳倾角布置模式,可提高光伏组件的利用效率,在一定条件下降低光伏电站的造价。在最佳倾角的选择上除综合考虑连续性、均匀性和极大性外,还应考虑经济性[8]。
六 建立模型及分析
根据近期做过的工程统计,作为太阳电池阵列的主要制约条件的土地资源越来越紧张,土地的价格越发不容忽视,因此引入土地价格作为参考因素。我们建立了一个工程特征数学模型:

其中,项目总投资计及各主要设备购置、土建安装、征占补偿等投入成本;可上网电量计及组件性能、系统效率、气候、污染、倾角等。
在本模型建立中,以沈阳地区为例,筛选几个主要影响因素,包括站址位置、太阳能辐射数据、太阳能电池板性能参数、电池组件的市场价格、土地价格等。通过对前面所列前提条件的测算,在最佳倾角附近出现发电成本投资最低区。发电成本与倾斜角度关系曲线如图6所示。

利用模型分析时,根据工程特性,提取出有代表性的太阳能电池板和土地的价格作为发电投资成本估算的风向标。通过参考量的双向变化,我们发现前文所说的“最佳倾角”并不是工程应用中的最佳倾角,进而在模型中从市场波动和资源利用两个角度对光伏阵列的倾角的选取形成客观依据。
通过该模型的应用分析,可得到更为实用的太阳能光伏组件的最佳倾角,进而减少土地占用面积,提高土地利用率,降低投资成本,提高了投资收益率。通过工程中对沈阳地区的综合测算,采用新的倾角选择理论,可提高发电量约10%以上。
七 结束语
随着太阳能电池板价格的降低,太阳能发电迎来了快速发展的阶段。而在光伏产业快速发展的同时,其制约因素也逐渐显露出来,土地就是首当其冲的要素。因此,优化电池板的布置模式,提高发电量和土地的利用率成了当前亟待解决的问题。
(1) 通过模型分析,可看出投入与产出的平衡点已颠覆传统布置模式中的“最佳倾角”的选择思想。从模型分析,随着组件成本与土地价格的逆向变化,其效果更加明显。因此建议在工程设计中,应根据当地条件,增加土地利用率(即土地回报率)分析。
(2) 随着土地价格的上涨,在特定工程条件下,度电投资成本会随着倾斜角度的改变而改变。因此在大型地面光伏电站的建设时,应根据工程特性合理确定方位角和倾斜角的同时,还应进行全面考虑,才能使光伏电站达到最佳运行状态。
(3) 利用该模型对“金太阳”和分布式光伏项目进行分析,也可以为项目设计提供重要的参考依据。
[1] 王长贵, 王斯成. 太阳能光伏发电实用技术(第二版)[M] . 北京: 化学工业出版社, 2009.
[2] 崔容强, 赵春江, 吴达成. 并网型太阳能光伏发电系统[M] . 北京: 化学工业出版社, 2007.
[3] 黄汉云. 太阳能光伏发电应用原理[M] . 北京: 化学工业出版社, 2009.
[4] 李瑞生, 周逢权, 李燕斌. 地面光伏发电系统及应用[M] . 北京:中国电力出版社, 2011.
[5] 黄汉云. 太阳能光伏发电应用原理[M] . 北京: 化学工业出版社, 2009.
[6] 吴永忠, 邹立裙. 光伏电站太阳能电池阵列间距的计算[J] . 能源工程, 2011, (1): 39-40.
[7] 杨金焕, 毛家俊, 陈中华. 不同方位倾斜面上太阳辐射量及最佳倾角的计算[J] . 上海交通大学学报, 2002, 35(7): 1032-1036.[8] 刘祖明, 廖华, 李耀飞, 等. 固定式光伏方阵最佳倾角[J] . 太阳能学报, 1992, 13(4): 387-388.
