轨检小车用于高速铁路轨道几何状态检测的关键问题研究

张 勇，田林亚，王 建，杨建中，产光杰

(1.河海大学地球科学与工程学院，南京 210098;2.西南交通大学地球科学与环境工程学院，成都 610031;3.沪宁城际铁路股份有限公司，南京 210042)

随着中国经济的快速发展，在中国建设了多条高速铁路，如京沪高速铁路、郑西高速铁路、武广高速铁路等。高速铁路对线路轨道的平顺性有着极高的要求，其中，轨道的几何状态检测在高速铁路建设过程中尤为重要。工程实践中，测量人员采用一种名叫“轨检小车”的设备来检测铁路轨道的安装精度，即检测2根钢轨的实际位置与设计位置的偏差。在这种设备中，高精度地计算线路的设计坐标和实测坐标成为了一个难点。

通常情况下，轨道里程的坐标是由线路设计参数和指定里程作为起算数据进行计算的，但是在高速铁路中，轨检小车架设在轨道上，直接测量的是轨检小车上棱镜点的坐标，该坐标属于非中心坐标，若想知道当前轨检小车位置的线路中线设计坐标及其两轨顶坐标，只有通过实测的轨检小车棱镜坐标采用数值迭代方法推算出轨检小车当前位置的线路中心里程，再由里程计算线路中心点的设计坐标和横断面设计方位角，最终计算左右钢轨实际状态以及与设计坐标的差值。

1 轨道几何检测计算模型

1.1 曲线要素的计算

高速铁路线型设计时，也会因各种原因或需要而改变线路的方向，在转向的地方用曲线将2条直线密切地衔接起来。曲线主要分为圆曲线和缓和曲线，在国内，缓和曲线一般采用螺旋线型，在国外，缓和曲线多采用抛物线型。

带有缓和曲线的圆曲线有5个要点，分别为直缓点(ZH)、缓圆点(HY)、交点(JD)、圆缓点(YH)、缓直点(HZ)，曲线的切线长T、曲线长L、外矢距E0和切曲差q等称为曲线要素，其计算公式为［1]

式中，R为圆曲线半径;l0为一侧缓和曲线长度;α为曲线转向角。

1.2 根据线路里程计算轨道坐标

如图1所示建立局部坐标系，其原点为ZH点，x轴由切线定义。设li为任意一点i距ZH点的曲线长，Li为i点的里程，L0为ZH点的里程，则li=Li-L0。

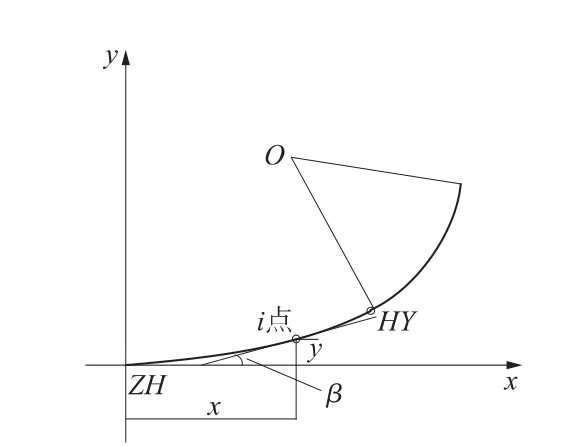
图1 切线坐标系

在第一缓和曲线段，即ZH～HY段，距ZH点曲线长为li的i点坐标(xi，yi)的计算公式为

其中，C=Rl0为常数;β为i点切线的倾角。

将坐标(xi，yi)进行旋转变换，求得i点在线路测量坐标系中的坐标(Xi，Yi)和该点切线方向的方位角Ai，其坐标旋转公式为［1]

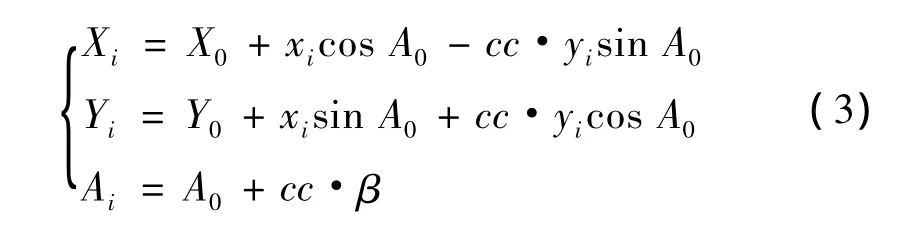
其中，A0=AZH-JD为ZH与JD连线的方位角;X0=XJD+Tcos(A0+180°);Y0=YJD+Tsin(A0+180°);线路左偏时cc=-1，线路右偏时cc=1。

在圆曲线段，即HY～YH段，距ZH点曲线长为li的i点坐标的计算公式为［1]

其中，l0为缓和曲线长。

将坐标(xi，yi)按式(3)进行旋转变换，求得i点在线路测量坐标系中的坐标(Xi，Yi)和该点切线方向的方位角Ai。

在第二缓和曲线段，即YH～HZ段，先根据式(2)计算局部坐标(xi，yi)，此时li=L-(Li-L0)其中L为式(1)中的曲线长，再根据式(3)计算i点在线路测量坐标系中的坐标(Xi，Yi)和该点切线的方位角Ai，此时，X0、Y0、A0、cc2应根据下面公式计算［1]

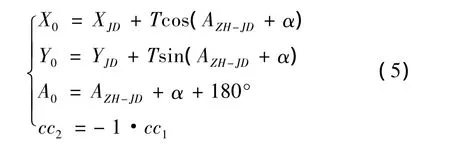
其中，α为线路的转向角。

1.3 根据非中心坐标计算线路里程

由于轨检小车的棱镜不是位于轨道的中间，要根据棱镜坐标计算轨道中线点坐标，就需要知道轨检小车的横向方位角，这个方位角通常采用轨道设计的横断面方位角。

轨检小车横向方位角，即为轨检小车棱镜点投影到线路中线上的点的设计横断面方位角，其中轨检小车上棱镜点的线路坐标(X0，Y0)，即非线路中线点FP(图2)，要投影成中线上TP点的线路坐标(X，Y)应同时满足两个重要条件，第一个条件是FP点和TP点之间的距离D是FP点到线路距离最短的，第二个条件是TP点在线路中线上。

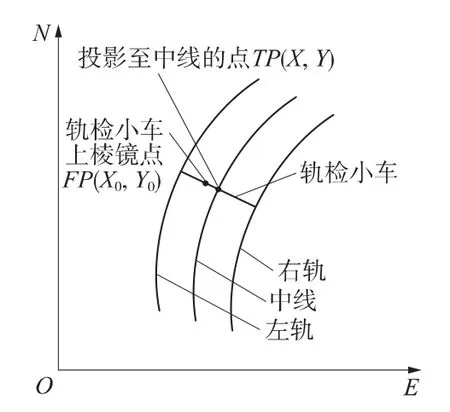
图2 棱镜点投影

由非线路中心点计算里程分3种情况，即直线段、圆曲线段、缓和曲线段，其中直线段和圆曲线段计算方法相对容易，在缓和曲线段比较复杂，本文采用牛顿迭代法计算。

1.3.1 点与线路的位置关系

在计算模型中使用了缓直点、直缓点等点的坐标，在实际情况中，存在多个拐弯时也就存在多个曲线段，因此先要确定轨检小车在哪个曲线段。

首先，计算线路上所有直缓点(ZH)、缓圆点(HY)、曲中点(QZ)、圆缓点(YH)、缓直点(HZ)处的横断面方位角和坐标。把这一系列的点按照顺序排列组成链表 Li(i=1，2，3，…，n)，每次取 i、i+1(i=0，1，…，n)点，并与 FP 点计算方位角得 Ai，FP、Ai+1，FP，当满足 Ai，FP＞ Ai且 Ai+1，FP＜ Ai+1时，FP 点位于由 Li和 Li+1构成的区间内，如果不满足条件，则取i=i+1，直到满足条件。

1.3.2 直线段计算模型

由前一个曲线段HZ点的线路坐标(X1，Y1)和后面曲线段ZH的线路坐标(X2，Y2)，构造HZ点与ZH点之间直线段的直线方程

其中，A=(Y2-Y1);B=-(X2-X1);C=-［(Y2-Y1)X1-(X2-X1)Y1]。

如图3所示，FP点到直线的距离为 D1=，FP点到前一个HZ点的距离为D2=FP点、TP点和前一个HZ点构成了直角三角形，所以投影点距HZ点的距离为，则有

其中，LHZ为前一个HZ点的里程;LTP为投影点的里程;LFP为非线路中心点的里程，即轨检小车处的里程。

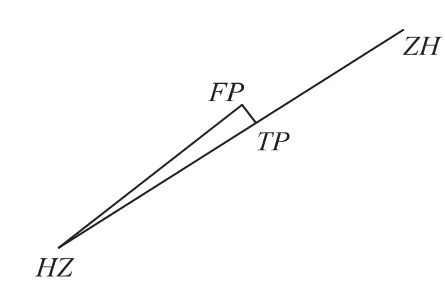
图3 直线段投影

1.3.3 曲线段计算模型

在曲线段由里程计算坐标的时候，都是先采用一个局部坐标系进行计算，再将其转换到线路坐标系中，本文的后续推导都是基于局部坐标系进行的，而由全站仪测得的轨检小车棱镜点FP的坐标(X0，Y0)是线路坐标系下的坐标，所以要先将FP点的坐标通过平面坐标转换为局部坐标系下的坐标(x0，y0)。

在圆曲线段时，首先根据式(8)由HY点线路坐标(XHY，YYH)、HY点切线方位角 AHY和圆弧半径 R，计算出圆心坐标(XC，YC)，其几何关系见图4。

图4 圆心坐标的计算

然后，根据式(9)计算HY点与FP点的圆心角θ，求到圆心角θ后，根据l=θR，计算TP点到HY点的距离LD，则LTP=LYH+LD，也就是轨检小车处的里程。

在缓和曲线段时，FP点和线路上任意一点的距离公式为D=(xi-x0)2+(yi-y0)2，将式(2)代入并求导得

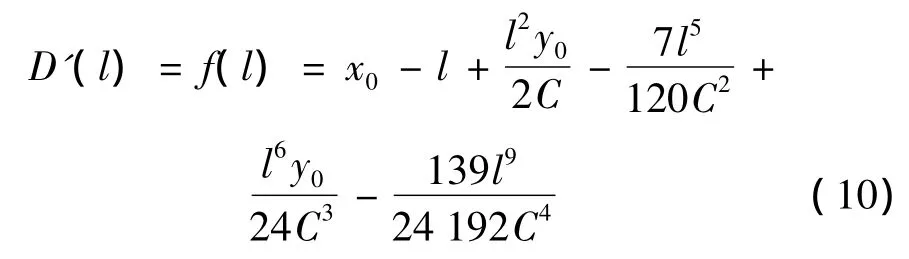
因为FP点至线路投影点TP的距离是最短的，D'(l)=f(l)=0，则按照牛顿迭代法公式(11)进行反复计算，l的初值可以直接取该曲线段的ZH点或者HZ点的里程。

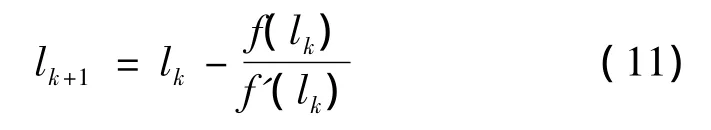
求得精确曲线长lk+1后，在第一缓和曲线段时，TP点的里程LTP=LZH+lk+1，在第二缓和曲线段时TP点的里程为LTP=LHZ-lk+1，TP点的里程也就是轨检小车处的里程。

2 实例计算

根据上述计算模型，笔者研制了基于轨检小车的轨道几何状态检测计算软件，现利用某铁路线路的部分设计参数和测量数据，对上述计算模型的正确性和有效性进行验证。线路部分设计参数见表1，采用自动全站仪测量轨检小车上的棱镜在线路坐标系中的坐标见表2，根据表1中的线路设计参数，依据本文研究的模型进行仿真计算，计算结果一并列于表2。

表1 某线路部分设计参数

表2 轨检小车棱镜中心坐标

为验证轨道几何检测计算软件的内符合精度，现采用以下方案:已知轨检小车棱镜点的里程，那么该点的设计方位角可用得到的里程求得，该里程的轨道设计坐标数据也同时可以求得。根据轨检小车的设计结构(轨检小车的棱镜与小车中心的设计偏差为30 cm)，分别采用表2中的里程和设计方位角、设计偏差计算线路的中心坐标并进行比较，结果列于表3。

由表3中的数据看出，2种方式求得的坐标偏差均不大于±0.2 mm，说明本文研究的计算模型是严密的，编写的程序是正确的，满足高速铁路轨道几何状态检测的计算要求。

表3 线路中心坐标比较

3 结语

(1)在高速铁路建设中，自动全站仪结合轨检小车检测铁路轨道几何状态的方法已得到采用，研究基于轨检小车的轨道几何状态检测计算模型，开发高精度的配套测量软件，有助于发挥其检测性能，提高作业效率。

(2)计算轨检小车所在位置的线路中心里程，对计算轨道坐标相对于设计坐标的偏差非常重要，直接关系到轨道的不平顺性调整。本文分直线段、缓和曲线段及圆曲线段分别研究严密的计算模型，计算结果可靠，精度较高，算法虽然采用了数值迭代计算，但由于高速铁路具有较好的线性以及牛顿迭代法具有良好的收敛性，计算效率也较高。

(3)本文是针对缓和曲线为螺旋线的情况进行研究的，笔者研制的轨道检测计算软件中还包括三次抛物线等其他线型，可以用于高速铁路平顺性等检测。

［1]张正禄，等.工程测量学［M].武汉:武汉大学出版社，2005:163-169.

［2]张忠良，杨友涛，刘成龙.轨道精调中后方交会点三维严密平差方法研究［J].铁道工程学报，2008(5):33-36.

［3]任晓春.客运专线无砟轨道精密工程测量平面坐标系的探讨［J].铁道勘察，2008(2):1-4.

［4]朱超，许昌，王超.测量机器人GeoCOM接口技术的应用与开发［J].北京测绘，2007(5):35-38.

［5]张冠军.铁路工程测量中几种平面坐标系的建立［J].测绘工程，2010，19(2):75-77.

［6]Fu Wenjuan，Chen Chunjun.Robust Spectral Estimation of Track Irregularity［J].Journal of Southwest Jiaotong University，2005(1):44-48.

［7]杨成宽.GEDO CE轨道检测系统在无砟轨道施工测量中的应用［J].铁道工程学报，2009(3):57-61.

［8]胡庆丰.安博格GRP1000轨检小车进行无砟轨道检测的作业方法［J].铁道勘察，2008(3):17-19.

［9]谯生有，周建军，周建东.客运专线无砟轨道CPⅢ精密控制网测量探讨［J].铁道标准设计，2009(S1):36-39.

［10]彭学理.宜万铁路双块式无砟轨道的测量控制与精度效果分析［J].铁道标准设计，2010(8):46-48.