蛋形断面隧洞正常水深的简易算法
滕 凯
(齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)
蛋形断面隧洞正常水深的简易算法
滕 凯
(齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)
由于蛋形断面隧洞形式相对比较复杂,正常水深计算需完成较复杂的超越方程求解,通过解析法无法直接获解。常规的图表法,实际应用中不仅依赖图表且存在查图(表)取值的人为误差;试算法由于公式分段且表达形式为非常复杂的超越方程,重复计算工作量大、效率低。依据优化拟合理论,以标准剩余差最小为目标函数,在工程适用参数范围内,经拟合计算获得了由一个通用算式表达、形式简单直观、便于实际应用、计算精度满足设计要求(最大误差为0.729%)的近似公式,具有一定的实用推广意义。
蛋形过水断面;正常水深;优化拟合;近似计算
蛋形断面具有受力条件好、过流能力强、适应地质环境突出、节省空间及材料的显著特点,但由于该种断面形式复杂,施工难度相对较大,在一定程度上影响了实际工程推广。机械化施工技术及工艺的不断提高,为该种断面在工程上的应用创造了有利条件,并已在近几年的水利水电供排水工程中得到应用[1-2]。有理由相信,该种断面必将在未来的输配水工程中显现越来越广阔的应用前景。
由于该种断面由4个圆心、3个不同半径的4条圆弧曲线构成,几何图形复杂。正常水深计算不但涉及3个分段公式,而且需完成超越方程求解,无法直接获得。常规解法[3-5](图表法、试算法)过程繁、精度低,利用微机编程求解又不便实际工作[6],而将该种形式蛋形断面正常水深计算的分段函数统一由一个近似计算公式表示及解算,到目前为止尚未见到。为了解决常规算法所存在的问题,本文依据优化拟合原理,以标准剩余差最小为目标函数,经逐次逼近拟合计算,获得了在工程实用范围内用一个计算通式直接完成求解计算的解析式,使求解计算过程更加简捷、直观,便于实际应用。
1 正常水深的基本计算公式
根据水力学原理[7],正常水深的基本计算方程为

式中:Q为隧洞设计过流量(m3/s);A为过水断面面积(m2);X为湿周(m);i为隧洞底坡降;n为隧洞内壁糙率系数。
1.1 蛋形断面水力要素
蛋形过水断面(见图1所示),断面结构是由半径分别为0.5r,r及3r(r为顶弧半径,m)的4段圆弧曲线构成的封闭式复合断面,断面计算图见图1(b)。

图1 蛋形过水断面示意图Fig.1 Egg shaped flow section


式中:θi(i=1,2,3)分别为蛋形断面在3个不同区段水深所对应的圆心角(见图1(b)所示)。
1.2 蛋形断面正常水深基本计算公式

式中:k为已知综合参数;h0为蛋形断面的正常水深。
经整理即可获得求解蛋形过水断面正常水深的基本公式为:
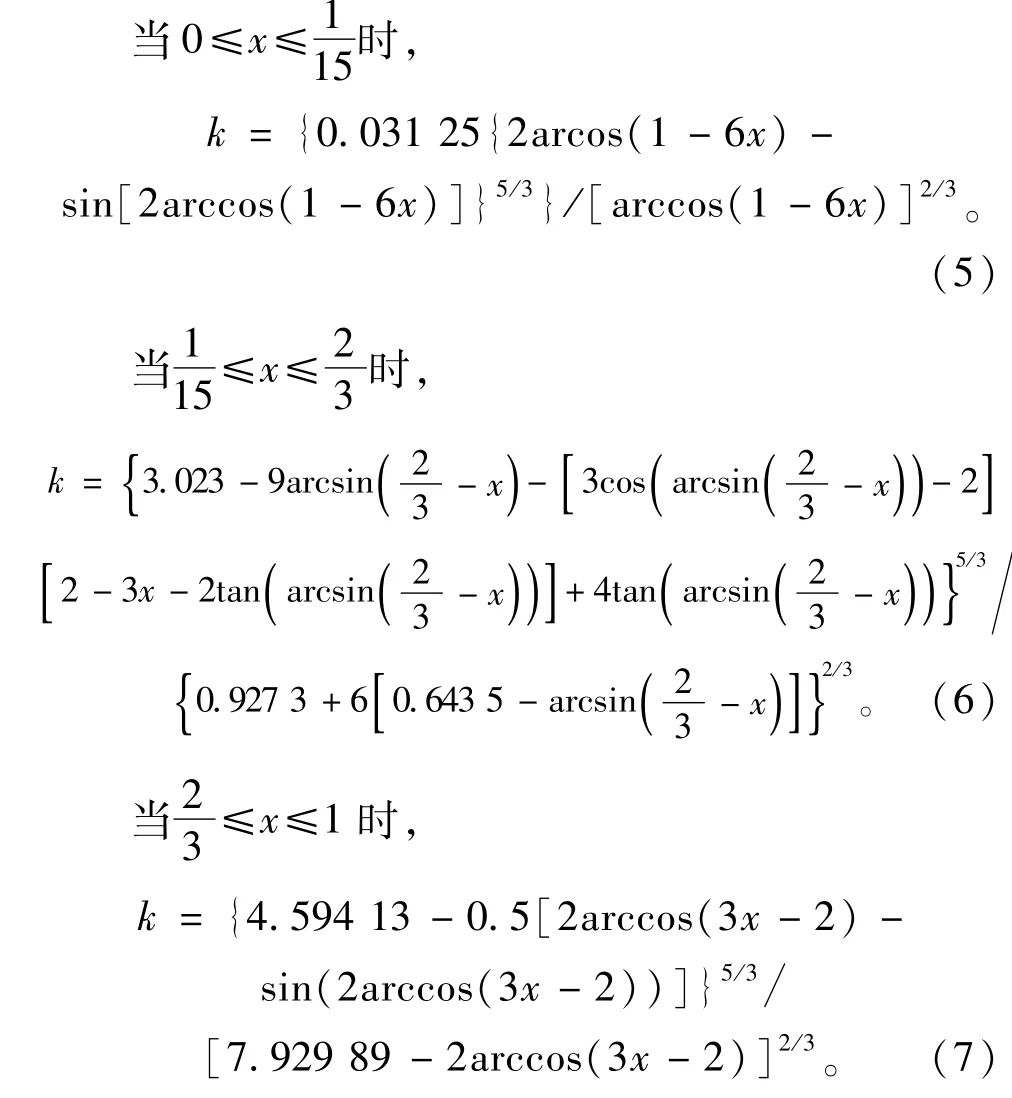
利用式(5)至式(7),即可根据已知的k值采用相应区间的计算公式通过非解析法(图解法或试算法)完成无量纲水深x的求解,进而由下式求得正常水深,即

由式(5)至式(7)可见,在理论上,x的取值范围为[0,1],而在实际工程中,x<0.04的情况极为少见;同时,考虑为避免洞内产生明满流交替现象,《水工隧洞设计规范》[8]规定,在低流速恒定流情况下,洞内水面线以上的富余空间面积不宜小于隧洞断面积的15%,且净空高度不应小于0.4 m,由此可以求得x<0.83,因此本文将x的取值范围确定为[0.04,0.83],相应参数k的取值范围为[0.009 5,3.069 4]。
2 蛋形断面正常水深的近似公式及精度分析
2.1 拟合公式的建立
由式(5)至式(7)可见,利用已知的参数k值求解x涉及非常繁复的超越方程,无法直接获解。为解决超越方程求解问题,在工程实用参数范围内(即0.04≤x≤0.83,0.009 5≤k≤3.069 4),假定函数xi=f(k)(i=1,2,3)可以分别替代式(5)至式(7),并依据式(5)至式(7)展绘x-k关系曲线(如图2所示)。

图2 x-k关系曲线Fig.2 Curves of x versus k
由图2可见,x与k具有较好的指数关系,在兼顾拟合精度高、表达形式简单2个必备条件下,初选拟合函数为

式中A,B及α分别为待定系数及指数。
采用数值拟合分析的方法,以标准剩余差最小为目标函数[9-16],即

式中n为拟合计算的数组数。
经逐次逼近拟合[17-18]即可获得A=0.419 95,B=0.011 2,α=0.563 2,进而完成式(9)的拟合相对误差计算,并绘制其x-k关系曲线,如图2所示。由图2及计算比较可见,式(9)的最大正、负拟合相对误差分别为3.90%和-3.52%,且拟合曲线的曲率半径随k值的增大由大于理论曲线曲率半径到小于理论曲线曲率半径,考虑在0<β<0.5π范围内,始终有tanβ/β>1,且随着β值的增大,tanβ/β的比值呈非线性逐渐增大,所以可将拟合式(9)进一步优化为
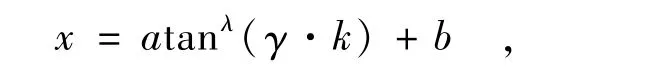
式中a,b,γ及λ分别为待定系数及指数。
采用与式(9)相同的逐次逼近拟合计算过程,即可获得式(5)至式(7)的最优拟合替代函数为
x=0.922tan0.52(0.22k)+0.002 5 。(10)
利用式(10)即可根据已知的k值直接求解无量纲水深(充满度)x,进而完成正常水深h0计算。
由式(10)也可推求出在已知蛋形断面充满度x值情况下的过水流量Q,即为

2.2 拟合公式的精度分析
为比较式(10)与3个分段公式(5)至式(7)的拟合精度,在工程实用参数范围内,选取不同的xi,并根据xi所在区间代入与其相对应式(5)(或式(6)、或式(7))即可分别计算出与之相对应的ki,再将ki代入式(10)求得与之相对应的x′i(x′i为近似计算值),并将x′i-ki关系曲线展绘于图2,同时由下式完成拟合相对误差计算。

式中:zi为拟合相对误差(%);i为拟合计算的第i个数据比较(i=1,2,3,…,n),计算结果见表1所示。
由图2及精度比较表1可见,在工程实用参数范围内,本文式(10)的拟合曲线几乎与3个区段公式(5)至(7)的理论曲线完全重合,其最大拟合替代相对误差仅为0.729%,且位于工程实用参数的端点,拟合相对误差小于0.5%和0.1%的点分别占总计算点数的94%和61%,可见,本文式(10)具有较高的拟合替代精度,完全可以满足实际工程的设计精度要求。
3 应用举例
例1:已知某水库引水隧洞的设计流量为Q=38 m3/s,设计横断面形式为蛋形,顶拱半径r=2.5 m,洞底设计坡降i=1/2 500,洞内壁糙率系数n=0.014。试计算隧道内的正常水深h0值。
根据已知参数即可求得k=2.310 51,将k=2.310 51代入式(10)即可求得无量纲水深x为
x=0.922tan0.52(0.22k)+0.02 5=0.682 69。
则可求得正常水深h0=3rx=5.120 m,通过微机编程可求得该断面正常水深的精确解为h0=5.116 m,本文简化公式计算成果的相对误差为0.078%。

表1 式(10)拟合精度比较Table 1 The fitting accuracy of equation(10)
例2:例1中其它参数不变,试计算当隧洞的正常水深h0=3.5 m时洞内的通过流量Q。

利用式(6)可求得k=1.188 32,进而可求出洞内通过流量的精确解本文公式计算成果的相对误差为0.05%。
4 结 语
由于蛋形过水横断面的几何图形比较复杂,目前延用的常规计算方法不便实际工作。本文依据优化拟合理论,经逐次逼近计算,获得了可直接完成蛋形过水断面正常水深求解的近似计算通式,与其它公式比较具有以下特点:
(1)所建立的简化公式在工程实用参数范围内不分段,可使正常水深计算由一个表达通式完成,避免了分段公式在求解计算中所带来的诸多不便。
(2)公式的表达形式更加简捷、直观,更便于记忆,实际工作仅借助计算器即可实现快速完成解算,有利于广大工程技术人员实际应用。
(3)精度分析及算例计算结果比较表明,在实用参数范围内,本文公式具有较高的计算精度,最大计算相对误差仅为0.729%,完全可以满足实际工程的设计精度要求。
[1] 傅功年,唐耿红.冉铺湾隧洞衬砌断面型式选择[J].人民长江,2002,33(5):14-16.(FU Gong nian,TANG Geng hong.Selection of the Cross section Type of the Lin ing of Ranpu Bay Tunnel[J].Yangtze River,2002,33(5):14-16.(in Chinese))
[2] 王子宜.蛋形衬砌在白莲灌区武家坳隧洞中的应用[J].湖南水利水电,2006,(6):70-71.(WANG Zi yi.Application of Egg shaped Tunnel Lining toWujia’ao Tun nel in Bailian Irrigation Area[J].Hunan Hydro and Pow er,2006,(6):70-71.(in Chinese))
[3] 华东水利学院.水工设计手册[M].北京:水利水电出版社,1986.(Hohai University.Hydraulic Design Manual[M].Beijing:China Water Power Press,1986.(in Chi nese))
[4] 宁希南.蛋形断面管道简明水力计算及其诺谟图[J].林业建设,2007,(5):22-25.(NINGXi nan.Simple Hy draulic Calculation for Pipes in Egg shaped Cross section and Its Nomogram[J].Forestry Construction,2007,(5):22-25.(in Chinese))
[5] 陶 冶,贾 悦.蛋形断面排水无压管道水力计算及其水力要素分析[J].给水排水,2009,35(增1):428-430.(TAO Ye,JIA Yue.Hydraulic Calculation and Hydraulic Element Analysis for the Non pressure Pipeline in Egg shaped Cross section[J].Water and Wastewater Engi neering,2009,35(Sup.1):428-430.(in Chinese))
[6] 吴军君,许小健,倪宝艳.城门洞形断面输水隧洞临界水深度的计算方法[J].城市道路与防洪,2007,(9):160-162.(WU Jun jun,XU Xiao jian,NI Bao yan.Calcula tion Method for the Critical Depth of Water Conveyance Tunnelwith Horseshoe Shaped Section[J].Urban Roads and Flood Control,2007,(9):160-162.(in Chi nese))
[7] 张志昌.水力学[M].北京:中国水利水电出版社,2011.(ZHANG Zhi chang.Hydraulics[M].Beijing:China Water Power Press,2011.(in Chinese))
[8] DL/T5195—2004,水工隧洞设计规范[S].北京:水利水电出版社,2003.(DL/T5195—2004,Specification of Hy draulic Tunnel Design[S].Beijing:China Water Power Press,2003.(in Chinese))
[9] 刘 刚,滕 凯.梯形断面均匀流水深的近似计算公式[J].水利与建筑工程学报,2012,10(1):41-44.(LIU Gang,TENG Kai.Approximate Calculation Formula for U niform Flow Depth of Trapezoidal Cross section[J].Journal ofWater Resources and Architectural Engineering,2012,10(1):41-44.(in Chinese))
[10]谢成玉,滕 凯.三次抛物线形渠道断面收缩水深的简化计算[J].南水北调与水利科技,2012,10(2):148-150.(XIE Cheng yu,TENG Kai.Simplified Equation of Contracted Water Depth in a Channelwith Cubical Parzbo la Section[J].South to North Water Transfers and Water Science&Technology,2012,10(2):148-150.(in Chi nese))
[11]谢成玉,滕 凯.抛物线形断面渠道均匀流水深的近似计算公式[J].水电能源科学,2012,30(7):94-95,172.(XIECheng yu,TENG Kai.Approximate Formula of Uni form Flow Depth for Parabolic Cross section Channel[J].Water Resources and Power,2012,30(7):94-95,172.(in Chinese))
[12]郑 博,滕 凯.马蹄形隧洞过水断面临界水深的简化计算法[J].中国水能及电气化,2012,(8):13-17.(ZHENG Bo,TENG Kai.Simple Calculation Method for the Critical Depth ofWater Conveyance Tunnelwith Horse shoe Shaped Section[J].China Water Power&Electrifi cation,2012,(8):13-17.(in Chinese))
[13]滕 凯.标准门洞形隧洞正常水深的简易算法[J].中国水能及电气化,2012,(9):30-33.(TENG Kai.Simple Algorithm of Normal Depth in Standard Opening Shaped Tunnel[J].China Water Power&Electrification,2012,(9):30-33.(in Chinese))
[14]滕 凯.消力池深的简化计算法[J].人民长江,2012,43(15):77-79,91.(TENG KAI.Simplified Calculation Method of Depth of Stilling Basin[J].Yangtze River,2012,43(15):77-79,91.(in Chinese))
[15]滕 凯,周 辉.弧底梯形明渠正常水深的简化计算法[J].黑龙江八一农垦大学学报,2012,24(5):85-88.(TENG Kai,ZHOU Hui.A Method of Simplified Calcula tions for the Normal Water Depth of Open Trapezoidal Channel With Arc Bottom[J].Journal of Heilongjiang Bayi Agricultural University,2012,24(5):85-88.(in Chinese))
[16]滕 凯.标准门洞形过水断面临界水深的简化算法[J].华北水利水电学院学报,2012,33(5):1-3.(TENG Kai.Simple Computation of CriticalWater Depth of Stand ard Door shaped Waterway Tunnel[J].Journal of North China Institute ofWater Resources and Hydropower,2012,33(5):1-3.(in Chinese))
[17]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.(WANG Hui wen.Partial Least Squares Regression Method and Its Application[M].Beijing:Na tional Defense Industry Press,1999.(in Chinese))
[18]阎凤文.测量数据处理方法[M].北京:原子能出版社,1988.(YAN Feng wen.Methods of Processing Measured Data[M].Beijing:Atomic Energy Press,1988.(in Chi nese) )
(编辑:刘运飞)
A Simple Calculation M ethod for the NormalW ater Depth of Tunnel w ith Egg shaped Section
TENG Kai(Qiqihar MunicipalWater Affairs Bureau,Qiqihar 161006,China)
The normalwater depth of tunnelwith egg shaped cross section involves the solution of complex transcen dental equations,and it cannotbe calculated directly by analyticalmethod.It’s redundantand inaccurate to calcu late by conventionalmethod of looking up tables and diagramswhich would causeman made errors.Meanwhile by trialmethod,the formulas are partitioned and the equations are complicated with heavy work load and low efficien cy.In this research,an approximate formulawas obtained by optimal fitting in the range of parameters applicable to practical engineering with theminimum standard residual difference as the objective function.The formula is con venient,practical,and simple in expression.Its precision also meets design requirements(maximum error 0.729%).It is of practical promotion significance.
egg shaped flow section;normalwater depth;optimal fitting;approximate calculation
TV131
A
1001-5485(2013)12-0039-04
10.3969/j.issn.1001-5485.2013.12.007
2012-11-14;
2012-12-22
滕 凯(1957-),男,黑龙江齐齐哈尔人,高级工程师,主要从事水利防灾减灾及工程优化设计研究,(电话)13704618836(电子信箱)tengkai007@163.com。

