多阶段带时间约束的变尺寸装箱问题优化研究

朱 向,雷定猷,游 伟

(中南大学交通运输工程学院,长沙410075)

多阶段带时间约束的变尺寸装箱问题优化研究

朱 向*,雷定猷,游 伟

(中南大学交通运输工程学院,长沙410075)

多阶段带时间约束的变尺寸装箱问题,是将一般的变尺寸装箱问题(VS-BPP)置于动态环境下并加入时间约束而形成的.通过合理的计划对多阶段、有交付时间要求的物品选择箱子进行装入,达到包括箱子使用成本及与物品相关时间成本在内的总成本最小化的目的.问题具有复杂、动态的特点,其在现实中的应用很多.本文将一般的带时间约束的VS-BPP置于多阶段研究框架内,建立了基于确定信息的静态模型和基于滚动更新信息的动态模型,根据问题的特点设计了基于最佳适应规则与迭代松弛定界法相结合的启发式构造算法进行求解.经过实例的运算和分析,证明了方法在求解该问题时具有有效性.

物流工程;动态优化;构造算法;变尺寸装箱;带时间约束

1 引 言

变尺寸装箱(VariableSizeBinPacking Problem,VS-BPP)问题是在经典的装箱问题基础上,将箱子扩展为多种规格而提出来的,即指将不同大小的物品分配到不同大小有容量限制的一系列箱子里,要求所使用箱子的总成本(或总数)最小,它属于典型的NP难题.目前关于VS-BPP的研究比较多,集中于如何提高算法求解的质量和速度方面[1,2],对带时间约束变尺寸装箱问题(T-VSBPP)涉及不多.文献[3]基于物品到达时间的不确定,提出了随机带时间约束的变尺寸装箱问题(ST-VS-BPP)并进行了研究,该装箱问题具有动态性特点,但主要属于单阶段问题;文献[4]针对制造商托盘装载问题建立了整数规划模型,可适应下游顾客多品种及实时性装盘要求;文献[5]针对及时生产制下实时二维切断下料问题,建立了基于滚动时域和Multi-agent方法的求解框架.基于已有研究,本文结合装箱问题在实际操作中具有的条件不确定及连续运行的特点,提出多阶段带时间约束变尺寸装箱的概念,并尝试对这一具有复杂动态特点的问题进行研究.

2 问题的描述及数学模型

2.1 问题的描述

设场地内有一系列需要装载的物品及不同规格可供装载使用的箱子,物品具有不同体积及交付时间等属性,不同类型的箱子对应不同的使用成本,且随着时间的推移,后续需要装载的物品才能陆续到达,要求基于已掌握的信息进行合理的计划安排,在完成相关物品装载任务的前提下实现包括使用成本和时间成本在内的总成本最小化.现实中与之相类似的问题很多:如在货物运输中,运量大的铁路、船舶等方式单位货运成本比较低,可实现规模经济效益,但货物集结与装运的时间较长,运量小的公路运输单位成本高,但发运时间短,可满足适时性要求较高的运输任务;同种方式不同规格的装运工具也存在成本和时间上的差异;工业生产中产品以不同单元组合进行加工成本不一样,但同时需要满足订单在时间规定方面的要求.上述问题都存在装载规格、处理成本及作业时间上的计划与协调问题,且具有实时动态的特点.

2.2 数学模型

为了使装箱计划既能满足各方面要求,又反映随时间推移动态变化的情况,可确定多阶段基于时间约束的变尺寸装箱框架来处理.首先,需要界定问题跨越的时区(如24小时),并按批量的累积规律将时区划分为若干计划阶段;再针对每个阶段累积的装载物品,按其总体积与处理的时间要求,结合期间可用箱子的装载能力,确定合理的装载单元组合,以实现各阶段总成本最小化的目的.由于多阶段带时间约束VS-BPP是在一般的VS-BPP的基础上,基于动态作业条件并考虑相关时间约束而形成的,对于动态特性问题可采取基于确定信息的静态方法和基于实时信息的动态方法[5],据此建立该问题的模型.

2.2.1 静态装箱模型

设i为物品集N={1,…,n}中的第i个需要装载的物品,物品的体积为vi,到达时间为Ai;设R={1,…,r}为可用箱子集合,其中的箱子j的装载容积为Vj,其使用成本为Cj.关于时间方面属性,设物品i到达时间为Ai,箱子j可用时刻为Aj,j在k阶段装载过程中耗费时间为Lj(考虑由固定准备时间α和与装载数量有关的可变时间两部分组成),设j装载完毕进入后续处理的时刻为tkj.根据上述设定,物品在系统中滞留的时间应为tkj-Ai,令单位时间滞留成本(如暂存成本)为W;箱子j装载完即进入后续处理阶段,设处理耗费时间为Pkj,进而可确定物品实际交付时间.设规定交付时间为Di,若存在延时设对应延迟时间为di,单位延迟成本为pi.最后关于0-1决策变量ukj和Xikj,当第k阶段箱子j被使用及物品i装入箱子j时它们取值都为1,否则为0.

首先,按照各阶段掌握的信息制定装箱计划,对应各阶段的目标函数式为

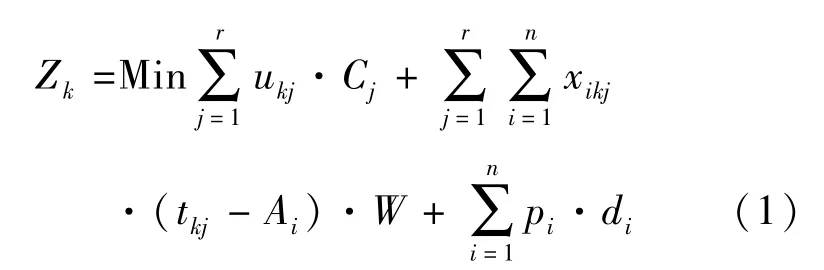
式(1)表示第k阶段装箱对应的箱子使用成本、物品停留成本,以及物品延迟交付成本之和最小化.

目标函数(2)最小化m阶段包括箱子使用成本、物品停留成本以及物品延迟交付成本在内的总成本.约束条件(3)、(4)为一般的VS-BPP问题的约束条件:式(3)对装入箱子中的物品的重量进行约束,式(4)表示一件物品只装入一个箱子.式(5)至式(7)为第k阶段箱子j装载及加工对应的时间约束:式(5)表示第k阶段箱子j开始处理时间与其到达时间及装载所耗费时间之间的关系,式(6)表示第k阶段箱子j开始处理时间与箱内各物品的到达时间及装载时间之间的关系,式(7)表示第k阶段箱子j开始处理时间与箱内各物品交付时间之间的关系.M为充分大的正数,以保证相关约束条件在物品i装入箱子j时才起作用.

2.2.2 动态装箱模型

动态装箱是基于实时更新的信息不断对计划进行修改,以反映实际变化了的情况,与实际操作中的环境相符.沿用静态装箱中确定时区的方法将整个时段按物品数量累积情况分为m阶段,当前阶段装箱计划可结合未来若干阶段进行考虑:若当前阶段为s,设每次计划所跨越的阶段数为K+1,则需对第s,s+1,…,s+K阶段一起计划.此外,由于随着时间推移后续新的需装载的物品和箱子将进一步到达,则基于当前条件形成的多阶段计划应体现不同阶段产生的作用不同,可通过引入权重加以反映.由此,得到问题在当前阶段的装箱模型为

式(9)中αs,k表示第k阶段装箱在当前(第s阶段)计划中所占的比重,考虑采用降序形式权重,可令αs,k为等,其中0≤αs≤1,具体数值可根据系统的历史运行,通过统计的方法来确定,即α=1-物品数波动率=1-新到达物品数/(已确定物品数+新到达物品数).

3 算法设计

3.1 初始解生成

由于涉及多方面因素,问题具有规模大、动态复杂的特点,为了降低难度实现问题快速求解,本文设计了启发式构造算法(Heuristics Constructive Algorithm,HCA)进行求解.它是在启发式规则的引导下逐个将物品装入箱子,这一过程需要将选择装载对象与选择空间相结合.根据问题的特点,先确定各阶段需要装载的物品,并对物品进行排序以便于后续装箱;再运用松弛定界法计算出使用箱子数量的下界,达到控制箱子总数及降低使用成本的目的;然后在此基础上采用最佳适应规则(BFD),以迭代的方式增加箱子来完成物品装箱.

3.1.1 物品排序

由于多阶段装箱的物品是随时间的推移以动态形式到达,可先根据物品到达的批次及其时间关系进行装箱阶段的划分,进而确定各阶段装载的对象,并按一定的规则对其进行排序以便于后续装载.

对物品排序时结合考虑装箱成本与时间成本两方面因素,采取聚类排序的方法来实现:设Dmin与Dmax对应为各阶段物品交付时间的上下限,将整个聚类区间分为若干簇,每簇区间的长度相等,为上下极值之差乘以某一百分比系数[1,100],第i簇对应的时段Di(θ)为

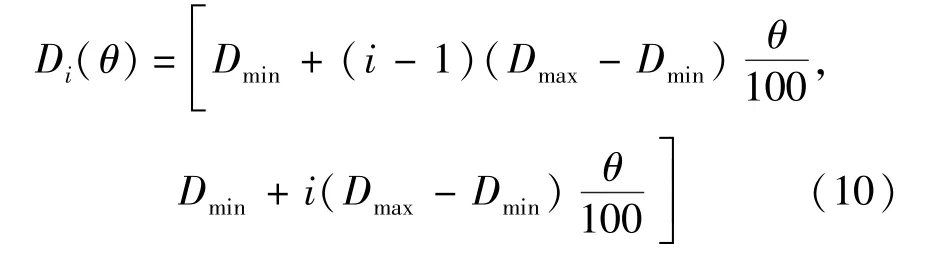
将所有物品按交付时间划分为若干簇后,按簇的标号进行升序排列,对每簇内的物品按对应的单位延迟成本pi作降序排列,单位延迟成本相同的按物品体积作降序排列.综上可得到阶段内物品的装载序列,对其中物品赋予相应的分值,给予第一个装入对象分值为n,其次为n-1,…,最后一个为1.

3.1.2 箱子定界

装箱问题基于放松约束条件的下界求解方法,可确保最终使用箱子的数量较少,借鉴文献[6]提出的松弛定界方法确定各阶段使用箱子的下界.不考虑时间约束,利用松弛方法对2.2.1中的模型实施改造,得到松弛问题模型:

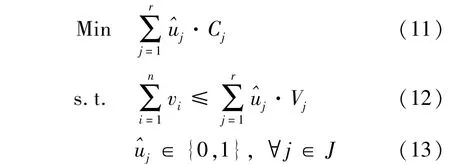
而式(14)-式(16)组成的模型为0-1背包问题模型,利用确定性方法求得下界LB(Z(y)),由此计算松弛问题的下界:LB(Z(y)),以此作为某阶段VS-BPP的箱子被选集.

3.1.3 装箱处理

物品及箱子排序后,按照序列可依次将物品装入对应的箱子.装载时优先选择已使用的箱子,当已使用箱子装不下时再打开序列中下一个新的箱子进行装载;对能装进物品且已装入物品的多个箱子,按照BFD规则选择箱子装载,即选择具有最大剩余空间(箱子的容积减去已装载物品体积和)的箱子装入当前物品.

由下界方法确定的箱子序列难以将物品全部装完,当剩余物品较多时,可对剩余物品重新计算下界,并以迭代的方式增加箱子进行装载;当经装载后剩余物品数量较少时,通过成本估算与比较来确定在本阶段增加箱子完成装载,还是将物品转移至下一阶段与后续物品合并装载.

算法1 初始解生成过程

Step 1确定多阶段VS-BPP跨越的时区T,根据已掌握的物品批次到达及交付时间信息将T分为Nj阶段,确定各阶段对应的时间范围.

Step 2对第k阶段中对应的物品,确定各物品i的交付时间di;根据di将第k阶段内物品按交付时间先后顺序分为m簇,再将每簇中物品按体积作降序排列,将各簇物品序列相连得到第k阶段的物品序列.

Step 3确定第k阶段到达的可用箱子,运用松弛定界法计算该阶段使用箱子的下界,对其按体积以降序排列得到第k阶段的箱子序列.

Step 4按物品序列选择物品、按箱子序列确定箱子,并结合BFD规则选择箱子实施第k阶段装箱,优先装入已使用的箱子,直至物品不能装入为止.

Step 5设最大箱子的体积为Vmax,若阶段k的剩余物品的总体积Vk＞Vmax,按Step 2至Step 4以迭代的方式进行装载,同时更新Vk,直至Vk≤Vmax转Step 6.

Step 6确定能装入第k阶段最后剩余物品成本最小的箱子组合,设其对应成本为Ck1;若将其转入第k+1阶段,与第k+1阶段物品一起按Step 2至Step 4过程进行装箱,计算转入物品需分摊的箱子成本,加上对应的延迟交付成本得到转入成本Ck2.

Step 7若Ck1≤CK2,则剩余物品在本阶段装载,将Ck1计入第k阶段总成本;若Ck1≥Ck2,则剩余物品在第k+1阶段装载,相关成本计入第k+1阶段.

Step 8当k≤Nj时,令k=k+1,基于Step 6、Step 7考虑是否有物品加入,确定阶段总待装物品,按Step 2至Step 7进行新阶段物品装箱.

Step 9当k=Nj时,将各阶段装箱计划相加得到的完整的装载方案,作为问题初始解输出.

3.2 解的改进

不同的物品序列形成不同的装载条件,并产生不同的装载效果,因此可通过改变物品的装载序列来获得不同的解.下面基于物品分值更新机制对各阶段物品序列进行调整,以实现物品在箱子间重新分配及最优解搜索的目的.

算法2初始解优化过程.

Step 1设k代表第k阶段装箱,Bk是初始解中第k阶段使用的箱子集,代表装载率较高的箱子,b(i)为物品i所在的箱子;设以装载率排序的箱子序列为(1,2,…,|Bk|),取B′k=另设n为第n轮更新,并设迭代产生的最优目标函数值为ZM,初始值为Z0.

Step 2令n=1,k=1,p=1,r=1按公式si=与)对物品的分值进行修改,其中m为分数修改的比例参数,¯s为分数修改的最大百分比,p为¯s的调节系数,r为物品发生位置交换的数量规模参数,pm、rm分别为p和r的最大值.

Step 3令k=k+1,转Step 1完成后续各阶段物品分数修改,由此确定新的各阶段物品装载序列,再按算法1重新进行装箱,并计算新方案的目标函数值Zn(n=1,…,ND).

Step 4当n≤ND时,令n=n+1进入新的搜索:若r＜rm时,令r=r+1,若r=rm时,重置r=1,按Step 1至Step 3确定装载方案,并计算新方案对应的目标函数值Zn;当n=ND时,转Step 6.

Step 5若Zn＞ZM令ZM=Zn,若Zn＜ZM则ZM不变,若Zn=ZM时令p=p+1;转Step 4.

Step 6将ZM对应的装载方案作为最终方案输出.

4 实例分析

假设某公司在当前获得了从8点至17点时段内8批次货物到达信息,且随时间的推移允许对时段内的到货信息进行更改;根据货物到达时间分布,将全部批次作业分为3个阶段,各阶段及批次包含的物品及相应的时间信息如表1所示;箱子和物品的类数及体积以随机方式生成:以[1,3]和[1,5]间随机生成的整数分别作为箱子和物品的类数,以[2,10]和[100,600]随机生成整数分别表示物品和箱子的容积(结果如表2所示);设有足够多的箱子可供使用,要求制定时段内的装箱计划使总成本最小.

表1 各装箱货物数量与到达、交付时间信息Table 1 The items'amount and arriving and delivering time

表2 物品及箱子体积Table 2 The sizes of items and bins

针对上述问题,先设定相关作业参数,如表3所示.再结合2.2中提到的三种信息条件下的模型,使用Delphi实现有关算法(HCA),在配置为英特尔2.9G双核处理器、2G内存电脑上运行,可较快计算出三种方式下的结果(如表4所示):第一种是静态信息条件,即为各个阶段独立制定装箱计划,计划时只掌握本阶段物品信息;第二种为理想信息条件,即计划时已获悉三个阶段物品信息,将三阶段结合到一起统一计划;第三种属于信息可实时更新的情况,它基于已有信息并通过引入权重α以滚动的形式制定出当前包含多阶段的整体装箱计划.

从计算结果中可看出,基于完全信息的整体优化求得的解,比基于静态信息且各阶段单独计划产生的解要好,这与实际情况相符合,而单独计划解的质量与阶段的划分有关;实时信息下制定多阶段计划可使用不同的权重α(α=0.3,α=0.6),即权重序列(1,α,α2,…,αK)对应不同的值,可得到不同的计算结果.α反映到达物品波动变化程度,它通过影响有可能进行阶段转移和装载的物品产生相应的作用,取值越大对波动越不敏感,而完全信息条件可视其为1.

由于涉及多个阶段装箱问题的研究甚少,相关实例及对比研究也比较缺乏,为了验证HCA算法的效果,结合文献[3]设计的实例及其使用的马尔科夫链-蒙特卡洛算法(MCMC)实施结果,进一步针对单阶段T-VS-BPP运用本文方法来求解.为适应对比需要,将算法中物品体积属性改为重量形式;同时采取和文献[3]相同的分布随机生成物品重量及单位延迟成本,箱子的体积、处理时间和物品的数量、滞留成本等参数设置也与其相同,大箱子可用数为0.25 N,小箱子可用数为0.5 N;并将算法中的阶段数Nj设为1.取20次运行的平均值为最终计算结果,实验对比如表5所示.表5中列举了6组不同数量的物品装载的实验结果,分别包括目标函数值、计算时间、大箱(RB)和小箱(RS)的使用比例.

表3 相关参数设定Table 3 The setting of parameters

表4 不同信息条件下的计算结果Table 4 The calculating results under different information conditions

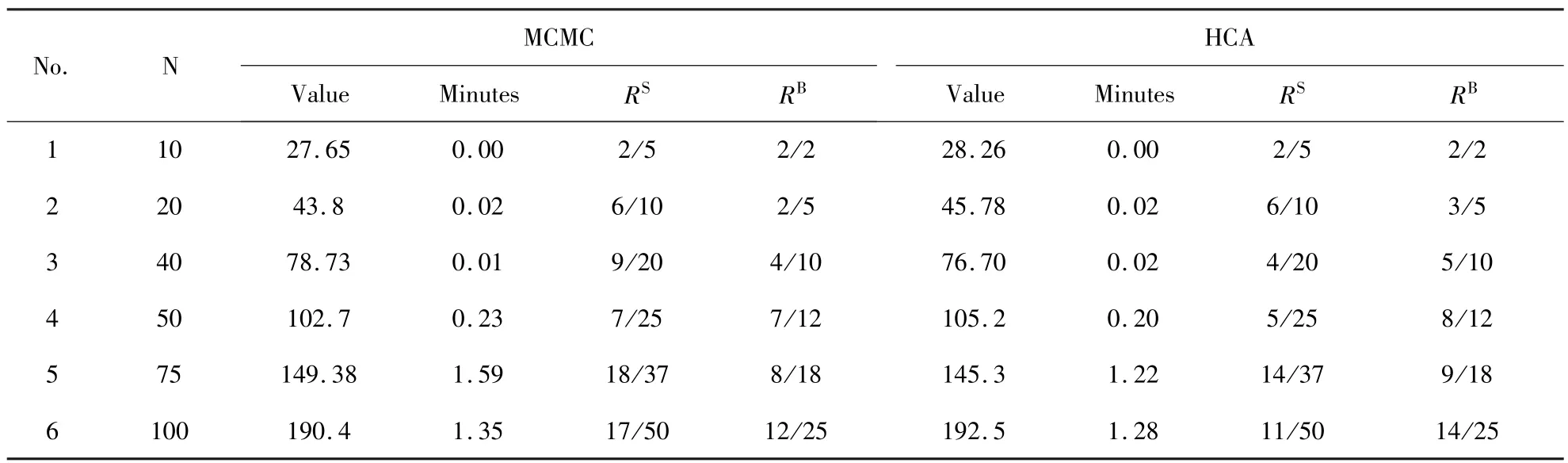
表5 HCA算法单阶段装箱求解效果Table 5 Performance of HCA for a single phase problem

通过对比可以看出,两种方法对应的目标函数值基本接近,但存在一定的差异,这主要和实验以随机方式生成有关属性参数有关;在计算效率上HCA基本优于MCMC,HCA所具有的自适应贪婪搜索特性[6]可加快搜索进程,特别是当问题规模较大时更为明显;从大小箱子使用情况来分析,两种方法都偏向使用大的箱子,而HCA尤为如此,这也与其搜索机制有关.由于多阶段问题求解是在单阶段问题求解的基础上,引入成本比较及迭代搜索过程来实现的,因而HCA在处理单阶段问题时的效果,可为其适应复杂的多阶段问题的求解提供较好的基础.

5 研究结论

多阶段带时间约束的VS-BPP考虑动态环境下变尺寸装箱优化问题,本文将一般带时间约束的VS-BPP置于多阶段研究框架,提出了基于确定信息的静态模型和基于滚动更新信息的动态模型;根据问题的特点设计了基于BFD规则与迭代松弛定界法相结合的构造算法进行求解;经实例运算和分析,证明方法能有效地对这一复杂动态问题进行求解.下一步可对订单取消、紧急插单等动态事件的作用机理进行研究,寻求适应动态复杂条件下装箱问题的算法也可作进一步拓展.

[1] Correia I,Gouveia L.Solving the variable size bin packing problem with discretized formulations[J].Computers and Operations Research,2006,35:2103-2113.

[2] Haouari M,Serairi M.Relaxations and exact solution of the variable sized bin packing problem[J].Comput Optim Appl,2011,48:345-368.

[3] Fazi S,Woensel T V.A stochastic variable size bin packing problem with time constraints[J].Working Papers Beta,2012(804):1-19..

[4] Yaman H,Sen A.Manufacturer's mixed pallet design problem[J].EuropeanJournalofOperational Research,2008,186:826-840.

[5] Polyakovskiy S,Hallah R M.An intelligent framework to on line bin packing[J],Lecture Notes in Computer Science,2011,6704:226-236.

[6] Crainic T G,Perboli G.Efficient lower bounds and heuristics for the variable cost and size bin packing problem[J].Computers&Operations Research,2011, 38:

1474-148 2.

Optimization of Multi-phase Variable Size Bin Packing Problem with Time Constraints

ZHU Xiang,LEI Ding-you,YOU Wei
(School of Traffic&Transport Engineering,Central South University,Changsha 410075,China)

The multi-phase variable size bin packing problem with time constraints originates from the variable size bin packing problem(VS-BPP)after being placed in dynamical environment.It requires formulating a proper schedule which can minimize the total bin and time cost through selecting the different bins to form a combination to packing items involving multi-phase and with tardiness date.It has complex and dynamical natures,and there have been a plenty of applications in reality.This paper investigates the VS-BPP with time constraints under the multi-phase framework.Then it develops a static model based on exacted information and a dynamic model with rolling updating.According to the characteristics of the problem,a heuristic constructive algorithm is presented integrating the best first decreasing rule and lower bounds technique.The numerical example demonstrates that the models and the algorithm perform well when solving the special bin packing problems.

logisticsengineering;dynamicoptimization;constructivealgorithm;VS-BPP; time constraints

U294.6

: A

U294.6

A

1009-6744(2013)04-0157-07

2013-03-04

2013-04-14录用日期:2013-04-26

国家自然科学基金资助项目(70971140).

朱向(1976-),男,湖南长沙人,博士生,讲师.

*通讯作者:cszhuxiang@163.com