有效应力下多孔介质微观结构的分形特征

李 玮，徐艳坤，闫 铁，王茂盛，张红卫

（1.东北石油大学 石油工程学院，黑龙江 大庆163318；2.大庆油田勘探开发研究院，黑龙江 大庆163712）

多孔介质广泛分布在地壳的浅层及深层，如地表的土壤、深层的岩石等。在结构上是由相互连接的固体颗粒和颗粒间的孔隙组成。多孔介质微观结构的复杂性、非均质性受到国内外学者的广泛研究，研究发现孔隙结构的空间分布具有统计自相似性。Pfeifer等首先用分子吸附法研究了多孔介质的孔隙结构，并得出其微观结构具有分形性的结论［1］。Katz等利用扫描电镜（SEM）对不同类型的砂岩进行研究，结果表明砂岩孔隙空间具有分形特征［2］。Friesen等用压汞仪测试了煤的孔隙结构，并根据测试得到的毛管压力数据计算了煤颗粒分布的分形维数［3］。

通常情况下，多孔介质会受到外部应力和内部应力的共同作用，其自身的微观孔隙结构在有效应力作用下发生变化。这种变化直接影响孔隙介质的大小、形状、分布、孔隙度和渗透率等。Terzaghi首先研究了多孔介质骨架中有效应力和孔隙中流体压力对总应力的分配问题，给出了经典的有效应力原理［4］。为了更好地解释多孔介质自身结构与有效应力之间的关系，少数学者提出了对Terzaghi方程的修正［5－8］。黄远智等研究了不同岩样的渗透率随有效压力的变化规律，并给出有效围压与岩样渗透率关系的经验公式［9］。郑玲丽等研究发现有效应力系数与围压和孔隙流体压力有关，且表现出明显的非线性特征［10］。本文以分形几何理论为基础，通过建立有效应力的分形计算模型，计算分析和讨论多孔介质微观结构和有效应力之间的关系，从微观角度上揭示有效应力对多孔介质孔隙结构的影响规律。

1 多孔介质有效应力的分形计算模型

根据分形几何理论，在DT维的欧式空间中存在一个多孔介质，则多孔介质中孔隙直径r和累积数目N（r＜L）存在幂律关系［11］

式中：C1为常数；L为物体大小；Df为分形维数。

若孔隙直径的最大和最小值分别为rmax和rmin，可得到多孔介质中孔隙度φ［12］

在多孔介质中任取一单元截面（图1）。其截面边长为l，在该截面上对多孔介质施加一总应力σOV，若固体颗粒上的基岩应力为σ，则根据受力平衡有

图1 多孔介质中各应力之间的关系图Fig.1 The relation figure of all stresses in porous media

式中：A为孔隙和固体颗粒的总截面积，A＝l2；A1为岩石颗粒接触面积；A2为截面上孔隙的面积；且A＝A1＋A2；pp为孔隙压力。

对于所选单元截面的孔隙度为

将式（4）带入式（3）可得

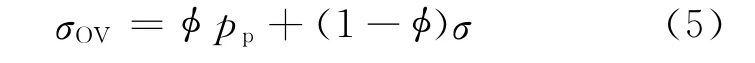
将式（2）带入式（5）得

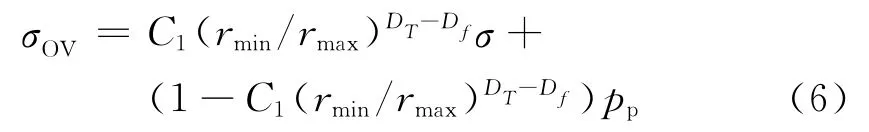
上式为多孔介质有效应力的分形计算模型。由模型中参数可知，应力环境会改变多孔介质的孔隙大小及孔隙结构分布的分形维数。

2 有效应力下孔隙大小分布的分形模型

在三轴应力σ1、σ2和σ3作用下的多孔介质发生变形，其体积应变为

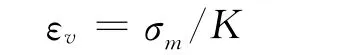
式中：σm＝ （σ1＋σ2＋σ3）／3；K 为体积模量。

三轴应力条件下多孔介质变形后孔隙大小为

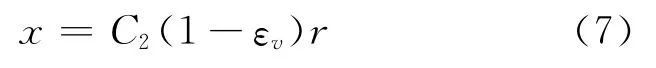
式中：C2为系数。

对平面应力条件，εz＝0，σz＝0，σx＝σy，其应变为

由广义胡克定律和式（5）可知

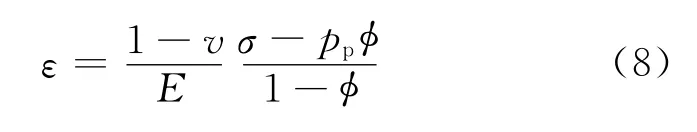
平面应力条件下多孔介质变形后孔隙大小为

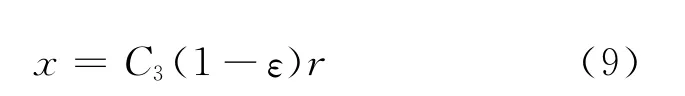
式中：C3为系数。

变形后的多孔介质孔隙微观结构分布依然是分形。以平面应力条件为例，由此式（1）形式变为

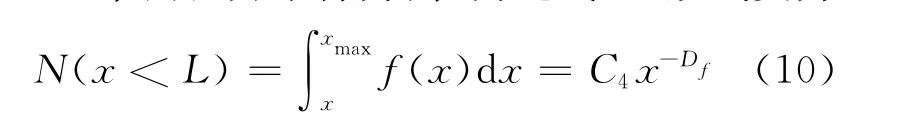
式中：C4为系数；Df为变形后孔隙微观结构分布的分形维数。

根据式（10），单位体积多孔介质中存在的孔洞总数为

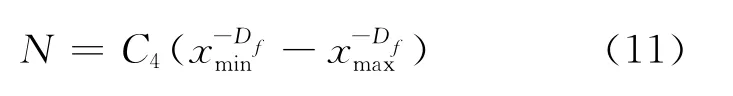
考虑多孔介质孔隙大小是连续分布的，将式（10）对x求导，可得到孔隙大小分布的密度函数f（x）的表达式

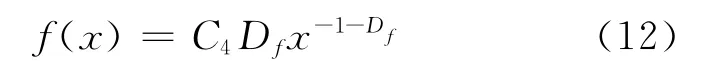
由此可得多孔介质中孔隙的平均半径

多孔介质的总孔隙体积为

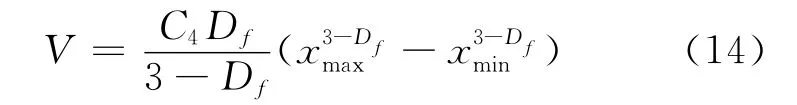
3 分析与讨论

在有效应力作用下，多孔介质的孔隙大小及其分布分形维数会发生变化。如式（7）和式（9）分别给出了三轴应力条件下和平面应力条件下多孔介质孔隙大小变形的关系式。式（8）中多孔介质的变形量中存在孔隙度结构参数，这说明多孔介质在有效应力作用下的变形是耦合过程。

由式（6）可得

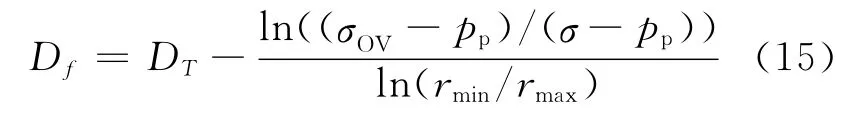
由式（15）可知，随着有效应力的增大，孔隙的最大尺寸和最小尺寸变小，大小分布的分形维数将发生变化。

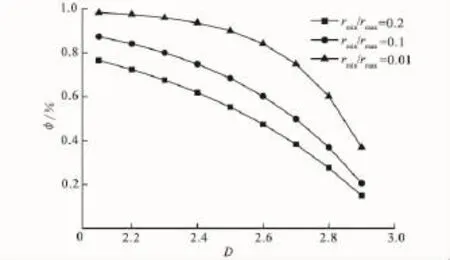
图2 孔隙度和分形维数之间的关系Fig.2 The relationship between porosity and fractal dimension

根据式（2）可以绘制不同孔隙大小比值下孔隙度和分形维数之间的关系。图2表明，在一定的分形维数下，rmin／rmax比值越小，孔隙度越大；不同rmin／rmax比值孔隙度随着分形维数呈指数递减。当Df→3，多孔介质被固体充满，孔隙完全闭合。Fripiat［13］在分析多孔介质孔隙率与等温吸附分形时，得到了当Df＝3时孔隙度为零的结论。由式（15）绘制图3，可知作用在多孔介质上的有效应力增大，分形维数Df→3，由图2知孔隙度呈φ→0。Pfreifer认为不规则的无序的多孔介质在Df→3时，其孔隙度不等于零［14］。作者认为，式（6）虽可直接用于分析有效应力对多孔介质孔隙分形维数的影响分析，但Df→3，只是σ→∞时才会出现。刘俊亮等的研究［15］表明，多孔介质孔隙率应表现为Df的减函数而非增函数，对于rmin／rmax≠0的无序的多孔介质，其孔隙度将微偏离严格固相分形体模型。

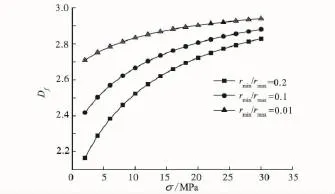
图3 有效应力和分形维数之间的关系Fig.3 The relationship between effective stress and fractal dimension

Louis给出有效应力和孔隙之间的关系式［16］，即指数型数学模型

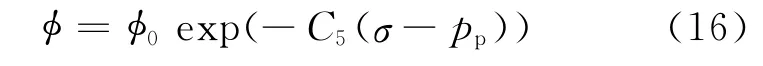
式中：φ0为初始孔隙度；C5为压实系数。

随着地层深度的增加，作用在多孔介质上的有效应力增大，其孔隙度呈指数递减趋势。式（15）分析结果与压实规律相符。文献［1，16］的试验表明，随着有效应力的增加，多孔介质的孔隙度和渗透率呈不同程度的下降。

图4 有效应力对总孔隙数的影响Fig.4 The influence of effective stress on the total pore number

由式（11）可以绘制图4。图4表明随着有效应力的增大，孔隙数呈指数递减趋势，且N→0，rmin／rmax比值越大，孔隙大小分布区间越小，总孔隙数越少。

由式（13）绘制图5。显然，有效应力增大，孔隙闭合，孔隙平均尺寸变小。当rmin→0，整个多孔介质被固体充满，而孔隙度φ→0。

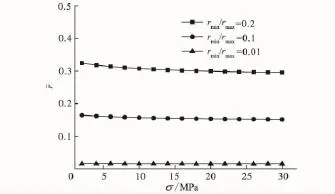
图5 有效应力对平均孔隙大小的影响Fig.5 The influence of effective stress on the average pore size

4 结论

a.建立了多孔介质有效应力的分形计算模型，由该模型可分析有效应力对多孔介质孔隙大小及孔隙结构分布分形维数的影响。

b.根据有效应力的分形计算模型可知，随着有效应力的增大，多孔介质的分形维数呈指数增加，孔隙度呈指数递减，且分形维数Df→3，孔隙度呈φ→0。

c.随着有效应力的增大，多孔介质中孔隙数呈指数递减趋势，且N→0，rmin／rmax比值越大，孔隙大小分布区间越小，总孔隙数越少。

d.随有效应力增大，孔隙平均直径呈减小趋势。当rmin→0，整个多孔介质被固体充满，而孔隙度φ→0。

［1］Pfeifer P，Avnir D.Chemistry in nonintegral dimensions between two and three：I：Fractal theory of heterogeneous［J］.Journal Chemical Physics，1983，79（7）：3369－3558.

［2］Katz，A J，Thompson A H.Fractal sandstone pores：implications for conductivity and pore formation［J］.Phys Rev Lett，1985，54：1325－1328.

［3］Friesen，W I，Mikula R J.Fractal dimensions of coal particles［J］.Journal of Colloid and Interface Science，1987，120（1）：263－271.

［4］Terzaghi K.Principle of soil mechanics［J］.Engineering News Record，1925，95：832－836.

［5］Zimmermam R W，Somerton W H，King M S.Compressibility of porous rocks［J］.Journal of Geophysical Research，1986，91（B12）：765－777.

［6］Lade P V，De Boer R.The concept of effective stress for soil，concrete and rock［J］.Géotechnique，1997，47（1）：61－78.

［7］李传亮.多孔介质应力关系方程［J］.应用基础与工程科学学报，1998，6（2）：145－148.Li C L.A new equation of stresses in porous media［J］.Journal of Basic Science and Engineering，1998，6（2）：145－148.（In Chinese）

［8］闫铁，李玮，毕雪亮.基于分形方法的多孔介质有效应力模型研究［J］.岩土力学，2010，31（8）：2626－2630.Yan T，Li W，Bi X L.Research on effective stress model in porous media based on fractal method［J］.Rock and Soil Mechanics，2010，31（8）：2626－2630.（In Chinese）

［9］黄远智，王恩志.低渗透岩石渗透率与有效围压关系的实验研究［J］.清华大学学报：自然科学版，2007，47（3）：340－343.Huang Y Z，Wang E Z.Experimental study of the laws between the effective confirming pressure and rock permeability［J］.Journal of Tsinghua University（Sci ＆ Tech），2007，47（3）：340－343.（In Chi－nese）

［10］郑玲丽，李闽，钟水清，等.变围压循环下低渗透致密砂岩有效应力方程研究［J］.石油学报，2009，30（4）：588－592.Zheng L L，Li M，Zhong S Q，et al.Research on calculation of effective stress in low－permeability sandstone rock under cyclic loading and unloading［J］.Acta Petrolei Sinica，2009，30（4）：588－592.（In Chinese）

［11］Mandelbrot B B.The fractal geometry of nature［M］.San Francisco：W.H.Freeman and Company，1982.

［12］Yu B M，Li J H.Some fractal characters of porous media［J］.Fractal，2001，9（3）：365－372.

［13］Fripiat J J，Avnir D.The Fractal Approach to Heterogeneous Chemistry：Surfaces，Colloids，Polymers［M］.New York：John Wiley ＆ Son Ltd，1989.

［14］Pfeifer P，Unger K K.The Third IUPAC Symposium on the Characterization of Porous Solids［M］.Elsevier，1987.

［15］刘俊亮，田长安，曾燕伟，等.分形多孔介质孔隙微结构参数与渗透率的分维关系［J］.水科学进展，2006，17（6）：812－817.Liu J L，Tian C A，Zeng Y L，et al.Fractal dimensionality dependence of microstructural parameters and permeability in fractal porous media ［J］.Advances in Water Science，2006，17（6）：812－817.（In Chinese）

［16］肖文联，李闽，赵金洲，等.低渗致密砂岩渗透率应力敏感性试验研究［J］.岩土力学，2010，31（3）：775－780.Xiao W L，Li M，Zhao J Z，et al.Laboratory study of stress sensitivity to permeability in tight sandstone［J］.Rock and Soil Mechanics，2010，31（3）：775－780.（In Chinese）