基于ANSYS 的某圆锥破碎机主要部件的静力分析

尚思思，张园园，张巨伟

（辽宁石油化工大学，辽宁 抚顺113001）

破碎机是一种将物料破碎到一定颗粒的重型设备，在冶金、矿山、化工、电力等工业部门广泛应用。在化工部门，破碎粉磨机械将原料破碎粉磨，增加物料的表面积，为缩短物料化学反应的时间创造了有利条件。主轴、动锥及其衬板是某圆锥破碎机的关键部件，其设计参数的选择与确定直接影响圆锥破碎机的使用寿命和可靠性。同时，破碎机在正常的工作过程中，由于动锥衬板与物料直接接触[1]，衬板的上载荷情况极为复杂，难于求解，一般的设计部门对其研究的较少或只停留在理论分析阶段，因此本文将采用有限元法对三者进行静力学分析，较为准确的计算出应力分布情况，为该类圆锥破碎机主要部件的设计提供有价值的参考数据。

1 实体模型的建立

圆锥破碎机的主轴、动锥以及动锥衬板在工作过程中是相互接触配合的，并且主轴和动锥的受力都是来源于动锥衬板破碎物料时受到的破碎力。因此，本文将通过动锥衬板受到的破碎力以及部件的相互作用力，来对各部件的受力情况进行求解。

2 ANSYS 分析设定

2.1 定义单元属性

结合被分析零件结构和应变特点，选用Solid45单元；选用的材料是各项同性的线弹性材料。

2.2 网格的划分

本论文采用扫掠的方法生成网格[2,3]。首先将源面统一确定为各部件的左剖面，先将源面划分成25×25 的四边形网格，并对各个部件的圆角处进行细化处理。在扫掠方向上统一设置的单元划分数量为35，对部件进行扫掠划分。

2.3 施加约束和载荷

2.3.1 施加约束

本文根据圆锥破碎机工作的实际情况，对主轴的两端面进行全位移约束，在动锥螺母和塑胶背垫的顶部表面施加Y 方向的位移约束，在各部件的剖分面的处施加对称位移约束，并在切割环与动锥螺母和动锥衬板的接触处施加全位移耦合约束。

2.3.2 载荷计算及施加

(1) 沿动锥衬板垂直方向上的单位破碎力。H.Sommer 认为：垂直动锥衬板的表面上，任意截面的单位破碎力，与其对应的偏心距 成正比，与破碎腔宽度 成反比[4]，由此可得垂直方向上单位破碎力：

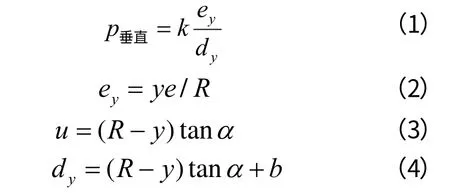
将式(2)和式(3)带入(1)中，可得出单位破碎力的表达式为：

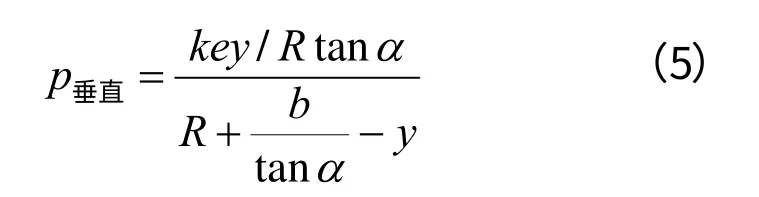
(2) 沿动锥衬板圆周方向上的单位破碎力。动锥衬板的外形类似于圆锥形，它在实际工作过程中大约只有1/4 的圆周在进行破碎，即只有-45°～45°的范围为工作区，并且受力由工作区中间部位即0°处沿着圆周方向两侧递减，一直到两侧的-45°和45°位置处破碎力已经减小了非常多，几乎为0 MPa，设单位破碎力沿圆周方向上递减的曲线为抛物线。

（3) 作用在动锥衬板工作区的单位破碎力。根据式(1)和式(5)可求得动锥衬板工作区的单位破碎力为：

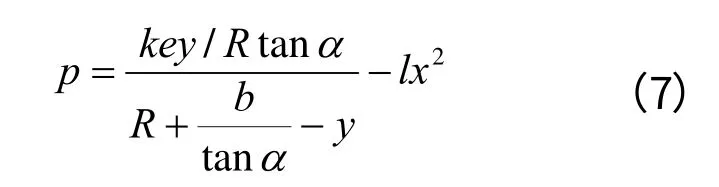
求解式(7)中的未知数 ：本文将衬板由上至下分成 10 份（ 已知），由于动锥衬板的工作区 处（ 已知）的单位破碎力为0 MPa（ 已知），分别在每一段根据式(7)算出，带回到(7)式中，即可求得单位破碎力函数 。由于单位破碎力是随着 坐标变化的函数，因此需要使用ANSYS 软件的函数编辑器功能进行加载[5]。

2.4 定义接触

本文使用接触向导创建所需的三对接触。第一对接触主轴表面作为接触面，将与其接触的动锥的内表面和螺母的内表面作为目标面；第二对接触将动锥的外表面作为接触面，与其接触的塑胶背垫和衬板的内表面作为目标面；第三对接触将塑胶背垫的外表面作为接触面，与其接触的衬板内表面作为目标面[6]。

3 计算结果

3.1 主轴的计算结果及分析

由图1 可知，主轴的最大等效应力值为112.174 MPa，在主轴与动锥螺母接触的圆角处，由于该处圆角的尺寸较小且单元网格的划分无法足够的精确，与实际模型相比会有一定的差距，因此产生了应力集中。主轴中部与动锥相接处的位置上的应力值也很大，呈两条带状分布在剖分边缘的附近，相比之下，主轴其它部位的应力很小。由图2 可知，主轴的最大位移出现在轴的中部，轴的两端由于受到约束，几乎没有产生位移。

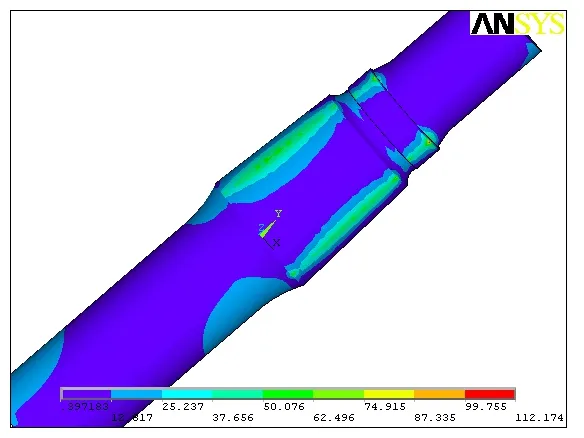
图1 主轴的应力分布云图Fig.1 Spindle stress contours

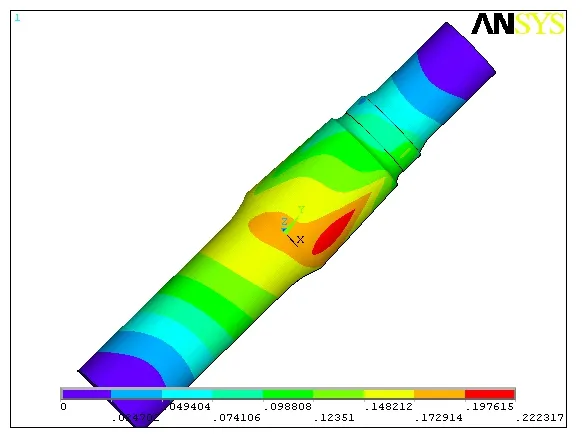
图2 主轴的位移分布云图Fig.2 The displacement contours of spindle

3.2 动锥的计算结果及分析

由图 3、4 可知，动锥的最大等效应力值为118.482 MPa，在动锥内壁和外壁间的圆角处，这是由于外壁受到了来自衬板的挤压产生变形，于是在该处形成了应力集中。

图3 动锥的应力分布云图(a)Fig.3 The stress contours of moving cone(a)

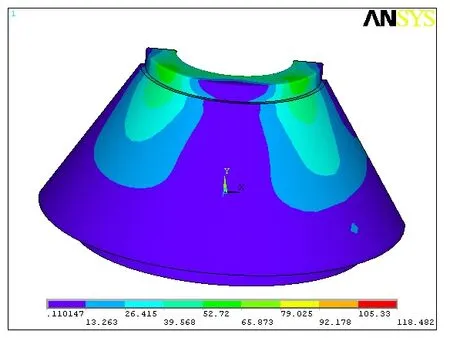
图4 动锥的应力分布云图(b)Fig.4 The stress contours of moving cone(b)

此外，动锥与主轴接触的内表面上的应力值也很大，主要分布在动锥的上下边缘附近，动锥外壁的边缘处应力则很小。由图5、6 可知，动锥有两处较大的位移，一处出现在动锥的外壁的边缘处，另一处出现在动锥的内壁下边缘处。

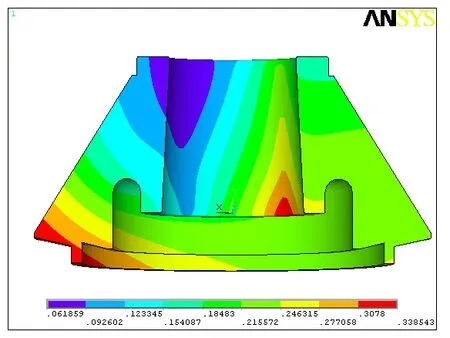
图5 动锥的位移分布云图(a)Fig.5 The displacement contours of moving cone(a)

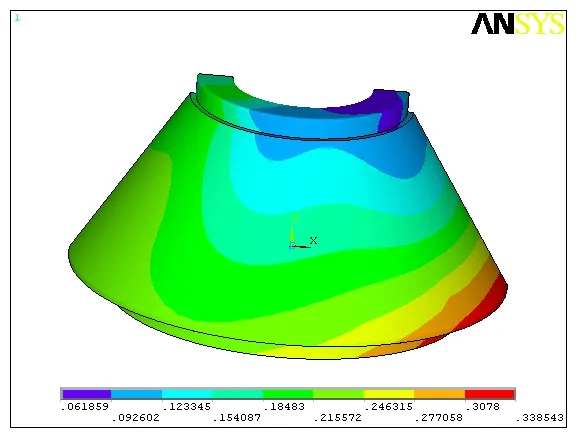
图6 动锥的位移分布云图(b)Fig.6 The displacement contours of moving cone(b)

3.3 动锥衬板的计算结果及分析

由图7、8 可知，动锥衬板的最大等效应力值为57.552 MPa，发生在动锥衬板的内表面下边缘处。此外，动锥衬板与矿石直接接触的外表面应力值也很大，主要分布在衬板破碎区域的下边缘附近，非破碎区域的应力则很小。

由图9 可知，动锥衬板的最大位移出现在衬板下边缘，主要是由于衬板的一侧受到挤压后产生弯曲而形成的。

图7 动锥衬板应力分布云图(a)Fig.7 The stress contours of dynamic cone lining(a)

图8 动锥衬板应力分布云图(b)Fig.8 The stress contours of dynamic cone lining(b)

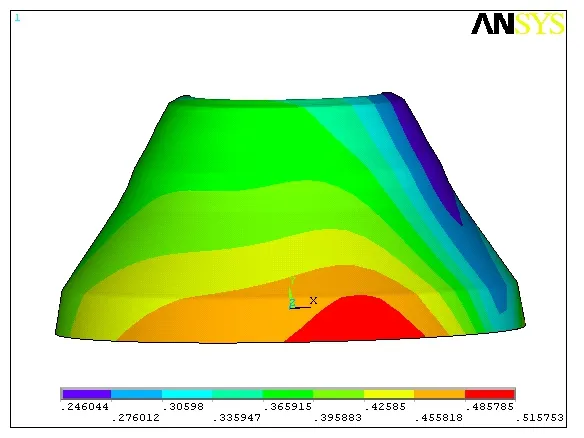
图9 动锥衬板的位移分布云图Fig.9 The displacement contours of dynamic cone lining

4 结 论

关键部件非线性静力有限元分析的结果表明：

(1)主轴的最大等效应力出现在主轴与动锥螺母接触的圆角处，为112.174 MPa，是由应力集中引起的，主轴的最大位移出现在轴的中部。

(2)动锥的最大等效应力出现在动锥内壁和外壁间的圆角处，为118.482 MPa。动锥的最大位移一处出现在动锥外壁的边缘，另一处出现在动锥内壁下边缘。

(3)动锥衬板的最大等效应力出现在动锥衬板内表面的下边缘，为 57.552 MPa。最大位移出现在衬板下边缘，主要是由于衬板的一侧受到挤压后产生弯曲而造成的。此外，在主轴中部靠近剖分边缘的位置，在动锥内表面的上下边缘的附近，在动锥衬板外表面的下半部的应力值也很大。

［1］李显忍.圆锥破碎机定锥修复[J].化工机械，2001，28(6)：355-356.

［2］叶先磊，史亚杰. ANSYS 工程分析软件应用实例[M].北京：清华大学出版社，2003:63-66.

［3］袁国勇. ANSYS 网格划分方法的分析[J].现代机械，2009(6)：59-60.

［4］郎世平,郎宝贤. 破碎机[M].北京：冶金工业出版社，2008:112-113.

［5］刘扬，刘巨保，罗敏. 有限元分析及应用[M].北京：中国电力出版社，2008:177-178.

［6］苏荣华，梁冰. 结构仿真分析 ANSYS 应用[M].沈阳：东北大学出版社，2005:185-186.