基于ABAQUS的钢筋混凝土结构悬臂梁跨高比的分析研究
黄 辉,陈 韦,彭杰波,黄 丹,廖文远
(1.长沙理工大学土木与建筑学院,湖南长沙410114;2.江苏省张家港市建筑设计研究院有限责任公司保税区分公司,江苏张家港215600;3.华南理工大学土木与交通学院,广东广州510640;4.昆明理工大学建筑工程学院,云南昆明650504)
1 工程实例
钢筋混凝土悬臂梁结构可以使建筑体型独特、外观新颖、增加有效的上部利用空间。在实际工程中应用广泛,多用于挑檐、阳台、雨棚以及屋顶等。
中元·铂金湾幼儿园如图1所示,地处云南保山,属三层公共建筑。抗震设防烈度八度,耐久年限为3类,耐火等级为二类,屋面防水等级为Ⅲ级。铂金湾幼儿园利用钢筋混凝土悬臂梁结构使建筑的室内空间得以延伸,提高内外部空间的联系。幼儿园是让幼儿身体、智力和心情健康发展的场所,因其特殊性,幼儿园的建筑结构设计要求更高,比如还需满足《混凝土结构设计规范》(GB 50010-2010)[1]中对托儿所、幼儿园设计的各项要求。

图1 中元·铂金湾幼儿园效果图
钢筋混凝土悬臂梁结构设计的关键是跨高比的取值,现阶段对于跨高比的取值规范没有明确的规定,往往是通过经验取值,因此在工程实际设计过程中跨高比的取值成为研究的热点。文献[2]及文献[3]给出了在不同荷载集度下,集中荷载作用下钢筋混凝土悬臂梁h/b=2~3的容许跨高比上下限值。本文运用ABAQUS非线性分析软件以及规范规定的裂缝宽度计算公式,对悬臂梁在不同跨高比下的受力、挠度及裂缝宽度分析对比。铂金湾幼儿园结构平面图如图2所示。

图2 幼儿园结构平面图
2 本构关系
2.1 计算模型的选取
混凝土采用 ABAQUS 软件中的损伤塑性模型[4]、[5],该模型可用于单向加载、动态加载及循环加载等情况,具有较好的收敛性。采用各向同性损伤弹性结合压缩塑性和各向同性拉伸的模式来表示混凝土的非弹性行为。钢筋采用ABAQUS软件中的等向强化弹塑性模型[6],满足 VonMises屈服准则。
2.2 现行规范的有关规定
在工程实践中结构物的裂缝形成产生的原因可分为两类,一类是由荷载引起的裂缝,另一类是由变形因素(非荷载)引起的。由于本文中提到的跨高比上、下限值是通过《混凝土结构设计规范》中的最大裂缝宽度限值计算的,为了使多组跨高下裂缝宽度和最大裂缝宽度限值具有可比性,本模型采用《混凝土结构设计规范》(GB 50010-2010)中公式:

3 计算实例
3.1 计算简图
根据建筑物结构图(如图2),本栋最大悬挑长度2.5 m,经受力分析,等效于悬臂端集中荷载P=5 000 N,计算简图如图3。集中荷载作用下钢筋混凝土悬臂梁h/b=2~3的容许跨高比限值如表1。当集中荷载作用下钢筋混凝土悬臂梁h/b=2、(Gk+Qk)/l2≤2情况,跨高比上限取8.3~8.7,下限取5.9~6.8,用ABAQUS软件对本例悬臂梁模拟分析,选用限值范围内的四组跨高比5、6、7、8进行比较,分析不同跨高比下结构的受力、挠度及裂缝宽度,并分析原因(考虑跨高比为单一变量定宽高比h/b=2,箍筋采用沿梁全长加密)。

图3 梁配筋示意
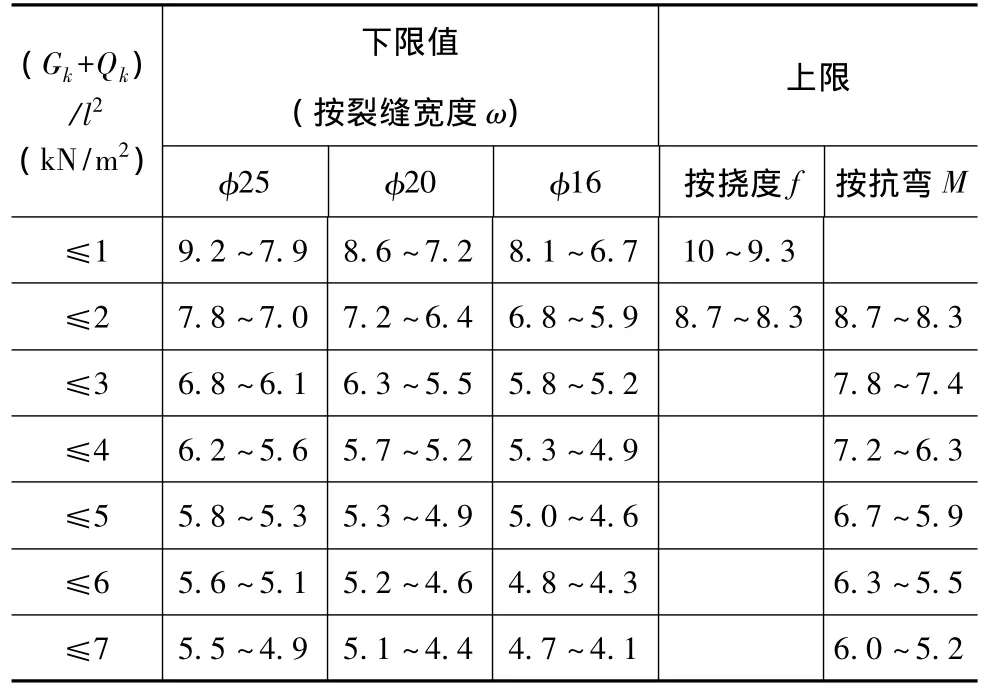
表1 集中荷载作用下钢筋混凝土悬臂梁h/b=2~3的容许跨高比上下限值
混凝土采用C30,受力钢筋、箍筋均选用HRB335,保护层厚度取C=35 mm,梁截面尺寸如图3所示,混凝土、钢筋特性及跨高比分组数据分别如表2~表4所示。

表2 混凝土特性

表3 钢筋特性

表4 跨高比分组数据
3.2 ABAQUS有限元模型的建立
本文用非线性有限元分析软件ABAQUS建立钢筋混凝土悬臂梁的三维有限元模型[7]、[8]。钢筋混凝土结构的有限元模型有三种建模方式,分别是整体式模型、界面单元分离式模型和位移协调分离式模型。整体式是假定混凝土和钢筋粘结很好,且将单元看作连续均匀材料,因此只需用混凝土单元模型,把钢筋分布于整个单元中。界面单元分离式模型就是把混凝土、钢筋用不同单元处理,并用弹簧单元连接,来模拟钢筋与混凝土之间的滑移,这种建模方式能逼真的模拟钢筋混凝土的实验力学行为,但是建模难度大,且工作量大。位移协调分离式模型是将钢筋与混凝土用不同单元来处理,并将钢筋和混凝土固结在一起,忽略两者之间的相对滑移,实验表明当保护层厚度足够时,设置剪切连接键,滑移不是问题。本文结合工程实例采用位移协调分离式方法建模。
在ABAQUS中,混凝土结构中的钢筋可以通过钢筋单元来实现,可以添加单独的钢筋单元,也可以在单元属性中附加钢筋属性以组合模型的钢筋,还可以通过Embed[9]方法将链杆单元或者模单元嵌入混凝土单元,Embed可以把钢筋和主体构件分别显示,方便对钢筋性能的考察,本文采用Embed方法将钢筋单元嵌入混凝土单元。
混凝土采用8节点六面体线性减缩积分的三维实体单元C3D8R,该单元计算效率高且不易发生剪切自锁;钢筋采用三维二节点线性桁架单元T3D2,此单元每个节点有水平和垂直两个自由度,最终建立的悬臂梁有限单元如图4所示。

图4 悬臂梁单元图
3.3 模拟结果及分析
本工程选用限值范围内的四组跨高比进行比较,利用ABAQUS非线性软件绘制出集中荷载作用下,四组跨高比作用下悬臂梁的应力、位移云图如图5~图7。根据云图绘制梁内混凝土最大应力、钢筋最大应力、最大挠度曲线如图8、图9。
各曲线图表明,混凝土、钢筋应力与挠度都随着跨高比的增大而减小,比如跨高比为5~8时,混凝土的应力最大分别对应为 1.05×106Pa、1.66×106Pa、2.59×106Pa、4.84×106Pa。由《混凝土结构设计原理》[10]可知,钢筋混凝土悬臂梁的正截面承载能力与梁截面的高度成正比,最有效提高钢筋混凝土悬臂梁的正截面承载力的措施就是增大梁高,比增大配筋、提高混凝土强度更加有效。
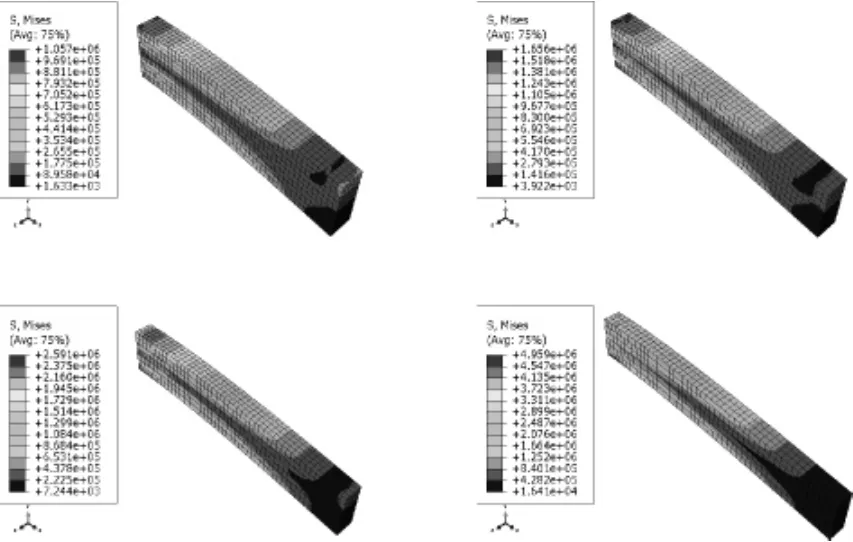
图5 l/h=5~8混凝土的应力云图
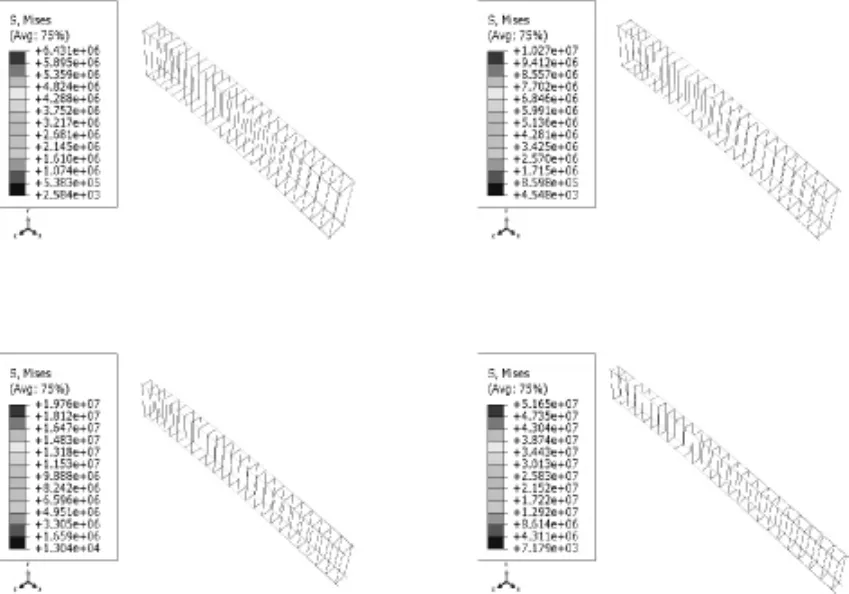
图6 l/h=5~8钢筋的应力云图

图7 l/h=5~8悬臂梁的位移云图
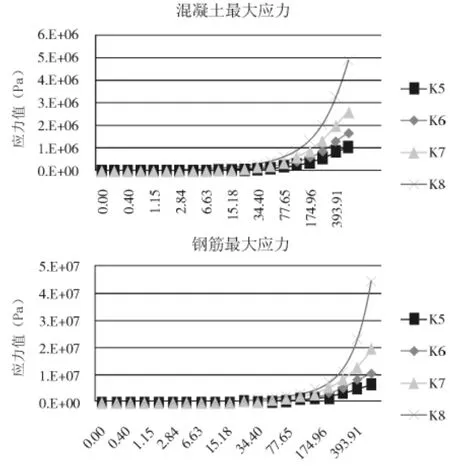
图8 混凝土、钢筋最大应力

图9 最大挠度图

图10 裂缝宽度变化曲线

表5 各跨高比下悬臂梁的最大裂缝宽度
由规范公式可知,在各跨高比下的裂缝宽度如表5,并绘制裂缝宽度变化曲线如图10。图中曲线表明当跨高比取6时,悬臂梁的最大裂缝宽度最小,这是由于跨高比的增大,虽然提高了截面刚度和强度,但是混凝土的自重也是我们在设计时需要考虑的因素。跨高比取值过大,会增大自重,使得混凝土自重成为最主要的荷载来源(表4中的自重);而跨高比取值过小时,刚度不够,也可能使裂缝增大。
根据各类性能曲线图与裂缝宽度表绘制出规范限值表如表6。由表可知最大裂缝宽度限值、混凝土、钢筋最大应力与最大挠度都是满足《规范》限值,说明文献提供的跨高比限值是合理的。

表6 规范限值满足情况
根据表6,规范限值采用的跨高比也仅仅只是一个范围,设计时要根据分析计算结合裂缝的控制等级,在范围内确定 最佳跨高比。本例对钢筋混凝土悬臂梁受力、位移及使用性能综合考虑,最终选定跨高比为6,即b=210 mm,h=420 mm。
4 结论
通过改变悬臂梁跨高比,分析其各项性能,从而选定悬臂梁梁截面,可以得出以下结论:
钢筋混凝土悬臂梁的跨高比对结构有很大的影响,跨高比取值过小,会使得正截面抗弯能力和挠度满足不了要求;取值过大,不仅自重大、造价高,而且使得裂缝宽度满足不了要求。在集中荷载作用下,存在跨高比上、下限值,使得悬臂梁抗弯、挠度及抗裂验算满足规范规定。
若设计中为了满足受力、挠度验算,一味增加梁高,不进行裂缝宽度验算是不合理的。
最佳跨高比的选择,除了满足受力、挠度及裂缝宽度规范限值之外,还要结合实际情况,比如建筑的裂缝控制等级、材料控制等等。
以上结论都是在假定钢筋混凝土悬臂梁结构是按“强剪弱弯”设计,且有一个理想的固定端,支座处无竖向位移、转角,在实际工程中,这些条件是否满足尚需注意。
[1]GB50010-2010混凝土结构设计规范[S]
[2]林云云,蒋大骅.钢筋砼悬臂梁的跨高比[J].建筑结构,1993(1):27-31
[3]Wen-zhong ZHENG,Xiao-dong WANG.Ultimatestress increase in unbounded tendons in prestressed concre tebeams[J].Journal of Zhejiang University-SCIENCE A(Applied Physics&Engineerin g),2010,11(12):998-1014
[4]石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2010
[5]雷拓,钱江,刘成清.混凝土损伤塑性模型应用研究[J].结构工程师,2008,24(2):22-27
[6]张伟,伍鹤皋,苏凯.ABAQUS在大体积钢筋混凝土非线性有限元分析中的应用评述[J].水力发电学报,2005,24(5):70-74
[7]胥玉详,朱玉华,赵昕,等.双连梁受力性能研究[J].结构工程师,2010,26(3):31-37
[8]Xiangting Su,Zhengjun Yang,Guohua Liu.FINITE ELEMENT MODELLING OF COMPLEX 3DSTATIC AND DYNAMIC CRACK PROPAGATION BY EMBEDDING COHESIVE ELEMENTS IN ABAQUS[J].Acta Mechanica Solida Sinica,2010,23(3):271-282
[9]刘林林,屠永清,叶英华.基于ABAQUS的钢管混凝土L形柱有限元分析[J]. 沈阳工业大学学报,2011,33(3):349-354
[10]沈蒲生.混凝土结构设计原理[M].北京:高等教育出版社,2007

