示值误差和测量不确定度在实验室认可中的应用

王学杰/上海通用东岳动力总成有限公司

0 引言

实验室资质认证评审准则ISO/IEC17025是实验室认可的纲领性文件，主要条款中，一方面是管理要求部分，另一部分是技术要求部分，其中检测校准方法和量值溯源是技术要求的核心。测量不确定度评定是解决检测校准方法和量值溯源是否符合ISO/IEC 17025标准要求的关键。

1 示值误差和测量不确定度

1.1 示值误差、最大允许误差的内涵

示值是指测量仪器所指示的被测量的值。示值概念具有广义性，既适用于指示式仪器装置标尺上所指示的量值，也适用于实物量具所标注的示值。

测量仪器示值与对应的输入量的真值之差称为示值误差。它是测量仪器的主要计量特性之一，本质上反映了测量仪器准确度的大小。

真值则为确定测量仪器的示值误差，使其接受高等级的测量标准器检定或校准时，标准器复现的量值即为约定真值（或校准值）。示值误差是对真值而言的，由于真值不能确定，实际上使用约定真值或实际值，则此时的示值误差为：示值误差=示值-实际值（校准值、标准值）

对于实物量具：示值误差=标称值-实际值

最大允许误差是对给定的测量仪器，由规范、规程等所允许的误差极限值。是在规定的参考条件下，测量仪器在技术标准、计量检定规程等技术规范中所规定的允许误差的极限值。可简称为最大允许误差，也可称为测量仪器的误差限。

1.2 示值误差和最大允许误差的区别

要区分测量仪器的示值误差和最大允许误差，两者都是对测量仪器本身来讲的；最大允许误差是指技术规范（如标准、检定规程）所规定的允许误差极限值，是一个判定是否合格的规定要求；而示值误差是测量仪器某一示值的误差的实际大小，是通过检定、校准所得到的一个值，可以评价测量仪器是否满足最大允许误差的要求，从而判断该测量仪器是否合格，或根据实际需要提供修正值，以提高测量结果的准确度。

图1给出了测量误差、随机误差和系统误差之间的关系。无限多次测量结果的算术平均值称为数学期望μ，只要测量次数n足够大，μ就是被测量Y的有限次数测量的算术平均值的无偏估计值，所以图中的平均值应该是与总体均值μ重合的。横坐标表示被测量Y的测量值，纵坐标表示被测量Y的概率密度，曲线是被测量的概率密度分布曲线。概率密度分布曲线与给定的横坐标的区间之间所包含的面积是测得值在该区间内出现的概率。

1.3 测量不确定度

测量不确定度是表征合理赋予被测量之值的分散性与测量结果相联系的参数。在测量结果的完整表述中，应包括测量不确定度。通俗地讲，测量不确定度是指测量结果变化不能肯定的程度，即可疑程度。表示被测量的测量结果在某个量值范围的一个估计，是测量结果含有的一个参数用来表示被测量值的分散性。

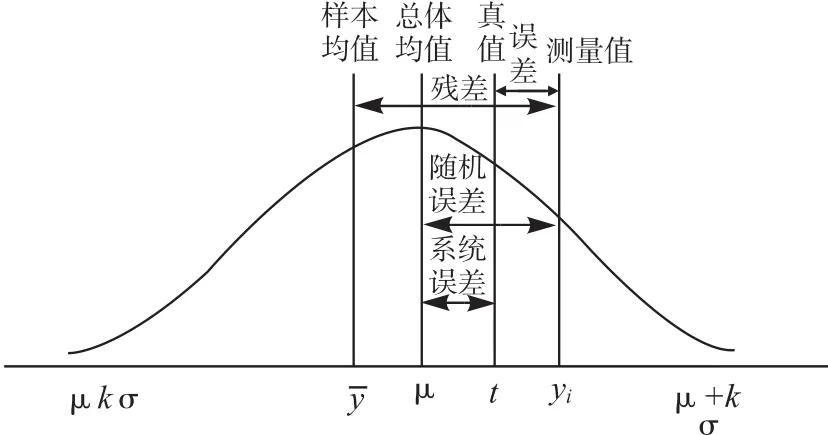
图1 测量误差、随机误差和系统误差的关系

1）不确定度是一个参数，也就是一种物理量。它不能独立存在，而是和测量结果一起存在，作为测量结果的一部分。

2）不确定度是表达分散性的一个量。

3）严格意义上讲，测量设备本身并无不确定度可言，但是在不确定度评定时往往要考虑上一级标准器具的不确定度和测量仪器本身示值误差造成的不确定度，这是指由于标准和仪器存在示值误差是测量不确定度的来源之一。

1.4 对误差和测量不确定度的理解

1）测量不确定度表明赋予被测量之值的分散性，是通过对测量过程的分析和评定得出来的一个区间，以估计值为中心；而测量误差是表明测量结果偏离真值的差值，以真值为中心。

2）经过修正的测量结果可能非常接近真值（误差很小），但是由于认识不足，人们赋予它的值却落在一个较大的区间内，即测量不确定度较大。

3）误差是一个理想概念，一般不能准确知道，难以定量确定；测量不确定度是反映人们对测量认识不足的程度，可以定量评定。

4）误差按自身特征和性质可分为系统误差、随机误差和粗大误差，各类误差之间并不存在绝对界限；测量不确定度不按性质分类，而是按评定方法分为A类评定和B类评定。

5）同一被测量的两个测量结果相同时，误差可相同，但是测量不确定度不一定相同；同样，当两个测量结果不同时，误差不同，但是测量不确定度可能相同。

6）误差大小取决于测量结果；测量不确定度取决于所采用的测量原理、方法、仪器、参考标准、测量条件和人员等，而与测量结果无关。

7）误差可能是正值也可能是负值，不可能同时为正负；不确定度是一个分散区间。

8）测量结果的误差已知时，即可以修正从而减小误差；不确定度已知时，不能对测量结果进行任何修正，因为它只是说明了测量结果的可疑程度。

1.5 测量不确定度在符合性判断中的应用

测量不确定度应用于诸多领域，以其在符合性判断中的应用为例，当数值处于规定的上、下限附近并要求作出符合性判断时，通过对不确定度的评定不仅可以定量地表示测量水平的高低，而且可以降低误判的风险。图2示意了测量不确定度在符合性判断中的应用，表1列出了测量结果合格与否的可能情况。

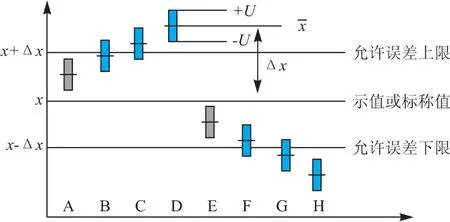
图2 测量不确定度的应用

实验室间数据的比对结果通常用比对判据En值（归一化偏差）进行评价，当En值小于或等于1时比对实验室结果符合要求，当En值大于1时比对实验室结果不符合要求，离群。用下面公式计算：

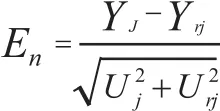
式中：En— 第j个实验室在某个测量点的En值；

Yrj— 第j个实验室在某个测量点的参考值；

Yj— 第j个实验室申报的在某个测量点的测量结果；

Urj— 第j个实验室在某个测量点的参考值的扩展不确定度；

Uj— 第j个实验室申报的在某个测量点的测量结果的扩展不确定度。

2 实验室认可中的不确定度分析

以温度二次仪表检定装置测量不确定度评定为例进行说明。

2.1 测量方法

依据JJG74—2005《工业过程测量记录仪》检定规程、JJG617 —1996《数字温度指示调节仪》检定规程、JJG951—2000《模拟式温度指示调节仪》检定规程，本装置选用多功能校验仪与被测温度仪表对同一符合规定要求的直流电位信号进行测量，分别读取多功能温度校验仪与被检定仪表的示值差，从而得到被检定仪表的示值误差。

表1 测量结果的可能情况

2.2 数学模型

ΔE=E1-E2

式中：ΔE— 被检定仪表示值误差(mV)；

E1— 被检定点的标称电势值(mV)；

E2— 与被检定点对应的实际电势值(mV)。

2.3 方差与传播系数

由于是对测量标准的不确定度进行评定，即排除被检定仪表对评定结果的影响，所以认为被测量为一相对稳定的量值，将E1假定为一常数。

依据方差定律得：uc2(ΔE)=u2(E2)，对E2的附加影响量包括：信号源的示值误差、信号源的稳定性、测量重复性、多功能温度校验仪的调节细度不够等影响。

2.4 计算分量不确定度

2.4.1 多功能温度校验仪允许误差极限所引入的不确定度分量u1

依据多功能温度校验仪说明书 ΔE=0.02%Rdg计算ΔEmax=u1= 0.16℃＝0.006 56 mV ＝6.56 μV。

2.4.2 多功能温度校验仪稳定性所引入的不确定度分量u2

本装置采用多功能温度校验仪，由说明书及检定情况得知，其电压稳定性很高，其对标准不确定度影响很小，因此u2=0。

2.4.3 多功能温度校验仪调节细度不够所引入的不确定度分量u3

由说明书得知多功能温度校验仪的调节细度为10 μV，由其产生的误差最大不超过±5 μV，估计符合等概率分布，则

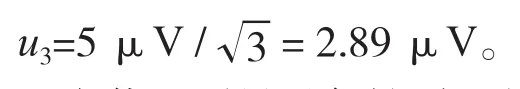
2.4.4 由装置测量重复性引入的不确定度分量u4

选择一支分度号为K 0.2级数字显示仪表编号20的作为被检仪表，在800℃检定点进行检定，在装置正常工作的条件下，用本系统进行重复测量10次，测量结果如表2。

2.4.5 标准不确定度分量（见表3）

表2 测量结果

2.5 合成不确定度

u=μV相当于 0.17 ℃

2.6 有效自由度

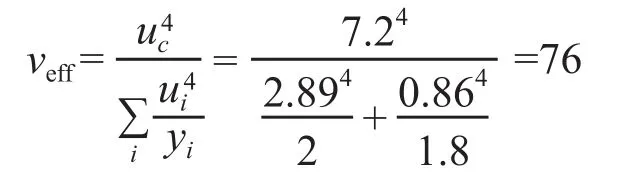
2.7 扩展合成不确定度

根据计算而得的有效自由度，veff= 76，符合正态分布，取置信概率为P=0.95时，查t分布包含因子

t0.95(76)=1.984，U0.95=1.984+7.2μV=14.30μV 相当于0.35℃，即U95=0.35℃veff=76

3 结语

示值误差和测量不确定度物理定义有本质区别，正确区分两者含义才能使不确定度在实验室认可中得以正确应用。不确定度评定是解决检测校准方法和量值溯源是否符合ISO/IEC17025标准技术要求的关键。