高亚音速大折转角叶型内激波结构与损失分析

侯宪科，姜 斌

(1.通用电气-哈动力-南汽轮能源服务(秦皇岛)有限公司，河北 秦皇岛066206;2.哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨150001)

随着现代压气机气动负荷的不断提高，针对高负荷压气机的叶型设计技术研究引起了相当的重视［1-6］，具有更高的叶栅进口马赫数(超过0.83)和更大叶型折转角的叶型研究在实验室也有所开展。文献［7-8］中，采用不同优化方法针对具有48.4°气流折转角，进口马赫数达到0.87的压气机叶栅进行了优化设计研究，叶栅试验结果表明，在超临界马赫数工况下，其性能都要优于CDA叶型。Gardner Denver公司的宋波等人［9-11］，对上述叶型进行了详细的实验测量，对优化后叶型的流场结构和损失机理进行了系统的研究。

本文从正问题分析的角度出发，采用组合多项式的方式构造了具有大折转角的高负荷压气机静叶叶型，研究了在高亚音速进口条件下，扩压叶栅内的激波结构与流动损失，探索了进一步提高压气机负荷时高亚音速大折转角叶栅内的流动特点，为进一步提高压气机负荷提供技术依据。

1 数值方法与程序校核

本文压气机叶型的造型方式选择了四次多项式为中弧线并结合双三次曲线构造厚度分布的形式。为了研究叶型参数对气动流场的影响，本文选择了叶型折转角、最大厚度、最大厚度位置、中弧线进口曲率、攻角和背压作为研究变量，进行了二维的数值模拟计算，表1给出了叶型计算方案。限于篇幅限，本文只对部分典型结果进行了分析。

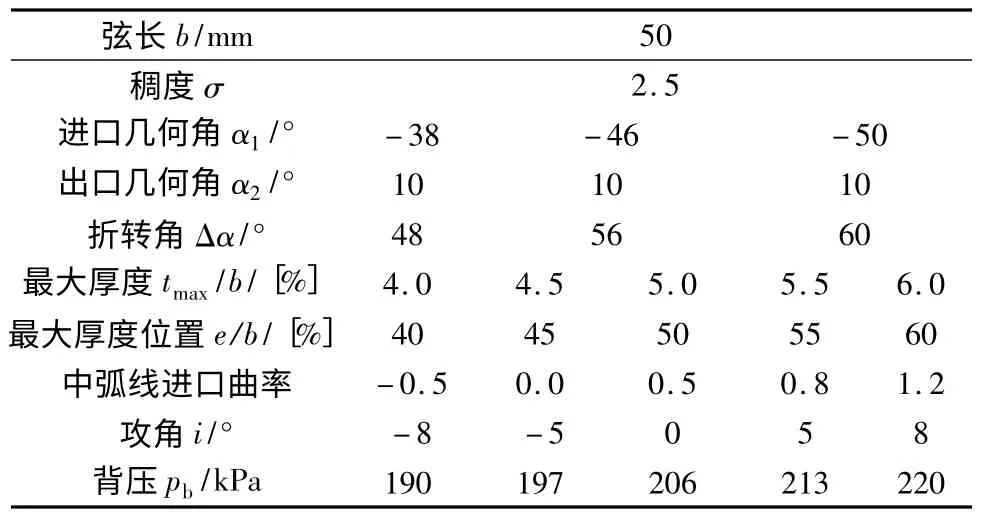
表1 叶型计算方案

流场计算采用了FINE/TURBO的Euranus二维雷诺平均N-S方程求解器。空间离散采用了二阶迎风差分格式辅以矢量分裂算法。四阶Runge-Kutta法迭代求解，多重网格加速收敛，湍流模型采用S-A模型，壁面附近平均y+﹤5。空间网格划分使用了IGG结构化网格生成模块，采用H-O-H型网格拓扑结构，网格总数26 000左右。进口边界条件，使用一致的总压249 kPa，总温387 K。在一定的攻角下，进口马赫数的变化通过调整叶栅出口背压来实现。图1给出了计算网格示意图。

图1 计算网格

本文进行程序校核的叶栅具有典型跨音速风扇顶部截面的流动特点，气流折转角3°，静压比2.15，流道内存在明显的前缘斜激波和槽道激波结构，激波前马赫数1.42～1.52。该实验是在KÖln-Porz的德国宇航研究院(DLR)的超音速风洞进行的［12］，图2给出了叶栅的几何参数。

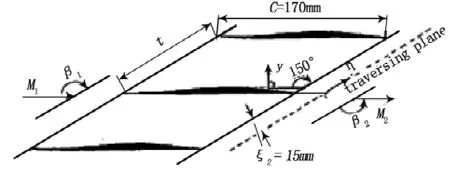
图2 跨音速叶栅几何参数［12］

图3，图4给出了采用不同的计算网格和湍流模型计算得到的叶片表面等熵马赫数的分布情况。在网格方面，其中Coarse mesh，Normal mesh，Finemesh分别代表20 000，60 000，180 000网格总数。从中可以看出，不同网格的计算结果与实验结果符合的比较好，对激波位置和吸力面上激波前预压缩段的预测存在一定的不足。在湍流模型方面，单方程模型和两种Kepsilon模型预测的吸力面上激波位置更偏向下游，也与实验位置更接近，所有的模型预测的吸力面激波前等熵马赫数都偏高。而对于压力面前段激波情况的预测，只有一方程S-A模型与双方程的Kepsilon of Yang模型预测的结果与实验结果接近。

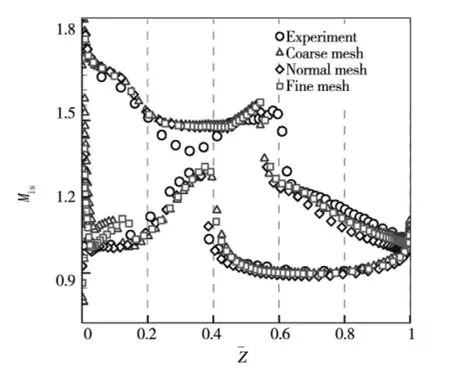
图3 网格的影响

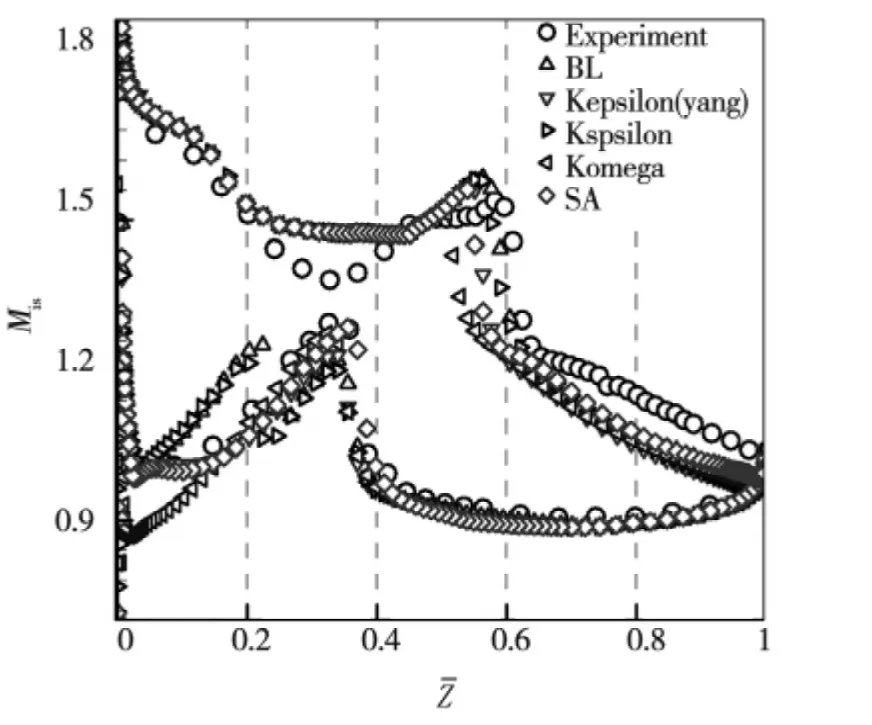
图4 湍流模型的影响

综上，可见本文采用的算法能够对跨音速压气机叶型内部的激波结构进行较好的描述，网格总数在2万左右已经可以较好的描述激波位置，S-A对激波位置和强度的描述较好，同时计算速度较快，能够保证大量的方案计算。

2 高亚音速大折转角叶栅内的激波结构

通过大量的数值模拟研究，本文给出了高亚音速大折转角压气机叶栅流道内详细的流场结构，并重点讨论了流场当中可能存在的各种激波结构［12-16］。图5给出了中弧线进口曲率为0.0，最大厚度位置在50%相对轴向位置，背压为197 kPa，不同攻角时叶栅内的马赫数的云图。以此为例，可见在高亚音速的进口条件下，大折转角叶型由于吸力面折转造成了流道内处于马赫数较高的情况，存在明显的激波结构。由图中可见，按照前面所给出的边界条件，随着攻角的增加，进口马赫数不断提高，叶栅内的流场结构发生了显著的变化。在负攻角时，流道内发生流动阻塞，流场中存在典型的槽道激波结构，气流经过叶片吸力面前半部分的加速，以及由于负攻角在叶片的前半弦长形成了实际的收缩流道，在叶片吸力面50%弦长左右位置，高速气流终止于吸力面上的一道正激波。这种在吸力面上形成局部的超音速区域，并终止于一道正激波的结构是高亚音速进口条件下大折转角流动的普遍特点。随着攻角的增加，流场结构发生一定的变化，在+5°攻角的情况下，由于来流马赫数的增加和前缘的绕流，在叶片的前缘吸力面侧形成了另外一个范围较小的超音速区域，与槽道内的超音速区域类似，终止于一道正激波。随着攻角的进一步增加，在+8°攻角的情况下，前缘附近的超音速区域发展成为前缘的斜激波，并与槽道的正激波形成类似跨音速压气机动叶顶部设计点的激波结构。从图中可见，8°正攻角时叶型的进口马赫数较高，达到1.1，虽然形成了较强的激波结构，但是激波后的附面层没有发生大的分离现象。

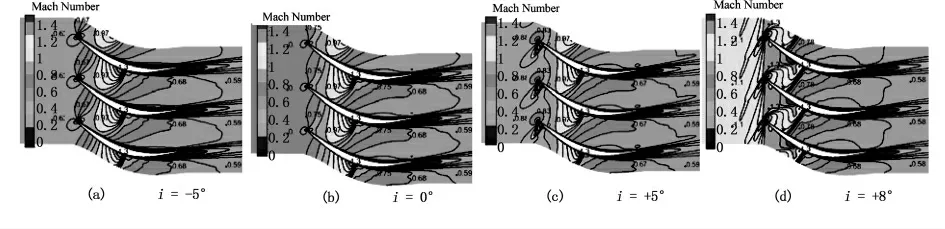
图5 不同攻角情况下马赫数等值线(KK1=0.0，e/b=0.5，Pb=197 kPa)

经过对不同工况的总结，可以得到高亚音速大折转角压气机叶型可能存在典型激波结构:首先对应流道处于堵塞状态，此时进口马赫数不算很高，一般叶型工作在负攻角的状态下，由于吸力面上的绕流在流道中间位置形成局部的超音速区域，并终止于一道正激波，随着背压和攻角的增加，这道槽道激波会向上游移动。其次，在背压较低，叶型转角不太大，正攻角也较小的时候，流道内会演化成另外一种激波结构，此时，流道内的槽道正激波还没有到达叶片前缘，由于正攻角的作用在叶片前缘吸力面又出现另外一个较弱的超音速区域和一道正激波，这是一个过渡状态，这个超音速区域的发展最终演变成为前缘激波。随着正攻角与来流马赫数的进一步提高，流道内的激波结构变为一种类似于跨音速动叶顶部在设计点时的激波结构。

3 高亚音速大折转角叶栅内的损失分析

为了给出高亚音速进口条件下，具有大折转角特点的压气机叶栅损失分布特点。文中针对具有48°几何折转角的叶型，在不同攻角和出口背压情况下的损失进行了分析。图6给出了叶型出口熵沿周向的分布，详细的分析了高亚音速进口条件下，流道内损失的分布情况。

图6中纵坐标为熵的大小，横坐标为圆周方向的相对位置，坐标0代表尾缘处，吸力面侧为大于0的一侧，压力面一侧坐标小于0。从图6中能够看到，在背压为197 kPa的情况下，流道内流动处于进口马赫数较高的工况下，激波强度也较强一些。图中熵值很高的区域对应出口的尾迹区域，其能够描述尾迹的宽度和尾迹损失的大小。从图中来看，吸力面一侧的尾迹随着攻角的增加，有所增加，熵值也较大，压力面侧的尾迹虽然宽度较小，但是由于攻角不同引起的改变较大，在负攻角的情况下，压力面侧尾迹的宽度和损失的大小都会迅速的增加。可见此类叶型对于负攻角十分的敏感也是流动容易恶化的工况。势流区域的损失受攻角的影响变化较小，这部分损失与激波损失相关，只是在+8°攻角的情况下，势流区域的损失具有较大的提高，此时，进口的马赫数较高，流道内是前缘激波与槽道激波共存的激波结构，激波损失较大。另外一个值得注意的是，在尾迹区域靠近吸力面一侧，尾迹损失的大小沿圆周方向基本不变，这一点与不存在激波结构时的图6(b)是不同的，可以推断，此时叶栅吸力面上的附面层受到激波作用的影响形成了一段在圆周方向损失分布比较均匀的区域，原有的附面层内的损失分布规律被打乱，这段区域损失的大小不仅受攻角的影响，同时受激波位置和强度的影响明显。

图6 尾缘处熵沿周向的分布(KK1=0.0，e/b=0.5)

在背压增加到213 kPa后，流道内的流动处于进口马赫数相对较低的情况，此时，流道内不存在明显的激波结构，势流区内的损失受攻角的影响很小，而且在圆周方向基本不发生变化，但是尾迹区域内的损失受攻角的影响十分明显，特别是在吸力面一侧。与存在一定激波结构的197 kPa背压情况不同，此时，攻角的增加，十分明显的增加了尾迹的宽度以及损失的大小，正攻角时的叶型损失远大于没有攻角的情况。

从上面对两种背压情况下损失的分析能够看到，在流道内存在明显的激波结构时(197 kPa)，尾迹宽度受攻角的影响较小，来流方向的改变只是改变了流道内的激波结构，由于激波的存在，使尾迹宽度对攻角的敏感性下降，在大攻角情况下激波强度会有所增加，激波损失相应的增大。而当流道内是亚音速流动时(213 kPa)，势流区损失基本不会发生变化，随着攻角的增加，吸力面叶型损失迅速增加，负攻角时压力面侧损失较大。

结合前一部分讨论的激波结构可以发现，按照激波处于流道内的不同位置，激波与附面层相互作用对叶型损失的影响大致可以分为两种情况，其一在负攻角或零攻角时，激波处于槽道内，此时，随着攻角的增加，槽道激波向喉部移动，此时激波附面层相互作用产生的叶型损失则会有所增加;另外，随着前缘激波的形成以及单激波结构溢出流道，激波位置远离叶栅喉部会减小相应的叶型损失。也就是说，激波与吸力面的交点处于吸力面最低压力点附近时，其对叶型损失的影响最为严重，在很大程度上增加了叶型损失。

4 结论

本文通过对高音速大折转角压气机叶型进行数值模拟，研究了流场内的激波结构和损失分布情况，针对高亚音速大折转角压气机叶型可以得到如下结论:

(1)在不同的攻角和马赫数情况下，叶栅内存在着不同的激波结构。在负攻角时，在叶型的吸力面中间位置形成局部超音速区域，并终止于一道槽道正激波，造成流道阻塞。在较小的正攻角时，流道内的槽道正激波还没有到达叶片前缘，在叶片前缘吸力面又出现另外一个较弱的超音速区域和一道正激波，这是一个过渡状态。随着正攻角与来流马赫数的进一步提高，流道内的激波结构变为一种类似于跨音速动叶顶部在设计点时的激波结构。

(2)对于大折转角静叶栅，流道内的激波位置与强度对叶型损失的大小影响显著，计算结果表明，激波与附面层相互作用改变了原有的附面层内的损失分布规律，形成了基本由激波强度和位置所决定的沿叶片表面法线方向大小不变的高损失区域。叶型损失的大小和激波与吸力面最低压力点之间的相对位置密切相关。

［1］赵鹏程，刘波，宣扬，等.基于遗传算法的压气机叶型优化设计［J］.航空计算技术，2011，41(6):12-15.

Zhao Pengcheng，Liu Bo，Xuan Yan，et al.Optimization for Compressor Airfoil Based on Genetic Algorithm［J］.Aeronautical Computing Technique，2011，41(6):12-15.

［2］王娥，杜鑫，温风波，王松涛.地面重型燃气轮机压气机叶型的优化设计［J］.汽轮机技术，2010，52(1):9-12.

Wang E，Du Xin，Wen Fengbo，Wang Songtao.Optimization Design on Ground-based Heavy-duty Gas Turbine Compressor Blades［J］.Turbine Technology，2010，52(1):9-12.

［3］Benini E.，Toffolo，A Development of High-Performance Airfoils for Axial Flow Compressors Using Evolutionary Computation［J］.Journal of Propulsion and Power，2002，18(3):544-554.

［4］Oksuz O.，Akmandor I.，Kavsaoglu M..Aerodynamic Optimization of Turbomachinery Cascades Using Euler/Boundary-Layer Coupled Genetic Algorithms［J］.Journal of Propulsion and Power，2002，18(3):652-657.

［5］Rai M.，Madavan N.Application of Artificial Neural Networks to Design of Turbomachinery Airfoils［J］.Journal of Propulsion and Power，2001，17(1):176-183.

［6］Yiu K.F.C.，Zangeneh M.Three-Dimensional Automatic Optimization Method for Turbomachinery Blade Design［J］.Journal of Propulsion and Power，2000，16(6):1174-1181.

［7］Yamaguchi Y.，Arima T.Multi-Objective Optimization for the Transonic Compressor Stator Blade［C］.AIAA Paper，2000-4909，Atlanta，Georgia，2000.

［8］Olhofer M.，Arima T.，Sonoda T.，Sendhoff B.Optimization of a Stator Blade used in a Transonic Compressor Cascade with Evolution Strategies.Adaptive Computation in Design and Manufacture［M］.edited by I.Parmee，Springer-Verlag，Berlin/New York/Heidelberg，2000.

［9］Song B，Ng W.Influence of Axial Velocity Density Ratio in Cascade Testing of Supercritical Compressor Blades［C］.AIAA Paper，2004-3414，Reno，Nevada，2004.

［10］Song B.，Ng W.Performance and Flow Characteristics of an Optimized Supercritical Compressor Stator Cascade［J］.Journal of Turbomachinery，2006，Vol.128，July，pp.435-443.

［11］Song B.，Ng W.Loss Mechanisms of High-Turning Supercritical Compressor Cascades［J］.Journal of Propulsion and Power，2008，24(3):416-423.

［12］Schreiber H.A.，Starken，H.An investigation of a Strong Shock-Wave Turbulent Boundary Layer Interaction in a Supersonic Compressor Cascade［J］.Journal of Turbomachinery，1992，Vol.114，pp:494-503.

［13］孙晓东，韩万金.压气机叶片多二次气动优化设计研究［J］.汽轮机技术，2010，52(1):24-26.

［14］李毅刚，王会社，钟兢军，等.双圆弧叶型压气机叶栅气动特性的实验研究［J］.2002，44(2):91-94.

［15］丁怀臣，赵俊明，黄钢.多纹轴流压气机皮通模拟与改进设计［J］.汽轮机技术，2007，49(1):14-16.

［16］王祥锋，周逊，王松涛，等.动叶正弯对压气机性能影响的数值研究［J］.汽轮机技术，2009，51(6):401-403.