基于结构模式的道路网节点匹配方法

栾学晨，杨必胜，李秋萍

1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；2.武汉大学时空数据智能获取技术与应用教育部工程研究中心，湖北 武汉 430079；3.广东瑞图万方科技股份有限公司，广东 佛山 528305；4.中山大学 地理科学与规划学院，广东 广州 510275

1 引 言

随着地理空间数据获取与处理技术的快速发展，数据的融合、集成与增量更新成为地理空间数据库建设的一个重要方面。但多源道路网数据中常存在格式结构多样、缺乏统一生产规范等问题，需要建立有效的多源道路网数据匹配方法，例如缓 冲 区 方 法［1－4］、计 算 道 路 之 间 的 几 何 距 离（Euclidean、Hausdorff、Fréchet距离等）［5－7］和 结构拓扑方法［8－9］。在得到道路候选匹配指标的基础上，可以进一步使用概率和迭代的方法寻找道路网数据最优化匹配，剔除错误匹配，确定最终的匹配结果［10－13］。但是上述方法要求道路网数据之间的定位精度近似一致。然而由于制图误差、数据尺度差异、坐标系统不同以及位置加密等因素的影响，当多源道路网数据参考系存在差异时，利用几何位置作为匹配参考非常困难。

数据精度和空间参考一致性问题是地理信息系统的基本问题之一，通常需要人工寻找同名点进行校正［14］。但是人工校正工作量大、自动化程度低。为实现不同参考系数据的自动匹配，文献［15］提出了一种根据相似节点构建坐标系转换方程的方法，通过计算节点的道路连接数、道路夹角，以及节点连接方向、距离等指标来寻找不同数据中的相似节点。但是该方法描述的节点特征过于简单，使数据间存在大量相似节点，导致算法的计算代价较高。而且该算法未考虑坐标系之间旋转变形，要求数据之间的长度单位须保持一致，且不支持多尺度表达数据之间的匹配，使得应用该方法受到相当的限制。

针对以上问题，本文提出一种基于道路结构模式的匹配方法，使用局部网络结构来描述道路的形态特征与拓扑关系，并通过比较待匹配道路间的结构相似性，确定最优的道路匹配。本方法不依赖道路网的定位精度，尤其适用于多源数据的坐标系统不一致的情况。

2 道路网数据预处理

数据结构的一致性是匹配的基础，目前大多数道路网数据都采用点线结构的几何存储［1－14］，对于少数多边形结构的道路数据可采用骨架线、中心点提取方法转化成点线结构后再进行匹配处理［16－17］。本文重点研究针对点线结构的道路网节点匹配。

由于尺度和应用目的的不同，多源道路网数据在表达方式和拓扑结构上可能存在差异。因此数据预处理主要包括复杂道路和交叉口结构的提取与拓扑关系重建两步。

首先，多源道路网数据中的同一条道路与交叉口可能有多种存储形式，如图1所示：道路可能存储为多线车道，或者单一条道路中心线；另外道路交叉口也可能存储为环岛、立交桥形式，或者单一节点。本文使用文献［18］中的方法，通过平行线探测和聚类分析识别道路网中的多线车道与复杂交叉口模式。在此基础上将道路网中属于同一条复杂道路与交叉口的道路弧段与节点赋值为相同的ID，并以此修正拓扑连通关系。在此基础上计算提取后的道路长度与方向，分别为道路合并后起止点之间的最短路径与连线方向。

其次，多源道路网数据在拓扑结构上也可能不同。如图2所示，图（a）道路多段线只在允许转向的交叉口处打断（如导航地图数据），或者图（b）道路多段线在交叉口处一律打断（如基础地理数据）。由于结构图（b）实际上是在结构图（a）基础上添加全部交叉点所得。因此本文将所有待匹配的道路网数据统一为结构图（b），即两条道路的相交处一定被认为是交叉口。同时通过剔除连接数等于2的伪节点（图2（c）），保证凡道路节点必出现在交叉口处。

图1 道路和交叉口的多种表达形式Fig.1 Multi－representation of roads and junctions

图2 道路网存储结构Fig.2 Storage structure of road network

3 道路节点结构相似性计算方法

3.1 道路交叉口的局部网络结构描述

本文通过记录与每个道路交叉口连接的道路网所构成的局部网络结构来描述道路节点的形态和拓扑信息。如图3所示，局部网络中的所有节点和弧段的坐标与连通关系都被记录。其中被描述的交叉口定义为中心节点，与中心节点直接相连的道路定义为主边，并记录主边之间的逆时针邻接关系。主边与其他邻接道路共同构成局部网络。理论上当邻近道路数足够多时，每个道路交叉口都具有唯一的结构特征使其能够相互区分，该局部结构便是中心节点的唯一结构化特征描述。实际匹配中采用三阶连通道路能够描述一个道路节点的结构特征。

3.2 局部网络结构配准

根据道路节点的局部网络结构描述，可以将道路中的节点距离匹配转化为局部网络之间的形态相似性匹配。每个道路交叉口生成的局部网络总能在另一份数据中找到最优匹配。由于多源数据参考系的不同，需要首先配准两个局部网络使其具有可比性。本文使用局部网络中的街区作为配准参考。配准过程如图4所示，假设局部网络LN1与LN2分别包含两个街区，任意两个街区之间都可以构建一个仿射变换，例如如果根据A1－B2进行变换，由于记录了主边的逆时针邻接关系，可以得到3对变换控制点o1－o2、c1－b2和a1－c2并构建仿射变换。

图3 道路交叉口局部网络描述示意图Fig.3 Example of local network description

图4 街区配准示意图Fig.4 Examples of blocks registration

对于图4所示的情况，LN1与LN2共有4种可能的变换。但其中A1－A2与B1－B2的街区之间可能会得到相似的变换方程。本文通过长度比值计算合并相似变换，提高计算效率。如果局部网络中的两个街区共享一条主边并且位于共享边两侧，则将其合并为一组。易证明处于同一条直线上的线段在仿射变换前后的长度比值保持不变。如图4中的粗线所示，如果a1o1与o1b1共线，且在仿射变换后的线段分别为a2o2与o2b2，则应有

反之，如果两个局部网络中存在相等的长度比值，则对应的街区归组应具有相同的变换方程。即如果先有公式（1）成立，则可以根据4对变换控制点o1－o2、a1－a2、b1－b2和c1－c2构建一次仿射变换。

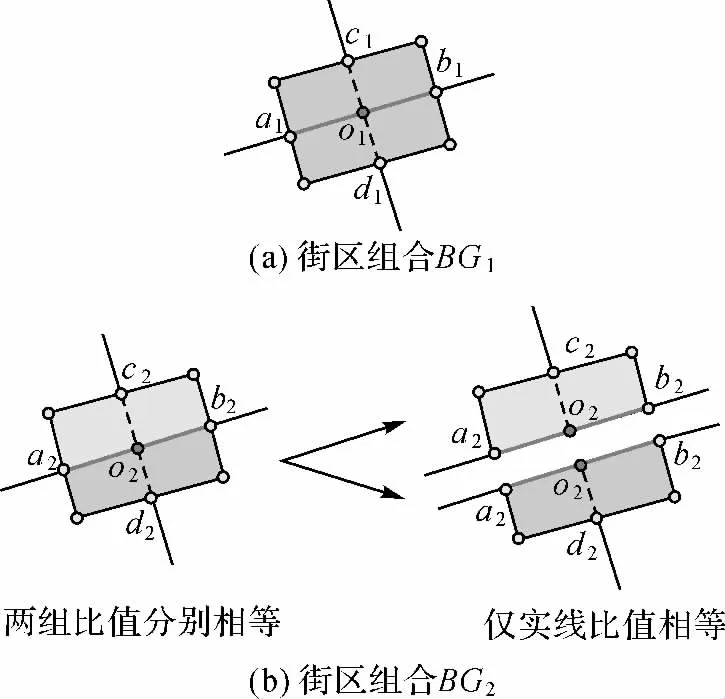
图5 街区组合匹配示意图Fig.5 Examples of block groups matching

3.3 最大公共子网查找

通过建立变换方程，将两个局部网络变换到同一参考系下，使之具有可比性。由于局部网络之间可能存在多个变换，对于每一种变换，都可以得出一个相似度。局部网络之间的相似度可以通过计算最大公共子网（maximum common subnetwork，MCS）获得，即寻找两个网络的最大公共部分。本文采用树形查找的方式进行［19］。首先以两个局部网络中的中心节点作为查找的起点，比较连接道路的相似性。比较方法如图6所示，O1与O2为两个局部网络的中心节点，Road1和Road2为两条连接路段。算法平移O1至O2并判断Road’2和Road1的夹角Angle12：如果小于阈值，则认为二者为公共路段。用Road’2与Road1的较短路段长度截断另一条路段，并以截点O3与O4为新的起点继续查找后续的连通路段；如果夹角Angle12大于阈值，则退回起点O1与O2。算法采用广度优先搜索查找其他连接路段直至遍历所有道路，所有找到的公共路段组成局部网络的最大公共子图。

图6 道路相似性比较Fig.6 Similarity comparison of roads

最大公共子网的查找揭示了特定变换方程下局部网络之间相似部分的范围，在此基础上进行结构相似性的计算，量化这种相似度的大小。本文提出道路网编辑距离（road network edit distance，RED）指标计算道路交叉口之间的结构相似性。RED定义为给定两个局部网络，通过对其中一个网络进行修改，可以得到另一个网络，修改操作可以分为添加、删除和替换操作［20］，此处的3种操作并非真正对道路网进行修改，只是一种分类。其中每种操作的代价不同，一般规定替换操作比添加与删除操作具有更小的修改代价。两个局部网络之间可能的修改方式有多种，修改代价存在极值。其中代价最大修改方式是将一个局部网络中的所有路段删除，然后添加另一个网络中的所有路段；而特定变换方程下的最小修改代价即为RED，数学表述如公式（2）所示。

式中

对于两个局部网络中的任意一种变换trans都存在一个相关的RED值，本文综合得到的所有RED的最小值MiRED作为局部网络的最终相似性指标。

MiRED反映了在允许进行拉伸、平移、切变等变换的情况下等价两个局部网络所需的最小代价，体现了两个局部网络所等达到的最大重叠率，可以用于坐标系与尺度未知的情况下衡量两个道路交叉口的结构相似性。

4 基于空间位置的匹配修正

道路交叉口结构相似性指标MiRED可以对大多数道路交叉口寻找最佳匹配。但在两份数据间详细程度差异较大的区域，许多交叉口实际上没有对应的匹配，还有部分节点由于形态特征差异较大而产生匹配错误。需要进一步设计匹配优化算法，提高匹配效果。

一般认为，如果两份道路网数据能够进行匹配，则数据间的整体形态结构应当相似，大部分道路交叉口应当能够匹配；而错误匹配从几何偏差上看位置错误明显，属于明显的粗差。因此为了实现道路网的最佳匹配，本文首先采用稳健的M估计方法，根据形态匹配的道路节点对两份道路网进行空间配准，然后根据配准后道路网道路节点的几何距离提出粗差，结合形态相似性MiRED的计算结果共同确定最终的道路交叉口匹配。如果存在多个道路交叉口对应同一交叉口，则该匹配为1∶n匹配；如果反之亦成立，则为m∶n匹配；如果形态匹配的所有结果都超出了校正后的距离阈值，则该形态匹配为1∶0匹配。本文使用仿射变换配准两份道路网数据，如公式（4）所示

仿射变换具有6个独立变量，需要最少3对不共线的同名控制点。当控制点多于3对时，使用M估计进行平差。根据M估计，该仿射变换的参数计算可转换为公式（5）的最小二乘问题

下标i表示第i对匹配节点之间的距离，上标k表示迭代数。权重函数ω（x）反映该匹配节点对于变换方程参数估计的影响值。在稳健估计中，应当保持可靠匹配的权重，降低不可靠匹配的权重，可使用IGG3权重函数进行迭代计算［21］

当残差r小于阈值a时，权值函数保持不变；当r在a到b的区间内逐渐增加时，权值函数呈下降曲线；当残差r的大于阈值b时，则认为该匹配错误，权值为0。每次迭代都将计算新的权值。

除了消除错误匹配，稳健估计过程对于道路网的结构匹配过程还有以下作用：

（1）初始的节点匹配需要遍历比较任意两个道路交叉口之间的结构相似性，而稳健估计之后能够初步配准两个道路网数据，使得后续的匹配过程可以在每个交叉口的缓冲区范围内查找，能够明显地减少搜索范围；

（2）由于稳健估计能够得到两份道路网数据坐标系之间的近似变换方程，记为transapprox.。因此，由公式（3）计算的MiRED可以近似地使用transapprox.变换下的RED值代替，如公式（7）所示

该式能够显著降低MiRED的计算时间，而且对于不存在街区结构的局部网络也能够计算其结构相似性。

5 试验结果分析

本文选取了武汉市1994年基础地理数据（数据1）与2006年导航地图数据（数据2）进行匹配试验。两份数据时间跨度超过10年，许多区域的几何和语义信息发生变化，具有较好的匹配意义。数据1有731个道路交叉口，数据2有361个道路交叉口。由于数据加密的影响，数据间无统一的坐标系统，无法使用几何匹配。因此本文的匹配使用基于结构相似性的比较方法。试验最终匹配数据1节点416个，匹配率为57%，反映了两份数据之间存在较大的几何变化。

图7所示的是数据1中一个节点的局部网络与数据2中多个节点的MiRED比较结果，两份数据的道路分别表示为黑色与灰色。取其中MiRED最小的3组匹配，需要替换操作的道路用深色线表示，即两个局部网络的公共部分。可以看出图7（a）中正确的节点匹配具有最小的MiRED值，较之于其余两种比较结果，区分效果较好。

图7 节点的MiRED比较Fig.7 MiRED comparison of nodes

但是MiRED对道路网不同区域中结构形态相似的区域也可能产生匹配错误。例如由于实际路网的变化，使得图8所示的数据1中的中心节点在数据2中不存在对应节点，即1∶0匹配。而通过MiRED计算会强行寻找一个满足阈值的相似程度最高的交叉口，导致错误匹配。

图8 错误的MiRED匹配Fig.8 False MiRED matching

图9显示了对两份数据配准后的MiRED匹配点之间距离偏差的计算结果。由统计图可以看出，形态相似性匹配能够对大多数节点进行匹配，符合稳健估计的应用条件，并且能够通过坐标系配准后的距离偏差剔除错误匹配。

图9 坐标系配准后匹配交叉口距离统计图Fig.9 Distance statistics of node matching after registration

最后，使用位置偏移值修正形态匹配结果，得到最终的道路匹配，局部结果如图10所示。包含在同一个椭圆内的点对表示道路交叉口的匹配关系。对全部731对交叉口匹配结果进行统计，结果如表1所示，其中共正确匹配交叉口（1∶n匹配算作n对匹配点）329对，正确率为97%，错误匹配率仅为3%，说明本文提出的结构相似性指标具有很好的形态区分性。但是算法遗漏匹配率高达20%。这是由于两份匹配数据在部分地区的道路变化较为明显，使得同一道路交叉口的局部网络形态差异过大而无法匹配。这一问题可以通过缓冲区距离方法得以弥补。对于试验中未能正确匹配的77个交叉口进行缓冲区匹配，其中73个交叉口能够找到正确的对应节点。可以看出，使用形态相似性的方法能够在数据位置偏移较大的情况下识别出绝大部分的匹配交叉口，且匹配结果较好。

表1 匹配结果统计Tab.1 Statistical results of matching

图10 局部匹配结果图Fig.10 Matching result in local area

6 结 论

多源道路网数据级联更新的关键技术之一是道路匹配，其目的是确定多份数据中对应的同名道路要素，匹配效果不佳或出现错误匹配直接影响更新结果的正确性。本文提出的基于道路交叉口结构相似性确定道路匹配方法符合人工匹配道路的过程，匹配结果可靠；依据三阶连通的局部网络模式描述有效地表达了每个道路交叉口的形态信息，且对于数据的空间位置不具有依赖性，在数据定位精度差异较大的情况下仍能够达到较好的匹配效果，提高了算法的适应能力。试验结果表明本文方法很好地解决了不同定位精度下同名道路的匹配问题，而且匹配结果与人工判断结果相似，弥补了传统方法对于道路坐标系必须保持一致性的限制。在匹配基础上不仅可以对未匹配的道路进行变化检测，还可用于多源数据综合分析、数据拼接、建立多尺度数据库关联等多个方面。但是本文方法重点在于道路节点的结构匹配，在同语义信息、几何位置信息的综合，以及根据已匹配的节点进行道路路段的匹配研究方面尚存在不足。另外，对于如何在匹配基础上实现更新操作问题，涉及坐标变换内插与拓扑关系保持，以及几何、语义、元数据一致性等，也是后续工作的研究重点。

［1］ HU Y G，CHEN J，ZHAO R L，et al.Matching of Roads under Different Scales for Updating Map Data ［J］.Geomatics and Information Science of Wuhan University，2010，35（4）：451－456.（胡云岗，陈军，赵仁亮等.地图数据缩编更新中道路数据匹配方法［J］.武汉大学学报：信息科学版，2010，35（4）：451－456.）

［2］ WALTER V，FRITSCH D.Matching Spatial Data Sets：a Statistical Approach ［J］.International Journal of Geographical Information Science，1999，13（5）：445－473.

［3］ ZHANG M，SHI W Z，MENG L Q.A Generic Matching Algorithm for Line Networks of Different Resolutions［C］∥Workshop of ICA Commission on Generalization and Multiple Representation.Coruña：［s.n.］，2005.

［4］ ZHANG M，MENG L Q.Delimited Stroke Oriented Algorithm－Working Principle and Implementation for the Matching of Road Networks［J］.Annals of GIS，2008，14（1）：44－53.

［5］ MUSTIÈRE S，DEVOGELE T.Matching Networks with Different Levels of Detail ［J］.GeoInformatica，2008，12：435－453.

［6］ CHEN Y M，GONG J Y，SHI W Z.A Distance－based Matching Algorithm for Multi－scale Road Networks［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：84－90.（陈玉敏，龚健雅，史文中.多尺度道路网的距离匹配算法研究［J］.测绘学报，2007，36（1）：84－90.）

［7］ ZHANG M，MENG L Q.An Iterative Road－matching Approach for the Integration of Postal Data［J］.Computers，Environment and Urban Systems，2007，31（5）：598－616.

［8］ YING S，LI L，LIU W Z，et al.Change－only Updating Based on Object Matching in Version Databases ［J］.Geomatics and Information Science of Wuhan University，2009，34（6）：752－755.（应申，李霖，刘万增，等.版本数据库中基于目标匹配的变化信息提取与数据更新［J］.武汉大学学报：信息科学版，2009，34（6）：752－755.）

［9］ DENG M，XU K，ZHAO B B，et al.A Hierarchical Approach for Nodes Matching Based on Structural Spatial Relations ［J］.Geomatics and Information Science of Wuhan University，2010，35（8）：913－916.（邓敏，徐凯，赵彬彬，等.基于结构化空间关系信息的节点层次匹配方法［J］.武汉大学学报：信息科学版，2010，35（8）：913－916.）

［10］ TONG X H，DENG S S，SHI W Z.A Probabilistic Theorybased Matching Method ［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：210－217.（童小华 邓愫愫，史文中.基于概率的地图实体匹配方法［J］.测绘学报，2007，36（2）：210－217.）

［11］ ZHAO D B，SHENG Y H.Research on Automatic Matching of Vector Road Networks Based on Global Optimization［J］.Acta Geodaetica et Cartographica Sinica，2010，39（4）：416－421.（赵东保，盛业华.全局寻优的矢量道路网自动匹配方法研究［J］.测绘学报，2010，39（4）：416－421.）

［12］ VOLZ S.An Iterative Approach for Matching Multiple Representations of Street Data［C］∥ISPRS Workshop Multiple Representation and Interoperability of Spatial Data.Hannover：［s.n.］，2005.

［13］ YANG B S，ZHANG Y F，LUAN X C.A Probabilistic Relaxation Approach for Matching Road Networks［J］.International Journal of Geographical Information Science.2013，27（2）：319－338.

［14］ CHANG Kangtsung.Introduction to Geographic Information System ［M］.Translated by CHEN Jianfei.Beijing：Science Press，2003.（张康聪.地理信息系统导论［M］.陈健飞，译.北京：科学出版社，2003.）

［15］ CHEN C C，SHAHABI C，KNOBLOCK C A，et al.Automatically and Efficiently Matching Road Networks with Spatial Attributes in Unknown Geometry Systems［C］∥Proceedings of the 3rd Workshop on STDBM.Seoul：［s.n.］，2006.

［16］ MUSTIÈRE S.Results of Experiments on Automated Matching of Networks at Different Scales［C］∥Proceedings of Multiple Representation and Interoperability of Spatial Data.Hannover：［s.n.］，2005.

［17］ KIELER B，HUANG W，HAUNERT J H，et al.Matching River Datasets of Different Scales［C］∥Proceedings of 12th Annual AGILE Conference on Geographic Information Science.Hannover：［s.n.］，2009.

［18］ YANG B S，LUAN X C，LI Q Q.Generating Hierarchical Strokes from Urban Street Networks Based on Spatial Pattern Recognition［J］.International Journal of Geographical Information Science.2011，25（12）：2025－2050.

［19］ XIONG D M，SPERLING J.Semi－automated Matching for Network Database Integration［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2004，59（20）：35－46.

［20］ CONTE D，FOGGIA P，SANSONE C，et al Thirty Years of Graph Matching in Pattern Recognition ［J］.International Journal of Pattern Recognition and Artificial Intelligence，2004，18（3）：265－298.

［21］ YANG Y X.The Equivalent Weight Principle－Robust Least Squares Solution Estimation of Parameters Adjustment Model［J］.Bulletin of Surveying and Mapping，1994，6：33－35（杨元喜.等价权原理—参数平差模型的抗差最小二乘解［J］.测绘通报，1994，6：33－35.）