基于LMS的自适应直放站回波消除算法研究

王 鹏 ，王明泉 ,李晓阳 ，乔佳亮

（中北大学 a.仪器科学与动态测试教育部重点实验室；b.信息与通信工程学院，山西 太原 030051）

随着手机（数字电视）用户迅猛增长，客户对覆盖网络优化的要求越来越严格，但由于受到地势、功率大小等因素的影响，一些地区的网络信号难以保持良好，如高楼的阴影区、地下停车场、边远的郊区、农村等，因此数字电视的盲区覆盖成为下一步网络建设的重点[1]。所以，解决数字电视地面网络信号覆盖盲点问题就需要使用数字转发器。

直放站收发天线耦合的回波抑制对于整个转发系统来说起着很重要的作用。同频直放站同时具有接收天线和发射天线，而且同频转发的情况下，转发器的输出为大功率的射频信号，与转发器的输入是同频的，而收发天线间的耦合作用会使部分转发的信号反馈到直放站接收端，在接收天线端产生了经过多径的回波耦合信道和延迟后的回波信号，即耦合回波信号，如果不处理，不仅会提高接收机的误码率，严重时还会导致系统自激[2]。

为了解决上述问题，美国、欧洲、日本对此做了大量工作，有的采用RLS算法，有的采用NLMS算法，但LMS算法较为简单。我国也非常重视ICS（Interference Cancel System）数字无线直放站的研发。目前较为常用的思路是，利用所采用的算法估计出回波信道，在数字基带进行抵消，即可输出期望的信号。

1 LMS算法

LMS算法自20世纪60年代初提出以后得到了广泛的应用。LMS算法最核心的思想是平方误差代替均方误差。文献[3]中作者指出LMS算法的基本关系式为

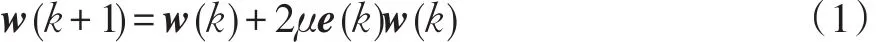
LMS算法进行梯度估计是以误差信号每一次迭代的瞬时平方值来代替均方值[4-5]，LMS的迭代权值更新算法式为

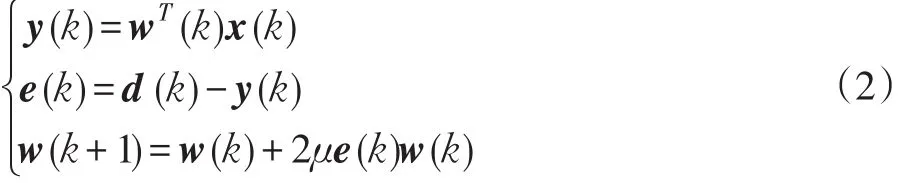
式中：w（k）为滤波器的权值系数；μ为自适应滤波器的收敛因子，控制自适应算法的速度和稳定性。为了保证算法收敛，需满足0〈μ〈λmax，其中λmax为输入信号的最大特征值。一般，超量均方误差Jex等于稳态均方误差的数学期望E[J（n）]与最小均方误差Jmin之差，即

在稳态情况下

当μ较小时，上式可表示为

由式（4）和式（5）得到LMS算法的失调为

自相关矩阵R的平均特征值为

平均时间常数τmse,av定义为

故

所以，可得失调

由此可得μ越大，自适应滤波器的收敛速度越快，但是会有较大的失调误差；相反，μ越小，收敛速度越慢，失调误差越小[6-8]。

2 基于LMS算法的回波抵消

同频直放站对输入信号接收后，经过一些列信号处理后以相同的频率将信号发射。同频直放站的难度在于由于发射链路和接收链路同频，所以发射信号会以不同的形式或多或少地耦合到接收链路上（通常将这个信号叫作回波信号），这样，在系统增益不高的情况下，会影响输出信号的质量，在系统增益较高的情况，会引起系统的自激，使系统不能稳定工作，甚至烧毁后级功放。所以在同频直放站设计中如何减小回波对整个系统的影响成为设计上的最大挑战。而回波信号本质上是系统的接收信号放大后，加噪声和延时的同频信号，针对回波信号的以上两个特点本文采用了基于LMS算法的自适应FIR滤波器，用FIR滤波器的特性模拟发射天线到接收天线的链路特征，通过FIR滤波器计算出发射到接收天线的回波并消除。原理如图1所示。

图1 算法整体框图

1）用LMS算法计算出最优的的FIR的值。首先，给系数设定一个初值作为参考信号，然后参考信号对输入信号开始作用，开始自适应调整加权系数，最终求得一个合理的e（n）y*（n-k）。原理如图2所示。

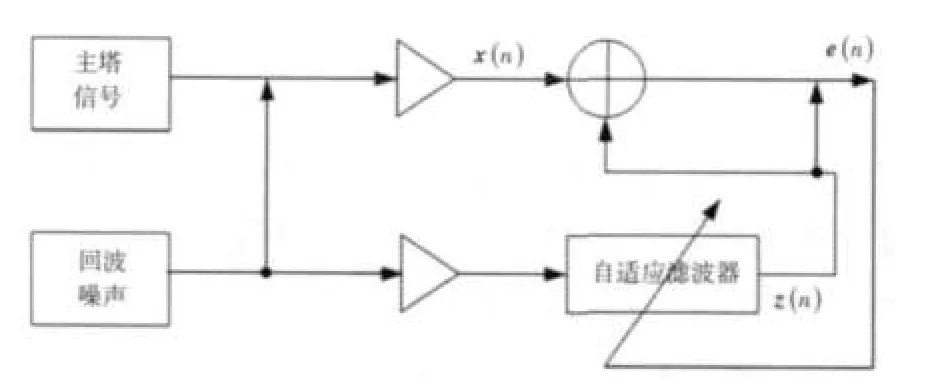
图2 算法原理图

式（10）已证明μ越大，自适应滤波器的收敛数度越快，但是会有较大的失调误差；相反，μ越小，收敛速度越慢，失调误差越小。

3 仿真及结果分析

为了验证该算法的有效性和评估该系统的性能，采用MATLAB中的Simulink进行仿真。

实验一：在设计时还要考虑FIR滤波器的最优长度。理论上更多阶数的FIR滤波器可以消除更加分散的多经，但并不是FIR滤波器的长度越大越好。首先，阶数多时计算误差较大，实现时占用的FPGA资源较多。其次，多径延时非常长，也就是说这个回波是从较远的地方传播回来的，它的传播路径较远，能量较小，消除它的必要性不足。以上两点说明滤波器的长度存在一个最优长度，并非越长越好。在这里通过实验发现当FIR的长度为170～190时残留回波处于一个最小的范围，再结合上面的分析决定选取FIR的长度为175。对应关系如图3所示。

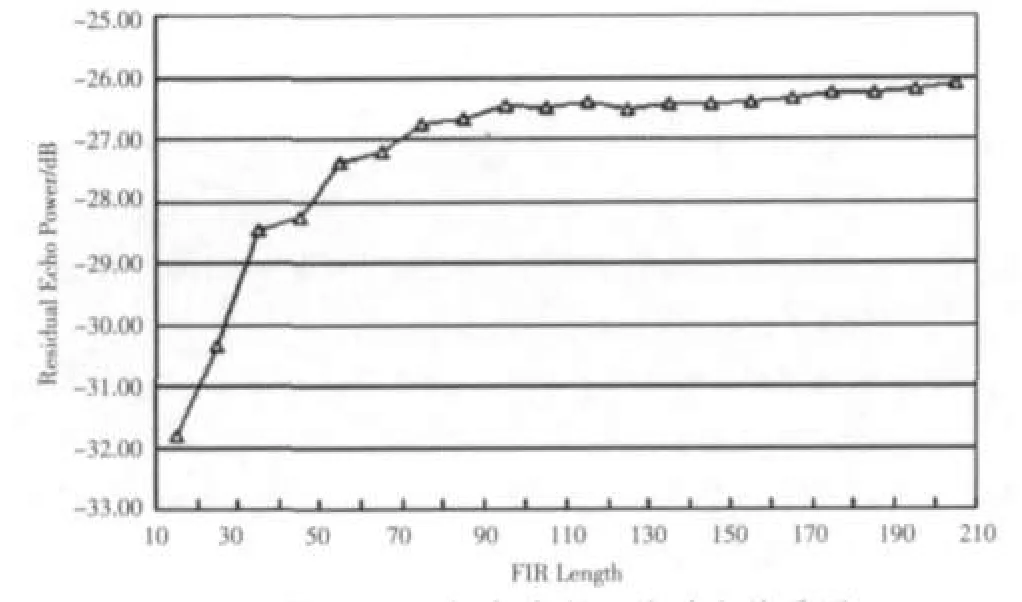
图3 FIR长度残留回波对应关系图

经过分析计算μ的最优取值范围为2-5～2-3，仿真中μ取0.037 7。

实验表明，开启ICS系统后与开启ICS系统前比较，该系统对回波有较好的抑制作用。回波抵消仿真模型如图4所示，结果如图5所示。图5中黄色的波形为回波消除系统开启前的输出波形图，蓝色的为回波消除系统开启后的波形图，实验结果表明该系统可有效消除回波。

实验二：为了进一步了解信噪比与回波消除能力的关系，在FIR长度一样的情况下分别给输入端输入-30 dB，-20 dB，-10 dB的噪声与13.70 dB，13.70 dB，14.12 dB的信号，见表1。得到在信噪比较低的情况下回波消除能力和SNR呈线性关系，在性噪比较高的情况下为非线性关系，如图6所示，图中case1、case2、case3分别代表输入噪声为-10 dB，-20 dB，-30 dB时的情况。

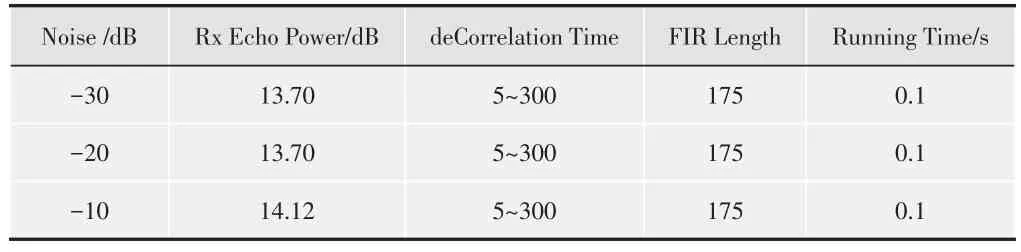
表1 实验二参数情况

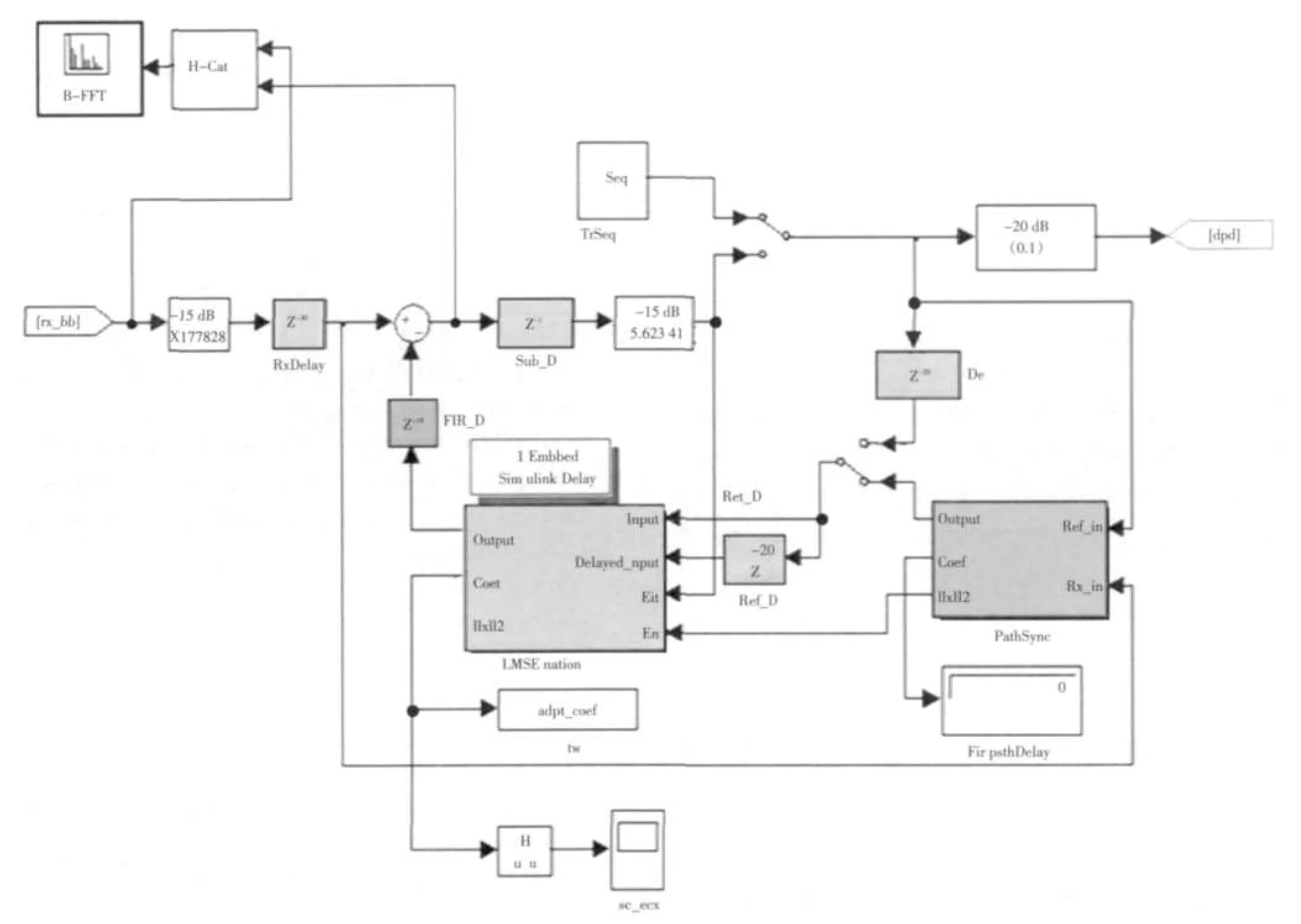
图4 回波抵消仿真模型

图5 开启回波消除系统前后输出波形图（截图）

图6 SNR残留回波对应关系图（截图）

4 结论

本文对基于LMS算法的自适应直放站回波抵消算法进行了研究，结果表明该算法可以有效改善信号的回波对系统的影响，提高系统的稳定性。实验仿真结果表明该算法可有效地消除回波，具有良好的使用价值。

[1] 高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报，2001，29（8）：1094-1097.

[2] 赵春晖，张朝柱.自适应信号处理技术[M].北京：北京理工大学出版社，2009.

[3] 姚天任，孙洪.现代数字信号处理[M].武汉：华中理工大学出版社，1999.

[4] 张园，王辉.基于LMS算法自适应回波抵消器的Simulink仿真分析[J].现代电子技术，2008（17）：101-104.

[5] 周建英.基于LMS算法的智能天线波束形成研究及实现[D].哈尔滨：哈尔滨工程大学，2008.

[6] 李昕.基于FPGA的自适应滤波器设计及在回声消除中的应用研究[D].西安：中国科学院研究生院，2009.

[7]WIDROW B，MCCOOL J M，LARIMORE M G，et al.Stationary and nonstationary learning eharaeteris ics of the LMS adaptive filter[C]//Proc.IEEE.[S.l.]：IEEE Press，1976：1151-1162.

[8] BUTTERWECH H J.A ware theory of long adapive filters[J].IEEE Trans.Circuits and Systems I:Fundamental Theory and Applications,2001，48（6）：739-747.