数学课堂教学“六个反思”的实践与思考——《计数原理I——乘法原理》的教学案例及点评
☉上 海 市 大 同 中 学 张亚东 李 幸
☉上海外国语附属大境中学 李 红
如何提高课堂教学有效性是个比较热门的话题.近年来笔者听了不少数学课,感受最深的是很多年轻老师把数学课上成了“电视讲座”课,缺少师生互动和学生的交流体验过程,被P P T课件牵着鼻子走,大容量、快节奏、填鸭式的应试教学模式大量充斥着课堂,在某种程度上违背了“以学定教”的教学原则.针对这一现状,我们制定了数学课堂教学“六个反思”,并用它来规范自己的教学行为.经过多年来的教学实践,我校数学课堂教学面貌焕然一新,形成了自己的课堂教学特色,大幅度提高了课堂教学效率.本文结合上海市二期课改新教材《计数原理I——乘法原理》一节课的设计与课堂教学,谈谈我们的教学实践与反思,希望对同行们有所启迪.
【附】数学课堂教学“六个反思”一览表

1 预设的问题是否引起学生的回应与思考?2 有没有留给学生思考问题的时间与空间?3 学生能讲、可以讲的,教师讲了或多讲了吗?4 有没有对学生学习行为进行科学的评价?5 有没有对学生的发言引起足够的重视,是顺着学生的思路,还是按照自己的思路?6 有没有发现学生学习的问题或使学生生成新问题,激励学生进一步研究和思考?
师:同学们,很久以前原始人就会利用结绳来计数,我国早在宋代就出现了算盘.计数问题在我们学习生活中随处可见,比如图1中包含五角星的矩形有多少个的问题.计数问题是我们进一步学习排列、组合、概率学、统计学的基础.
图1
点评:这节课是排列组合这一章的开篇课.简短的几句话,几幅漂亮的图片,把学生带进一个崭新的数学世界,激起学生的求知欲望——到底如何计数?排列组合是个什么东西?概率学、统计学到底学什么?上海市二期课改新教材在每一章的开章篇都有类似的文字,这是新教材的一大特色.
师:到底如何计数?它遵循哪些原理?今天我们就来探究计数原理之一——乘法原理,它在日常生活中有着广泛的应用.同学们还记得上周我们去劳技中心,你们思考过这样的问题吗?
问题1:如图2,从学校经公交换乘前往劳技中心有几条不同的行走路线?
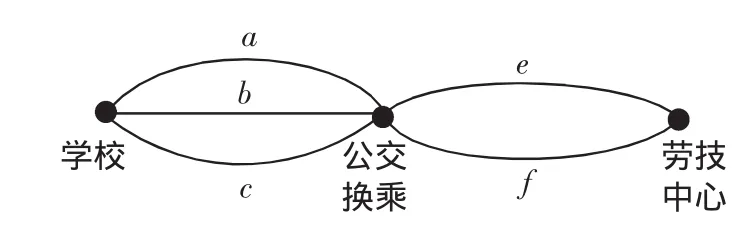
图2
点评:数学就在身边,看你有没有发现的能力,正如牛顿看到苹果掉下来发现了万有引力一样.问题背景非常贴近学生的生活,同学们议论纷纷,预设的问题引起了学生的热烈回应和思考.
生1:应该是6条不同的行走路线.
师:怎么来的呢?
生 1:我是一一数出来的:a-e,a-f;b-e,b-f;c-e,c-f.
师:很好!分类列举也是解决计数问题的基本方法之一,如果数据太大,情况复杂就有点麻烦了.
生2:从学校到劳技中心可分成两个步骤:第一步从学校到公交换乘有3种走法,第二步从公交换乘到劳技中心有2种走法,所以共有3×2=6种不同的走法.
师:非常棒!如果劳技中心有东西两个大门,那么我们从学校出发,经公交换乘再进入劳技中心,共有多少种不同的走法呢?
生3:应该是 3×2×2=12种(如图3).
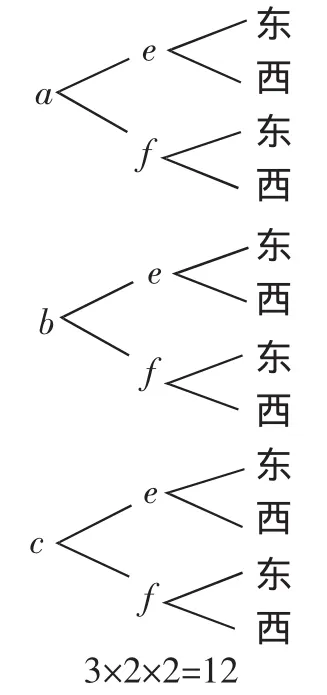
图3
师:有道理,完成这件事需要三步骤……
点评:乘法原理是人们在大量实践经验的基础上归纳出的基本计数原理.本题设计的目的是让学生从简单的问题中体验感悟出乘法原理.这里通过师生互动,教师追问和启发,让学生体验和感悟乘法原理的存在.
师:能不能举一些生活中类似的实例?(学生活动讨论交流)
生4:早上穿衣服(同学窃笑),上装有4件,裤子有3条,袜子有2双,共有4×3×2=24种不同的搭配方案.
生5:中午食堂吃饭,冷菜有3种选择,热炒有5种选择,饮料有2种选择,那么共有3×5×2=30种不同的选择.
生6:祖父的遗传基因分为显性和隐性……
点评:一石激起千层浪.这一精彩的设计思路实际上源于我们的反思2和反思3:要留给学生充分的思考问题的时间和空间;学生能讲的、可以讲的教师不要代替,当然我们的设计要让学生有东西好讲,有感而发,在彼此的思维碰撞中产生灵感,感悟乘法原理的发现过程.
师:看似简单的道理,却蕴藏着深刻的计数原理,谁来概括一下?
生7:完成一件事,需要分成n个步骤,第一步有a种不同的方法;第二步有b种不同的方法……
师:那最多就只有26步了(学生会意地笑).
生7:第一步有a1种不同的方法,第二步有a2种不同的方法,…,第n步有an种不同的方法.那么完成这件事共有N=a1×a2×…×an种不同的方法.
教师板书:

则完成这件事共有N=m1×m2×…×mn种不同的方法
点评:过去我们的做法往往是用PPT直接打出乘法原理,然后让学生跟着读一遍,接着就是大量的训练来熟悉原理.这里教者放手让学生从大量生活中的实例中抽象概括出乘法原理,让学生体会到发现的乐趣.学生在表达过程中可能遇到很多困难,老师顺着学生的思路,重视学生的发言,当他遇到困难的时候,经过教师的启发,其他学生帮忙,在纠错过程中体会原理表述的艰辛,这正是我们的反思5对老师的要求.
师:完成下列事件的方法总数都是3×2=6种吗?(打出PPT如图4)

图4
同学们议论纷纷,争论不休……
生8:它们都违背了乘法原理的分步原则,不符合乘法原理的前提条件,都只有3种不同的方法.
点评:这一设计匠心独到!一个数学概念的理解并不像我们所想象的那样一蹴而就,它有一个螺旋式上升的过程.只有在概念的辨析过程中学生才能真正体会到乘法原理的精髓和本质,纠正错误理解的同时预防机械性的模仿,同时这里还蕴藏着将要学到的加法原理.
师:我们来到了劳技中心的手机组装车间,遇到了新的问题:为统一的机芯设计了2种不同外形同时又有3种不同颜色,还有8G、16G、32G、64G四种不同内存手机配件,该中心共可组装出多少种不同款式的手机?
生 10:2×3×4=24 种.
师:请你对照原理,完成一件什么事,分成几步完成,每步又分别有几种方法?
生11:完成组装手机这件事,分三个步骤,第一步选外形有2种,第二步选颜色有3种,第三步选内存有4种,所以共有2×3×4=24种不同款式的手机.
师:我们又来到手机的测试中心,遇到了第二个问题:手机程序模块中(如图5),一条执行路径就是一条遵循箭头方向、从开始到结束的路径.要测试该程序模块的所有执行路径,共要测试多少次?
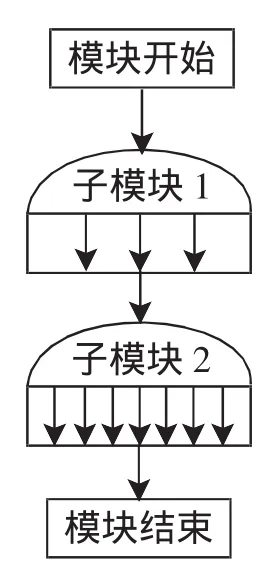
图5
生 12:3×7=21.
师:为何不是3+7=10呢?
生13:因为要完成从开始到结束的路径的测试必须经过两个步骤:第一步有3条,第二步有7条,而每一条路径都只是从开始到结束的一个部分,并不能独立完成这件事,所以根据乘法原理得出共21条不同的测试路径.
点评:教者巧妙利用到劳技中心参加手机研发这一学生非常熟悉的背景故事,把几个问题有机地串联起来,娓娓道来,设计思路实际上源于我们的反思1,让学生真正体会到身边处处是数学.这个问题的设计层层深入,抽象层次逐步提升,让学生体验到灵活运用原理的全部过程.
师:我们在使用手机的时候又遇到设计密码的问题:由0,1,2,…,9十个数字共可设计多少个不同的三位密码?
生14:确定三位密码可分三步,第一步确定百位上的数字有10种选择,第二步确定十位上的数字也有10种选择,第三步确定个位上的数字还是10种选择,所以共可设置10×10×10=1000种不同的三位密码.
师:如果数字不允许重复呢?生 15:共有 10×9×8=720 种.师:如果某人设置的密码为720的正约数,请问这样的密码共有多少个呢?
点评:这是课本上的例题,有一定的挑战性,学生陷入了沉思之中,遇到两个困惑:一是不熟悉什么是正约数,这是初中学过的概念,二是确定正约数不知如何分步,这时就离不开我们老师的正确引导了.
师:同学们,720数据太大,它的正约数也太多,遇到这种问题我们一般怎么办?
生16:退到简单情况摸索规律.
师:很好,不妨我们先来看看12有几个正约数.
生 17:12 的正约数有 1,2,3,4,6,12.
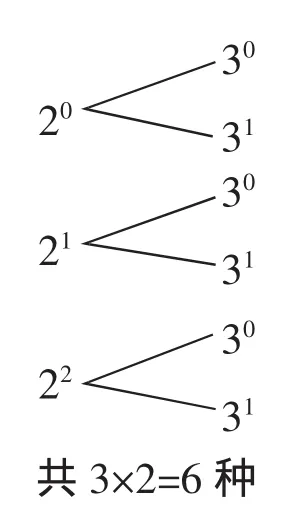
生18:先将12质因数分解成2·2·3=22·3,而 1=20·30,2=21·30,3=20·31,4=22·30,6=21·31,12=22·3;要确定 12 的正约数,可以分两步,第一步确定因数2的个数有0,1,2三种可能,第二步确定因数3的个数有0和1两种可能,所以12的正约数共有3×2=6个.
师:非常好!这一规律可以推广到720吗?
生 19:可以,将 720 质因数分解成 24·32·5,同理可得720 的正约数有(4+1)×(2+1)×(1+1)=30 个.
生20:还可以推广到更一般的结论:如果一个正整数m可分解成··…·,其中p1、p2、…、pn均为互不相等的素数,a1、a2、…、an为正整数,那么m的不同正约数有(1+a1)(1+a2)…(1+an)个.
师:你真聪明!回顾刚才我们解决问题的历程,对你有何启发?
生21:遇到难题先充分地退,退到最简单的情形,通过摸索规律,再推广到一般.
师:非常了不起的想法,这一数学思想方法很重要,它常常是我们开启难题的金钥匙.
点评:对学生的学习行为进行科学的评价能够起到激励作用.这里教师正是利用科学的评价,并激励他们一步一步地把问题进行深化.教师及时发现学生在学习过程中可能遇到的问题,促成学生生成新的问题,在解决问题时体会到乘法原理发现过程中运用到的从一般到特殊,再从特殊到一般的数学思想方法的精要,实在是难能可贵.
师:谁来给今天这堂课进行小结?
生22:今天我们学习了乘法原理,完成一件事需要分成若干个步骤,然后确定每个步骤的方法数,最后将它们乘起来,就得到完成这件事的总的方法数.
师:很好,从处理问题的方法角度对你有何启发呢?
生23:从身边具体事例出发,通过抽象概括提炼出乘法原理,再利用原理去处理各种实际问题,学到了从特殊到一般,再从一般到特殊的处理问题的方法.
师:你觉得运用乘法原理最难的是什么呢?
生24:是确定步骤,有时候步骤不是很明显,需要我们去构造和发现.
生25:老师,我很想知道开头提出的一个计数问题:图中含有五角星的矩形有多少个?初中竞赛的时候我们都是数出来的,不数能算出来吗?
生26(非常得意的):这还不简单,要确定一个含五角星的矩形需要四步:确定矩形左面一边有4种选择,右面一边有3种,上面一边有2种,下面一边有2种,所以共有 4×3×2×2=48 个.
全班同学报以热烈的掌声,成功的喜悦溢于言表.
点评:执教老师通过启发学生从知识和能力两个方面对这堂课进行小结,起到提纲挈领、画龙点睛之效.让学生知道40分钟到底学到了哪些知识,领悟到哪些数学思想方法,学得清清楚楚、明明白白是非常重要的.这一点往往被我们年轻老师所忽视.
【感悟反思】
乘法原理是人们在大量实践经验的基础上归纳出的基本计数原理之一.同时乘法原理又是学习排列组合的理论基础.乘法原理体现的有序思考方法,是把一个复杂问题的解决过程分解为若干“步骤”,先对每个步骤进行细致分析、再整合,最终达到解决问题的目的.
教者通过带领学生去劳技中心组装手机这个熟知的背景故事,将几个典型的例子巧妙地串联起来,以归纳、概括、理解、应用原理为明线,以特殊到一般,又从一般到特殊这一数学思想方法为暗线,通过对特殊事例的归纳、推理,凸显乘法原理发现的过程,在知识的发生发展过程中培养学生的有序思维和归纳概括能力;教师通过精心设计,遵循由简单到复杂,由“有步”到“无步”的循序渐进的教学原则,让学生亲历数学探究的苦与乐,分享发现新知和解决问题的乐趣,提高数学学习的兴趣,及时发现学生学习的问题或使学生生成新问题,激励学生进一步研究和思考.
特别值得一提的是教师在教学设计和教学实施过程中,自觉不自觉地利用“六个反思”规范教学行为.通过巧妙地设计问题背景,放低门槛,引导学生积极参与到教学活动中来,体验数学知识的发生发展过程,激发学生学习数学知识的热情.同时留给学生足够的思考问题的时间和空间,一改教师一言堂的教学模式.通过组织学生讨论,在交流过程中进行思维的碰撞,在不断纠错过程中加深对数学知识和概念的理解和升华,从而锻炼学生的口头表达能力、团队协作以及发现数学真理抽象概括真理的能力,让学生真正参与到教学活动中来.在课堂教学过程中教师跟随学生的思维,通过对学生发言的科学评价,激发学生参与课堂讨论的热情,促成学生生成新的数学问题,从课内探讨延伸到课外研究,一改以课件PPT内容为主导的课堂教学模式,真正体现了“以生为本”的二期课改新理念,大大提高了课堂教学效率,切实减轻学生过重的学业负担和学习压力.
可见,利用“六个反思”来规范我们的数学课堂教学,使全体老师体会到在课堂教学过程中调动学生积极性,激发学生参与教学全过程,在数学概念的发生发展过程中提出问题、遇到困难、解决问题、最后获得成功喜悦,再发生新问题的循环过程中体悟到学习数学的乐趣,真正把“以学定教”的课改新理念融入数学课堂教学的每一个环节,从根本上改变我们的课堂教学面貌,给数学课堂增添绿色.■
- 中学数学杂志的其它文章
- 基于“阅读·引导·提炼·探究”的教学设计:空间几何体的表面积

