起重机伸缩臂最优截面形式的研究
刘 宇,黄 琳
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.大连华锐重工集团股份有限公司,辽宁 大连 116013)
经济的不断发展对装备制造业技术创新与结构升级提出了迫切要求.随着起重机逐渐向大吨位和大起升高度方向的发展,起重机臂架的优化设计已经成为国内外研究人员不可忽视的重要部分[1-3].以德国利勃海尔公司(LIEBHERR)为代表的先进伸缩臂技术,体现了当前世界最高水平,是轮式起重机伸缩臂技术的发展方向[4].LTM1300起重臂的截面采用了椭圆形截面,其截面上弯板为大圆弧槽形板,下弯板为椭圆形槽形板[5];GROVE和TADANO主要采用大圆弧六边形截面.针对现今出现的各类臂架,寻找最优的截面形式,研究臂架截面参数的改变对臂架的综合性能的影响具有重要的现实意义.
本文利用ANSYS有限元分析软件的APDL语言进行二次开发,初步确定截面基本参数,完成臂架参数化建模,针对不同目标函数及约束条件对截面进行优化,分析臂架因截面参数的变化对刚度、强度及稳定性影响程度,从而确定影响臂架结构整体性能的主要因素和相对次要因素,并得出不同条件下的最优截面形式.
1 基于APDL的优化设计
基于APDL的ANSYS有限元优化设计技术是有限元技术的延伸和扩展,ANSYS有限元优化设计技术必须借助APDL语言来实现参数化有限元分析过程.在有限元分析过程中,几乎所有的设计量如厚度、长度、半径等几何尺寸,材料特性、载荷位置及大小等都可以用变量参数表示,通过改变这些变量参数的赋值就能获得不同设计方案的分析结果.在工程应用中,经常需要在保证材料的许用工作范围、结构强度和刚度必须达到足够安全的标准、结构不发生失稳、振动幅值等动力响应指标不超过许用范围等的前提条件下,使质量、面积、体积、应力、费用等达到极小化.ANSYS基于有限元分析的优化设计就是在满足设计要求的条件下搜索最优设计方案.
优化设计是寻求最合理的设计方案,而优化方法则是实现优化设计的手段.所谓优化方法是使目标函数在控制条件下达到最小值的传统化方法.结构优化问题大多属于约束优化问题.根据对约束条件的处理方法的不同,约束优化方法可以分为两大类:零阶方法和一阶方法.零阶方法是优化设计中应用较多的方法.它的基本思想是采用目标函数和约束条件的逼近方法,对目标函数添加罚函数将有约束优化问题转化成无约束优化问题,通过迭代使目标函数逼近最小值,它是一个很完善的处理方法,可以有效地解决大多数的工程问题.其数学函数描述为近似式:

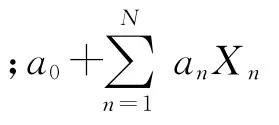
在ANSYS软件中采用Design Opt>Method/Tool>Sub-problem方法,可以对近似式中的变量进行调整:增加目标函数,即增加式(1)中的二次项和交叉项,增加状态变量,即仅增加二次项,增加设计变量的范围,即增加线性项.
在优化设计初始时,需要几个设计集,以形成近似式.再利用ANSYS产生的随机设计,或利用优化数据库中的现成设计,提供已知的“好的”设计来改进近似精度[6],最后保留可行域内或最好的设计方案.零阶近似法作为通用方法,能够迅速获得优化结果.
2 伸缩臂截面参数尺寸优化的数学模型
2.1 伸缩臂截面优化参数的选择
为了得到最合理的设计方案,本文将臂架截面设置了几个基本参数.对初始截面形状为U形的臂架截面基本参数(如图1所示),具体含义说明如下:L1为臂架中性截面宽度;H1为臂架中性截面高度;t1为上翼缘板厚度;t2为下翼缘板厚度;R1为上翼缘板折弯半径;H2为下翼缘板开始折弯处高度;H3为下翼缘板高度.
最终建立初始有限元截面模型如图2所示.

图1 臂架截面基本参数显示图Fig.1 Displaying graph of boom-section basic parameters

图2 初始有限元模型Fig.2 Initial finite element model
2.2 伸缩臂截面约束条件的建立
用材料力学方法建立的伸缩臂约束条件虽然简单,但建立的数学模型不完全符合结构的力学特性,而且各节臂之间的重叠部分还不是目标函数的设计变量,以致影响吊臂的轻量化,而采用有限元法可避免上述缺陷[7].
采用有限元法中的空间梁单元所组成的总刚度方程为
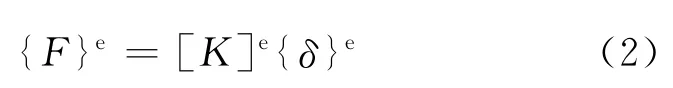
式中:{F}e为单元节点力,{F}e=[Fzi,Fyi,Fxi,Mzi,Myi,Mxi,Fzj,Fyj,Fxj]T,Fzi,Fyi,Fxi为i节点在z,y,x3个方向上的节点力,Mzi,Myi,Mxi为i节点在z,y,x3个方向上的力矩,Fzj,Fyj,Fxj为j节点在z,y,x3个方向上的节点力;[K]e为单元刚度矩阵;{δ}e为单元节点位移,{δ}e=[wi,vi,ui,φzi,φyi,φxi,wj,vj,uj,φzj,φyj,φxj]T,wi,vi,ui和wj,vj,uj分别为i,j节点在z,y,x3个方向上的位移量,φzi,φyi,φxi和φzj,φyj,φxj分别为i,j节点在z,y,x3个方向上的转角.
箱形吊臂的边界条件为:根部铰点和变幅油缸上的铰点在变幅平面yz内为简支;在回转平面xz内呈固支,吊臂的顶端为自由端,各臂段之间的滑块结点在y方向上的转角为零.
最后利用结点力求应力:

式中:Ai为i节点处截面面积.

式中:τzi为i节点在z方向上的剪应力;G为切变模量;J为截面的极惯性矩;Wk为抗扭截面系数.
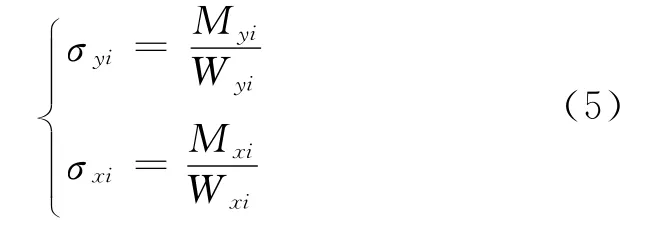
式中:σyi,σxi分别为i节点在y,x方向的应力;Wyi,Wxi分别为i节点所在臂架截面对y,x轴的截面模量.
由上述诸应力,求得吊臂最大节点应力为
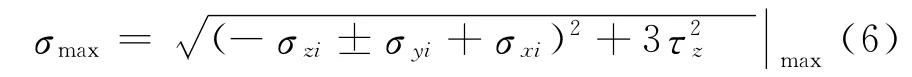
于是,用有限元法建立的吊臂强度约束函数为

式中:[σ]为许用应力.
2.3 伸缩臂截面目标函数的确定
根据伸缩臂结构设计的各项指标,本文选择臂架的质量作为目标函数.也就是说,在满足约束条件下,使臂架质量最小.选用ANSYS中的参数化设计语言APDL编制优化程序并对伸缩臂进行结构优化设计.由于ANSYS软件本身的一些模块可以方便地计算和提取臂架的质量,这样在优化循环过程中,每搜索到一个可行点,程序会自动给出相应的臂架质量,从而有利于优化设计的程序化计算.
3 伸缩臂参数化模型的建立与优化
伸缩臂截面的参数化设计及优化过程是借助ANSYS有限元分析软件操作平台完成的.具体步骤如下:
(1)在前处理器PREP7中建立参数化模型.定义设计变量为L1,H1,t1,t2,R1,H2.臂长设为常量,其值为10m.密度设置为7.8×10-6kg·mm-3,抗弯模量Ex=210GPa,泊松比为μ=0.3.选用shell63板单元来模拟臂架结构.
(2)在求解器SOLUTION中加载并求解.为了探讨臂架受力对臂架各参数及其形状的影响,边界条件的确定是非常重要的.根据起重机伸缩臂的工作原理,可知臂架之间的受力的传递主要通过每节臂的支撑滑块来实现的.因此在有限元分析过程中采用面力的形式将臂架间的受力施加在前后滑块处.根据臂架在工作过程中在变幅平面内为外伸梁、在回转平面内为悬臂梁的工程实际,当采用有限元法进行臂架分析时,在臂架的根部施加3个方向的位移约束,及2个方向的转动约束,在变幅油缸处施加2个方向的位移约束.模拟重力加速度对臂架的作用实现臂架自重的加载,具体实现公式为

式中:gx和gz分别为重力加速度在x,z方向上的分量,α1为臂架仰角.
(3)在后处理器POST1/POST26中提取并指定状态变量和目标函数.采用APDL访问ANSYS数据库,提取模型和结果信息,并依据提取的信息定义状态变量和目标函数变量.本例要求将总质量作为目标函数,假定密度是恒定的,从数据库中提取总体积,通过换算得到总质量并将其作为目标函数,将计算得到的总应力最大值作为状态变量.
(4)执行优化过程.将臂架截面参数作为初值进行尺寸优化,具体见表1.在计算机系统中查找分析文件并读入,执行一次完整分析过程,设置设计变量及状态变量的取值范围.对目标函数和状态变量整体变化进行评估,采用子问题法作为优化工具最终得出状态变量对目标函数影响的规律.

表1 臂架初始参数Tab.1 Initial parameters of boom
4 伸缩臂优化结果
通过优化分析,可得到表2中的5个参数对臂架性能主要参数的影响趋势.由表2可知:

表2 5个参数对臂架性能的影响趋势Tab.2 Affecting trend of boom capability when five parameters changed
(1)臂架性能各参数在上翼缘板折弯半径R1、下翼缘板折弯处高度H2、臂架宽度L1的已设定区间内是单调函数.
(2)下翼缘板高度对最大综合应力σmax和屈曲稳定性系数a的影响趋势恰恰相反.
(3)要达到臂架自重减小的效果,需要在满足应力约束、位移约束、屈曲稳定性约束的前提下,适当地增加上翼缘板的折弯半径和下翼缘板折弯处的高度,减小臂架高度、臂架宽度.
综上所述,如何合理选择参数的大小,使它们之间的组合最为合理,将是优化设计中需要关注的问题.
将表2中5个参数同时改变,查看臂架性能和臂架屈曲稳定性的变化过程,分别得到相应的迭代曲线,如图3,4所示.由图3,4可以看出:

图3 臂架性能迭代曲线Fig.3 Iterative curve of boom capability
(1)随着迭代步数的逐渐增加,臂架各性能参数最终稳定在某一值上,即迭代收敛.
(2)臂架自重的变化趋势与臂架的最大应力的变化趋势恰恰相反.因此在设计中尤其要注意二者兼顾.
(3)臂架屈曲稳定性系数的取值在迭代到第25步时到达最大,而此时最大应力值较小,但臂架自重出现了第5个波峰,臂架自重达到整个迭代过程中的最大值.由此可见,在设计中应根据实际情况对屈曲稳定性系数、臂架自重及最大应力三者作适当选取.
从迭代过程中节选出应力最小时的臂架截面形状图(如图5)、屈曲稳定性系数最大时的臂架截面图(如图6)、质量最轻时的臂架截面形状图(如图7)和综合位移最小时的臂架截面图(如图8).
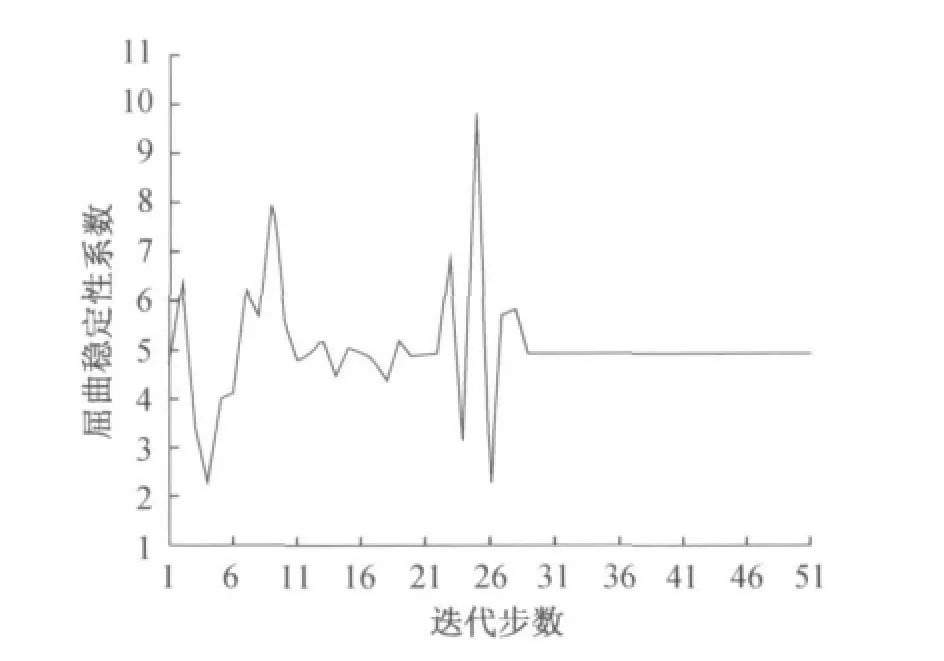
图4 臂架屈曲稳定性系数迭代曲线Fig.4 Iterative curve of inflectional stability coefficient of boom

图5 应力最小时的臂架截面图Fig.5 Boom-section sketch under minimal stress
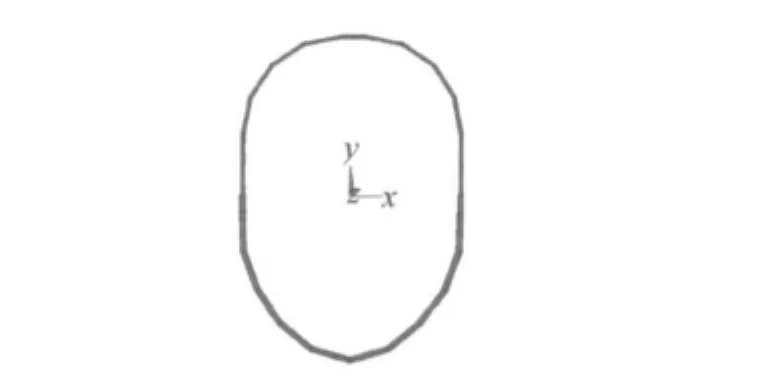
图6 屈曲系数最大时的臂架截面图Fig.6 Boom-section sketch under maximal inflectional coefficient

图7 重质最轻时的臂架截面图Fig.7 Boom-section sketch under minimalminimal weight

图8 综合位移最小时的臂架截面图Fig.8 Boom-section sketch under displacement vector sum

表3 各极值状态下的臂架性能参数Tab.3 Parameters of boom capability under different extreme value condition
由优化迭代结果得出各极值状态下的臂架性能参数,如表3所示.从图5~8及表3可以看出:
为了满足应力最小、变形最小的条件,设计者可以适当地采用趋向于大U形截面,如图5和8.为了满足质量最轻、追求结构的稳定性要求,设计人员可以适当地采用趋向于鸭蛋形截面,如图6和7所示.
5 结论
本文利用ANSYS有限元分析软件分析不同臂架截面参数变化对臂架刚度、强度及稳定性的影响规律,总结了截面参数的变化趋势对臂架综合性能指标的影响,并根据影响程度的不同,设置优化敏感参数,由此对伸缩臂结构模型进行性能参数优化,得出不同约束条件下的最优截面形式.理论验证了U形截面吊臂应力小、变形小的结构特点以及鸭蛋形截面吊臂重量轻、结构稳定性好的结构特点,为起重机臂架截面的设计提供了参考.
[1]滕儒民,刘阚元,陈礼.有限元法计算大吨位伸缩臂起重机起重性能[J].中国工程机械学报,2011,9(2):194-199.
TENG Rumin,LIU Kanyuan,CHEN Li.FEM calculation for hoisting performance of large-tonnage telescopic boom cranes[J].Chinese Journal of Construction Machinery,2011,9(2):194-199.
[2]刘士明,陆念力,寇捷.起重机箱形伸缩臂整体稳定性分析[J].中国工程机械学报,2010,8(1):29-34.
LIU Shiming,LU Nianli,KOU Jie.Global stability analysis on crane telescopic boom[J].Chinese Journal of Construction Machinery,2010,8(1):29-34.
[3]牟瑞平,张硕.起重机伸缩臂局部稳定性研究[J].中国工程机械学报,2008,6(2):171-174.
MOU Ruiping,ZHANG Shuo.Local stability study on crane telescopic boom [J].Chinese Journal of Construction Machinery,2008,6(2):171-174.
[4]王笑世,李军.浅谈利勃海尔400t起重机伸缩臂内油缸锁定及解锁[J].甘肃科技纵横,2011,40(4):39-41.
WANG Xiaoshi,LI Jun.Talk about locking and unlocking of the cylinder in telescopic boom of LTM1400crane[J].Gansu Science and Technology,2011,40(4):39-41.
[5]卓先领.探析国产全地面起重机未来之路[J].建筑机械化,2005,(8):8-9.
ZHUO Xianling.Analysis of the future of Chinese all-terrain crane[J].Construction Mechanization.2005(8):8-9.
[6]黄翼卓.钢框架体系优化设计研究[D].上海:同济大学,2006.
HUANG jizhuo.Study on optimal design of steel frame systems[D].Shanghai:Tongji University,2006.
[7]张质文,虞和谦,王金诺,等.起重机设计手册[M].北京:中国铁道出版社,2001.
ZHANG Zhiwen,YU Heqian,WANG Jinnuo,et al.Crane’s design handbook[M].Beijing:China Railway Press,2001.

