电动助力转向系统随动特性仿真
陈 克,万思彤,李 铎
(沈阳理工大学 汽车与交通学院,辽宁 沈阳 110159)
EPS电动助力转向系统,是一种目前应用广泛的汽车动力转向技术.随着微电子控制技术在汽车领域的广泛使用,以及世界节能环保两大主题的推广,EPS的优越性越来越突出,成为转向技术研究的重点和热点内容[1].EPS系统必须随时根据驾驶员的操作,提供渐进随动的转向助力动作,所以系统必须有很高的跟踪性能,很好的稳定性、鲁棒性等.
在早期EPS系统研究与开发中,采用较多的一种控制方法是:采用PID控制器对助力电机电流进行闭环控制,来实现EPS系统的助力控制[2].传统PID控制器结构简单,具有一定的鲁棒性,容易实现,稳态无静差,控制精度高[3].但PID电流控制方法存在以下问题:PID参数只能通过大量试验获得,不易获得最优的参数;系统抗干扰性能较差,容易产生转向振动,转向路感不易调整等[4].传统的PID控制并不能够很好地解决EPS系统的非线性问题[5].只能在系统参数固定不变的情况下基本满足控制要求,无法处理系统的不确定性.为了克服传统PID电流控制方法的不足,本文将模糊控制理论思想与传统的PID控制相结合,设计出模糊自适应PID控制器.在动态过程中实时在线调整PID参数,增强了系统的稳定性指标.
1 EPS系统动力学模型
根据电动机布置位置的不同,EPS系统可分为转向轴助力式、齿轮助力式和齿条助力式3种类型,本文研究转向轴式助力式.EPS系统主要包括机械式转向器、转矩传感器、减速机构、离合器、电动机、电子控制单元(Electronic Control Unit,ECU)和车速传感器等.
将复杂的EPS系统简化为只包含转向盘和转向轴、电机、齿轮齿条机构、转向前轮组件4个重要动力学元件的EPS物理模型.物理模型如图1所示.图中,θc为转向盘转角位移;Jc为转向盘转动惯量;bc为转向盘阻尼系数;Kc为转矩传感器扭转刚度;G为电动机减速机构传动比;Jm为电动机及蜗杆传动惯量;θm为电动机转角;Tm为电动机提供的助力转矩;bm为电机阻尼系数;Km为电机传动轴刚度;ro为小齿轮半径;mr为齿条和车轮的等效质量;br为齿条阻尼系数;xr为齿条位移;Fr为转向机构与前轮等效到齿轮齿条上的转向阻力;NL为等效到前轮的转向器传动比;K1为转向机构与前轮等效到下端转向轴的前轮侧偏刚度;b1为转向机构与前轮等效到下端转向轴阻尼系数;δ为前轮转角.
为了建立EPS系统的动力学模型,将物理模型继续简化,分成3个组件:转向盘转向轴组件、电机组件和齿轮齿条组件.
描述这3个组件的运动变量分别是:转向盘转角位移θc,电机转角位移θm,齿条平移位移Xr.考虑EPS系统的转动惯量J、刚度K和阻尼系数b,对各组件进行受力分析,根据牛顿定理,建立EPS系统动力学模型.
(1)转向盘转向轴组件动力学模型

式中:Ts为转矩传感器检测到的力矩;Td为转向盘输入转矩.
(2)电机组件动力学模型

式中:L为电机电枢电感;R为电机电枢电阻;i为电机电流;Kf为电机反电动势系数;u为电机电压;Kt为电动机转矩系数.
(3)齿轮齿条组件动力学模型

式中:mr为齿条和车轮的等效质量;Kr为回转力矩弹性系数.

图1 EPS的简化物理模型Fig.1 Eimplified physical model of EPS
2 模糊自适应PID控制策略
EPS系统控制策略主要解决两个问题:一是确定系统的助力特性;二是采用何种方法能够快速地、稳定地跟踪该助力特性.助力特性是指助力随汽车运动状况(车速和转向盘手力)变化而变化的规律[6].助力与电机电流的大小成比例.本文将着重讨论如何实现对助力特性快速稳定的跟踪,即电机电流能否对目标电流具有良好的跟随性.
PID控制器由比例单元P、积分单元I和微分单元D组成.其控制器的组成框图如图2所示.图中输入值r(t)与实际输出反馈值c(t)构成控制偏差e(t),即e(t)=r(t)-c(t),u(t)为经过PID控制器调整后被控对象两端电枢电压.PID控制器主要适用于基本线性和动态特性不随时间变化的系统,其比例环节系数Kp、积分环节系数Ki、微分环节系数Kd是确定不可变的.而汽车EPS系统随时受到外界随机性因素影响,如果PID的3个参数可根据不同的情况按照一定的规律适时调整,即可提高系统的响应速度,减低超调量.所以本文将模糊控制理论与PID控制理论相结合,使车辆在不同工况下可实时在线调整PID控制器的3个参数,以提高系统的稳定性能指标.
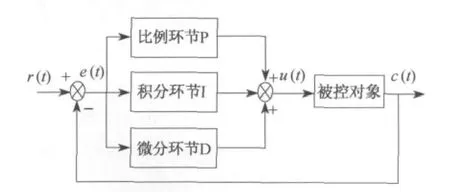
图2 PID控制器的组成框图Fig.2 PID controller composition block diagram
模糊控制器为单变量二维模糊控制器,以电流传感器测得的电流值I为变量,二维输入量均为实际电流采样值Ie与目标电流Io的差值e及差值变化率ec,输出为ΔKp,ΔKi及ΔKd.PID参数模糊自整定是先找出PID 3个参数与e和ec之间的模糊关系,在工作中通过不断检测e和ec,再根据模糊控制原理来对3个参数进行在线校正,以满足不同e和ec时对控制参数的不同要求,而使被控对象有良好的动、静态性能[7].模糊自适应PID控制器的结构如图3所示.

图3 模糊自适应PID控制器结构图Fig.3 Fuzzy adaptive PID controller schematic diagram
2.1 模糊控制规则的建立
本文设计模糊自适应PID控制器不采用微分,故只考虑Kp与Ki在不同时刻的作用和相互之间的关系.比例系数Kp的作用是加快系统的响应速度,提高系统的调节精度.Kp越大,系统的响应速度越快,系统的调节精度越高,但易产生超调,甚至会导致系统不稳定;Kp取值过小,则会降低调节精度,使响应速度缓慢,从而延长调节时间,使系统静态、动态特性变坏.积分系数Ki的作用是消除系统的稳态误差.Ki越大,系统的静态误差消除得越快,但Ki越大,在响应过程的初期会产生积分饱和现象,从而引起响应过程的较大超调;若Ki过小,将使系统的静态误差难以消除,影响系统的调节精度.针对不同的e和ec,整定Kp和Ki原则如下:
(1)Kp整定原则.电动机刚开始助力时,|e|很大,无论|ec|如何,都应增大Kp,以加快系统响应速度;当助力稳定,|e|处于中等大小时,为减小系统超调应减小Kp;在助力后期,|e|接近于0时,ec为负,则减小Kp,ec接近于0或为正时增大Kp.
(2)Ki整定原则.当|e|较大时,为了避免系统响应出现较大超调,应对积分作用加以限制,通常取Ki取较小值;在|e|和|ec|中等大小时,取适当Ki;|e|较小时,Ki可取大些.
将e,ec,ΔKp,ΔKi的变化范围定义为模糊论域上的模糊子集,为{NB,NM,NS,ZO,PS,PM,PB}.子集中的元素分别代表{负大,负中,负小,零,正小,正中,正大}.模糊论域e,ec,ΔKp,ΔKi={-3,-2,-1,0,1,2,3}.Kp,Ki整定的模糊规则表,见表1.

表1 模糊控制规则表Tab.1 Fuzzy control rule tabulation
系统经过模糊化、模糊推理和解模糊化后,得到比例系数和积分系数的增量ΔKp,ΔKi,分别与PID设定的初始值Kp0,Ki0相加,得到最终的校正量Kp=Kp0+ΔKp,Ki=Ki0+ΔKi.
3 软件仿真
运用仿真软件MATLAB 7.0进行仿真运算.设定PID参数初值Kp0=30,Ki0=400,Kd0=0.e,ec,ΔKp,ΔKi的量化因子分别为5,0.0015,3.3,133.EPS系统仿真算法流程图,如图4所示.

图4 EPS系统仿真算法流程图Fig.4 System simulation algorithm flow chart of EPS
根据EPS系统动力学模型建立仿真模型,为验证模糊自适应PID控制器对目标电流的跟踪效果,分别在车速0,30,60,90km·h-1下对系统输入阶跃信号,以模仿驾驶员快速转动方向盘的情况,在车速30,90km·h-1下对系统输入正弦信号,以模仿驾驶员常速转动方向盘的情况,输出信号均为电机电流.电机电流控制器分别采用传统PID控制策略和模糊自适应PID控制策略对电流进行闭环控制.得到电机电流阶跃响应曲线和电机电流正弦响应曲线,如图5,6所示.

图5 电机电流阶跃响应曲线Fig.5 Motor current step response curve

图6 电机电流正弦响应曲线Fig.6 Motor current sine response curve
图5为电机电流Im对阶跃信号的响应,可以看出在车速为0,30,60,90km·h-1时,在快速转动方向盘的情况下,采用模糊自适应PID控制器的调节时间比传统PID控制器均快约0.02s.2种控制器的电流响应超调量见表2.从表2中的数据的对比看出模糊自适应PID控制器的响应超调量均小于传统PID控制器的响应超调量.这表明采用模糊自适应PID控制器后,电机电流的随动性能明显提高,即系统的稳定性与可靠性得到改善.
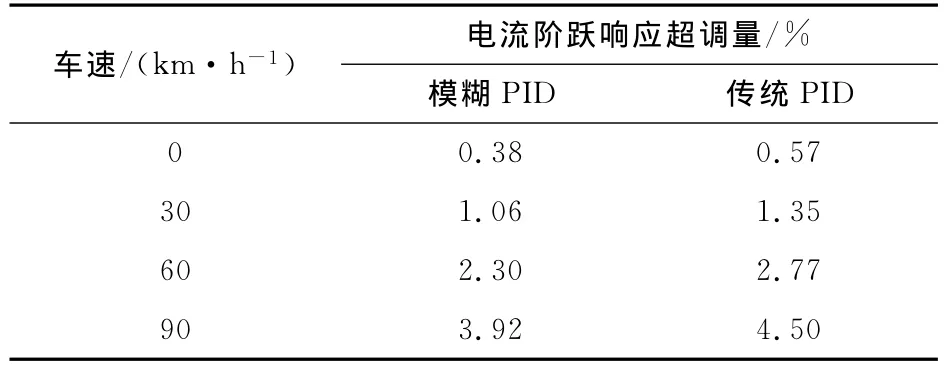
表2 电机电流阶跃响应超调量对比Tab.2 Motor current step response overshoot contrast
图6中,电机电流Im对正弦信号的响应,常速转动方向盘的情况下两控制结果曲线几乎重合在一起,两控制方法的响应时间和调节时间基本相同.模糊自适应PID控制器对电流跟踪效果略好于传统PID控制器.在车速为30km·h-1时,模糊自适应PID控制器的响应超调量比传统PID控制器下降约37.5%;在车速为90km·h-1时,模糊自适应PID控制器的响应超调量比传统PID控制器下降约8.8%.
4 结论
本文针对汽车EPS系统进行研究,建立其动力学模型,为增强电机电流对目标电流的随动性能,提出模糊自适应PID控制策略,并进行仿真计算.结果表明,采用传统PID控制策略和模糊自适应PID控制策略,电机电流对目标电流的跟踪性都取得了良好的效果,但采用模糊自适应PID控制策略所得到的电机实际电流对目标电流的跟踪性更好,响应超调量比传统PID控制器降低30%左右.在动态过程中改变PID的参数,发挥了二者的优点,改善了EPS系统的动态响应、操纵平稳、高跟踪性等各项指标.
[1]雷琼红.电动助力转向(EPS)技术的现状和发展趋势分析[J].机械工程师,2009(9):53-55.
LEI Qionghong.Current status and development tendency analysis of automobile electrical power steering system[J].Mechanical Engineer,2009(9):53-55.
[2]KIM J H, SONG J B.Control logic for an electric power steering system using assist motor[J].Mechatronics,2002,12(3):447-459.
[3]殷云华,樊水康,陈闽鄂.自适应模糊PID控制器的设计和仿真[J].火力与指挥控制,2008,33(7):96-99.
YIN Yunhua,FAN Shuikang,CHEN Mine.The design and simulation of adaptive fuzzy PID controller[J].Firepower and Command and Control,2008,33(7):96-99.
[4]杨水卜.电动助力转向系统的建模与控制方法研究[D].哈尔滨:哈尔滨工业大学,2009.
YANG Shuibo.Modeling and control research for electric power steering system [D].Harbin:Harbin Institute of Technology University,2009.
[5]熊建桥,唐小琦,陈吉红.基于模糊控制策略的EPS设计与实现[J].计算机工程与应用,2007,43(34):101-104.
XIONG Jianqiao,TANG Xiaoqi,CHEN Jihong.EPS design and realization based on fuzzy control strategy[J].Computer and Engineering and Application,2007,43(34):101-104.
[6]周廷明,刘志辉,李梦奇,等.电动助力转向系统及其关键技术[J].机床与液压,2012,40(4):176-179.
ZHOU Tingming,LIU Zhihui,LI Mengqi,et al.Electronic power steering system and its key technologies[J].Machine Tool & Hydraulics,2012,40(4):176-179.
[7]姚绪梁,赵云凯,尹国慧.基于模糊控制器的直流无刷电动机控制[J].控制工程,2009,16(5):346-349.
YAO Xuliang,ZHAO Yunkai,YIN Guohui.Control of brushless DC motor based on fuzzy controller[J].Control Engineering of China,2009,16(5):346-349.

