基于航迹无关模型的传感器系统误差可观测性分析

朱洪伟 唐小明 何 友*



基于航迹无关模型的传感器系统误差可观测性分析

朱洪伟 唐小明 何 友

(海军航空工程学院电子信息工程系 烟台 264001)

可观测性分析是建立系统误差估计模型的一个必要前提。针对系统误差航迹无关估计模型的可观测性问题，该文采用可观测矩阵研究系统误差的可观测性和可观测度。首先建立了基于航迹无关的系统误差量测与状态转换模型，在此基础上构建了系统误差的可观测矩阵，通过判定可观测矩阵的奇异性研究了系统误差的可观测性问题，并且给出了可观测度的表达式，最后建立了典型的仿真环境，分析了可观测度对系统误差估计精度的影响以及传感器的几何位置和目标的运动状态对系统可观测性及可观测度的影响。

可观测性；可观测度；可观测矩阵；系统误差估计；航迹无关模型

1 引言

传感器探测系统自身存在的定位系统误差以及在使用过程中不可避免地产生的距离、距离增益、方位、俯仰等测量系统误差，会使得各传感器对目标的状态估计偏离真实值，很可能导致融合跟踪系统对同一个目标生成多条航迹，或者融合后丢失目标，造成航迹关联混乱、融合精度降低，进而使整体系统融合失去意义。因此系统误差配准是多传感器信息融合的必然前提。

常用的多传感器配准算法是根据多个传感器对在其公共观测区域内同一目标的量测建立配准模型并采用相应的估计算法对模型求解。在实际应用中，很多系统误差估计算法需要知道目标的真实位置，但是目标的真实位置往往很难得到，因此这些算法均采用量测或者对位置的估计来近似目标的真实位置，使得系统误差的估计精度不高，进而影响到整个融合系统的性能。而基于航迹无关模型的系统误差估计模型通过两部传感器的量测消除目标真实位置的影响，并构建系统误差的伪量测方程，将系统误差向量作为系统的状态向量来建立误差估计模型。这种模型的优点是误差估计算法中并不需要知道目标的真实位置，从而能够大大提高系统误差的估计精度。国内外有很多文献研究了基于航迹无关模型的系统误差估计算法，如实时质量控制(Real Time Quality Control, RTQC)误差估计算法，广义最小二乘-实时质量控制(Generalized Least Squares-RTQC, GLS-RTQC) 误差估计算法，最小二乘(Least Squares) 误差估计算法，广义最小二乘(Generalized Least Squares)误差配准算法，以及基于卡尔曼滤波的实时误差配准算法。但是这些研究在构建系统误差估计模型时均假定系统误差是可观测的，并没有对系统误差的可观测性进行分析与研究。一方面，在理论算法研究中，对于已经构建的误差估计模型，可观测性分析能够确定模型中的状态向量是否可观测、可观测的条件以及可观测的强弱程度。另一方面，在实际应用中，当存在多个目标的量测时，通过系统误差的可观测强弱分析，可以选取系统误差可观测程度较强的目标的量测来估计系统误差，以提高系统误差估计算法的效率以及精度。因此可观测性分析是建立有效的系统误差估计模型的一个必要前提。只有确认系统误差在模型中是可观测的，进一步建立的误差估计模型才有意义。而目前国内外的相关研究很少，因此针对系统误差的可观测性分析进行研究具有重要的意义。

文献[18,19]利用Fisher信息矩阵的行列式作为可观测矩阵来研究目标状态的可观测性问题。借鉴目标状态的可观测性研究方法，本文在建立航迹无关误差估计模型的基础上，利用可观测矩阵研究系统误差的可观测性，同时给出系统误差的可观测度以及可观测的条件，并通过仿真来分析系统误差可观测性以及可观测度的特点。

2 航迹无关的系统误差估计模型

受系统误差的影响，传感器量测会偏离目标的真实位置，如图1所示。

由图1可以得到传感器,的量测分别为：

图1 系统误差下传感器量测示意图

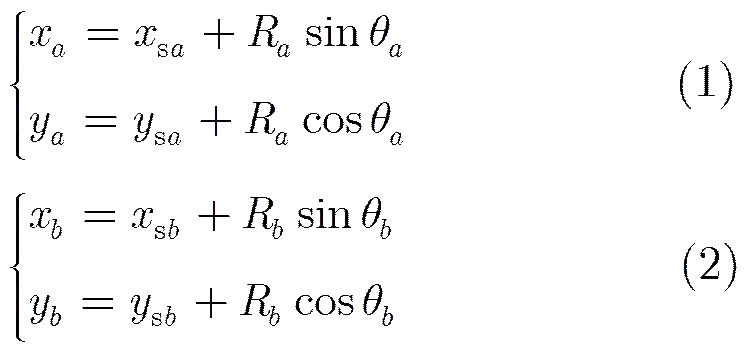
假如有

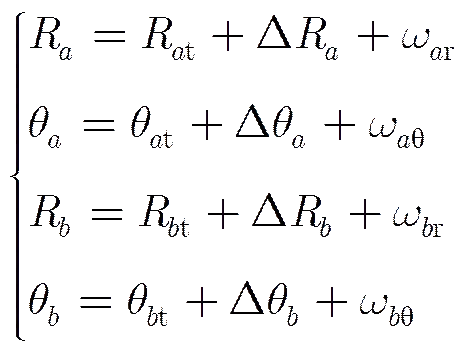
(4)

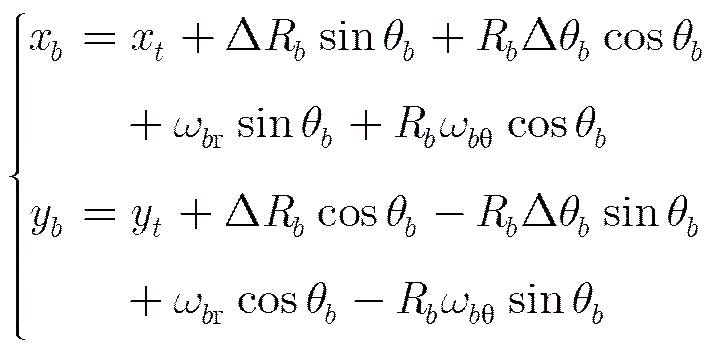
(6)

其中伪量测向量

(8)

伪量测矩阵

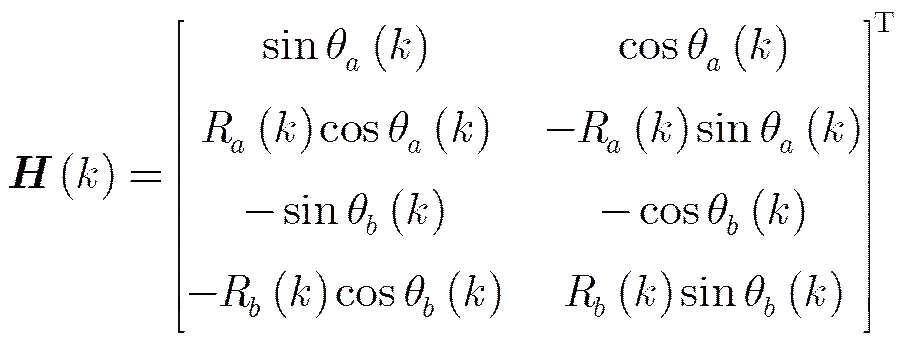
系统误差状态向量

(10)

量测噪声

再假定系统误差是固定量，则系统误差的状态模型为：

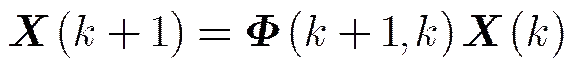
3 系统误差可观测性分析

由于理论上传感器的量测误差不影响可观测性的分析，因此可以忽略量测误差的影响。根据式(7)和式(12)，由参考文献[18]可以得到系统误差的可观测矩阵为：

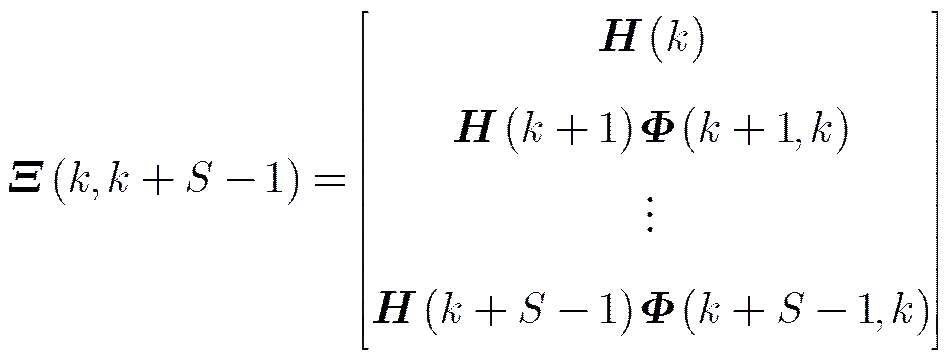
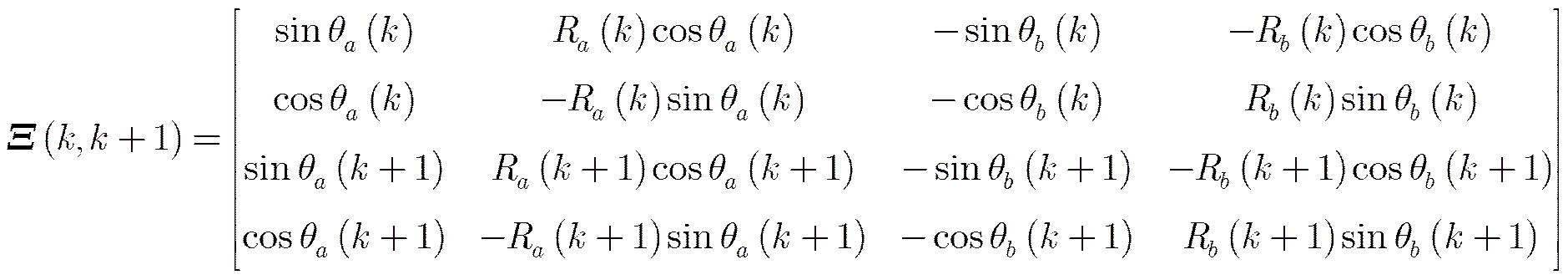
对于式(15)，理想情况下，考虑目标在两部传感器的公共观测区域内运动，所以当，即目标在两部传感器的连线上运动时，。其它条件下，均有。

系统误差的可观测性分析给出了系统误差是否可观测，而系统误差的可观测度则定量地描述系统误差可观测的程度。是状态不确定超椭球体积倒数的量度，因此定义系统误差的可观测度为：

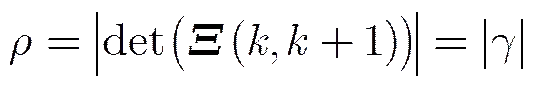
这里需要注意的是，当传感器不存在系统误差时，系统误差可观测的充分必要条件为：

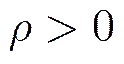
但是在实际应用中，传感器必定会存在一定的系统误差，因此在计算系统误差的可观测度时必须考虑量测误差的影响，此时，系统误差可观测性的充分必要条件为：

(18)

4 仿真分析

通过对可观测度的定量分析，可以找出系统误差可观测度对系统误差估计精度的影响以及目标的运动状态对系统误差可观测度的影响。

4.1 可观测度对系统误差估计精度的影响

假设两部传感器,分别位于原点,。传感器的采样周期为1 s，有关传感器的其它参数如表1所示。为了方便比较，本文的仿真中，对式(16)给出的可观测度作如下处理：

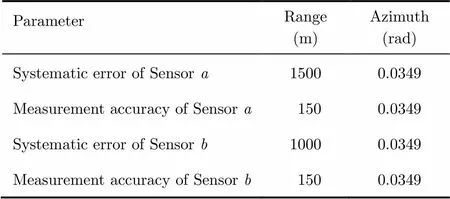
表1 传感器参数

假定有3个目标,,，其坐标方程分别为：

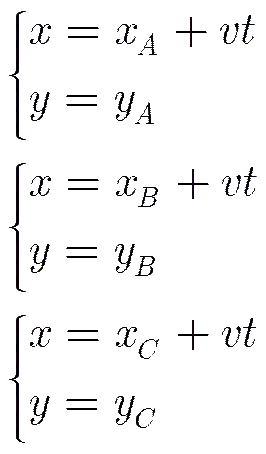
应用式(19)分别计算出目标为,,时系统误差的可观测度，如图3所示。

为了比较应用目标,,来估计系统误差时的精度，采用文献[10]给出的最小二乘算法，估计结果如表2所示，其中Monte Carlo仿真次数为100次。

表2 分别应用目标A, B, C的系统误差估计结果

从图3可以看出，目标的可观测度大于目标,，目标的可观测度大于目标，而从表2给出的估计结果可以看出，目标时系统误差估计结果的精度远远高于目标,时，目标时系统误差估计结果的精度又远远高于目标时，因此可以得出，系统误差的可观测度越大，系统误差的估计精度越高。

4.2 目标运动状态对误差估计系统的影响

为分析目标运动状态对系统误差可观测性的影响，假定4种典型的目标运动方式。

目标运动方式1与两部传感器的连线平行，其坐标方程为：

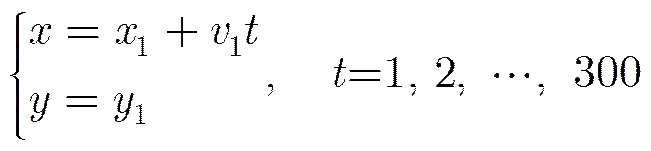
图2 目标, , 运动轨迹

Fig. 2 Tracks of Targets , ,

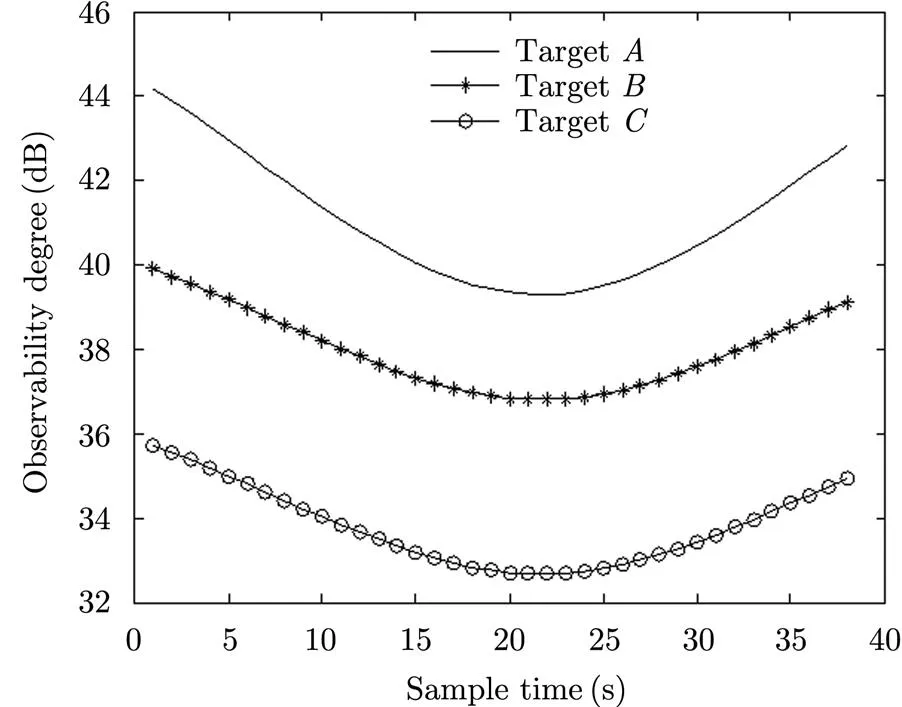
图3 目标A, B, C可观测度比较

从图4和图5可以看出，随着目标越来越接近两部传感器连线的中线时，系统误差的可观测度越来越小，当目标到达中线位置时，可观测度最小，接下来系统误差的可观测程度又越来越强。系统误差的可观测度相对于两传感器连线的中线呈对称分布。

目标运动方式2为两部传感器连线的中线，其坐标方程为：

从图6和图7可以看出，随着目标逐渐靠近两部传感器的连线，系统误差的可观测度逐渐增大，当目标位于240 s左右，即处于两部传感器的连线附近时，系统误差的可观测度达到最大，当目标远离两部传感器的连线运动时，系统误差的可观测度随之逐渐减小。系统误差的可观测度相对于两部传感器的连线呈对称分布。另外，当目标处于传感器连线上时的时刻为，此时如果没有系统误差的存在，则，系统误差的可观测度为0，但是由于系统误差的存在，使得，因此时刻系统误差的可观测度不为0；而当时刻，目标已经不在两部传感器连线上，由于系统误差的可观测度由两个时刻决定，因此反而在穿越点处有最大值出现。

目标运动方式3为两部传感器的连线，其坐标方程为：

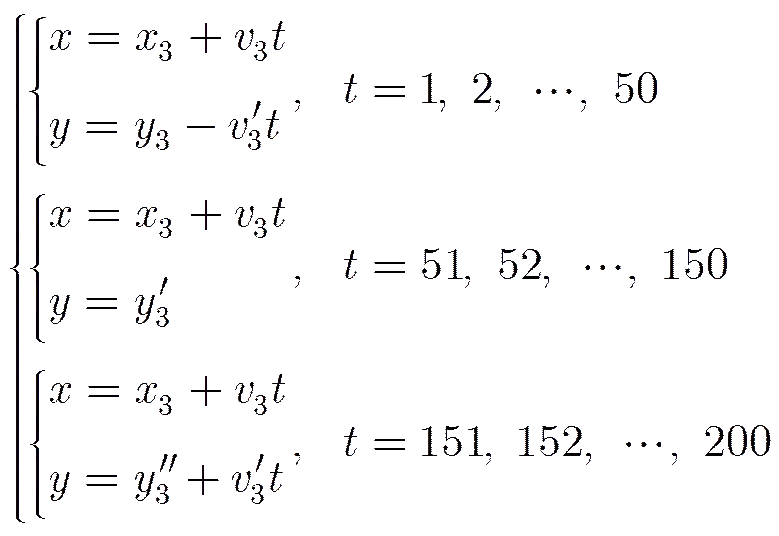
图4 运动方式1的轨迹

Fig. 4 Trajectory of moving Type 1

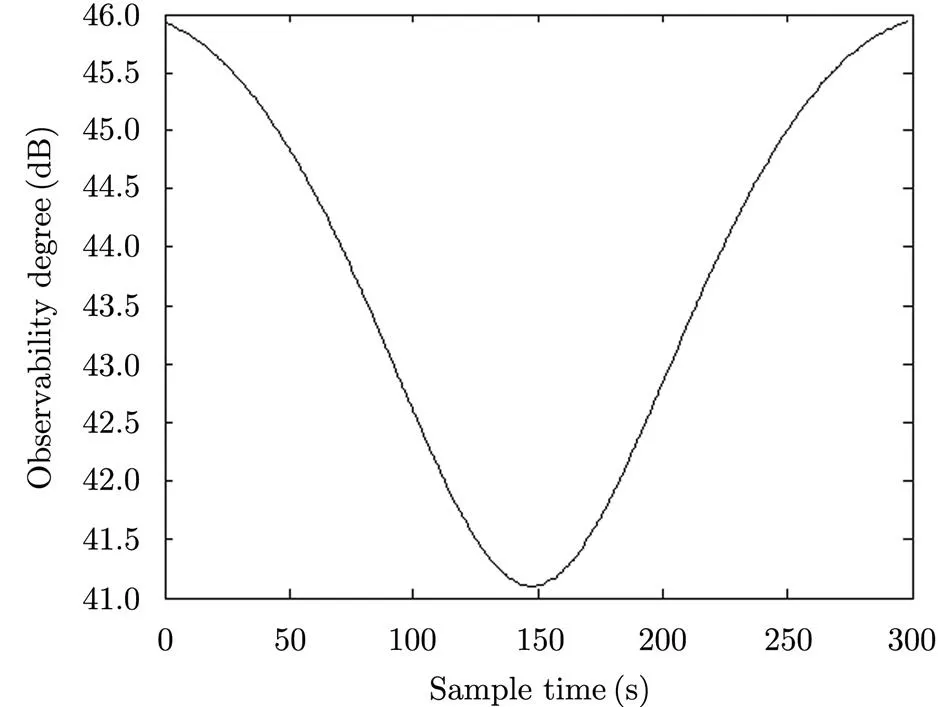
图5 目标运动方式1下系统误差的可观测度

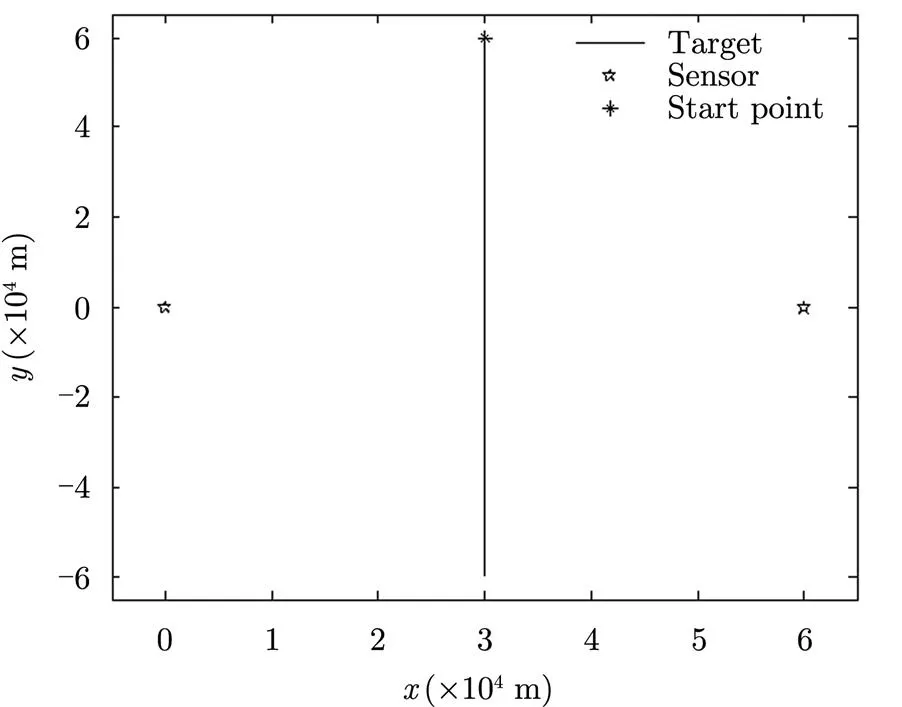
图6 目标运动方式2的轨迹

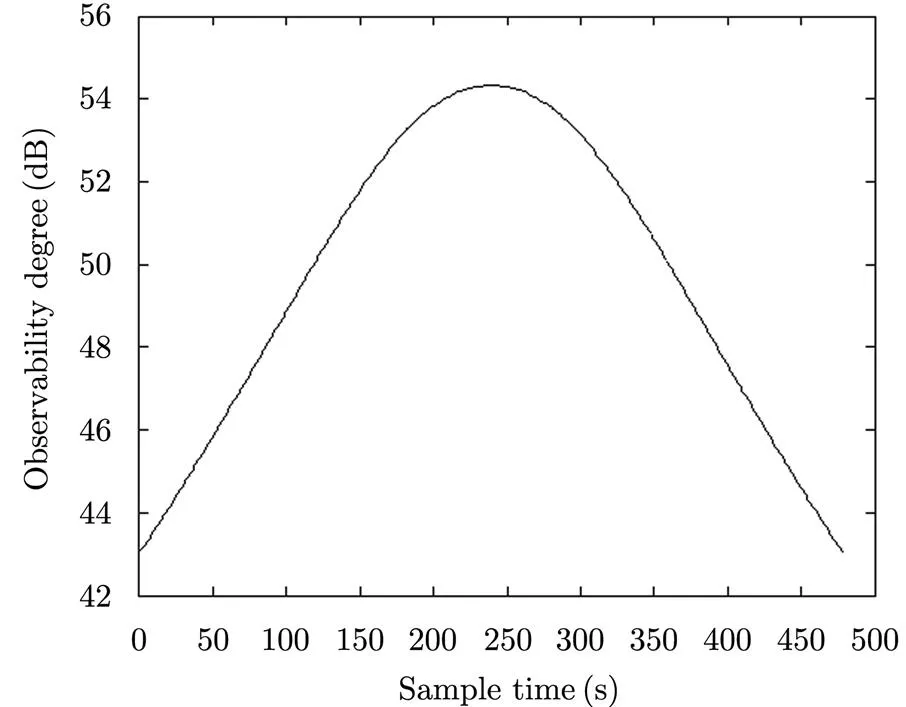
图7 目标运动方式2下系统误差的可观测度

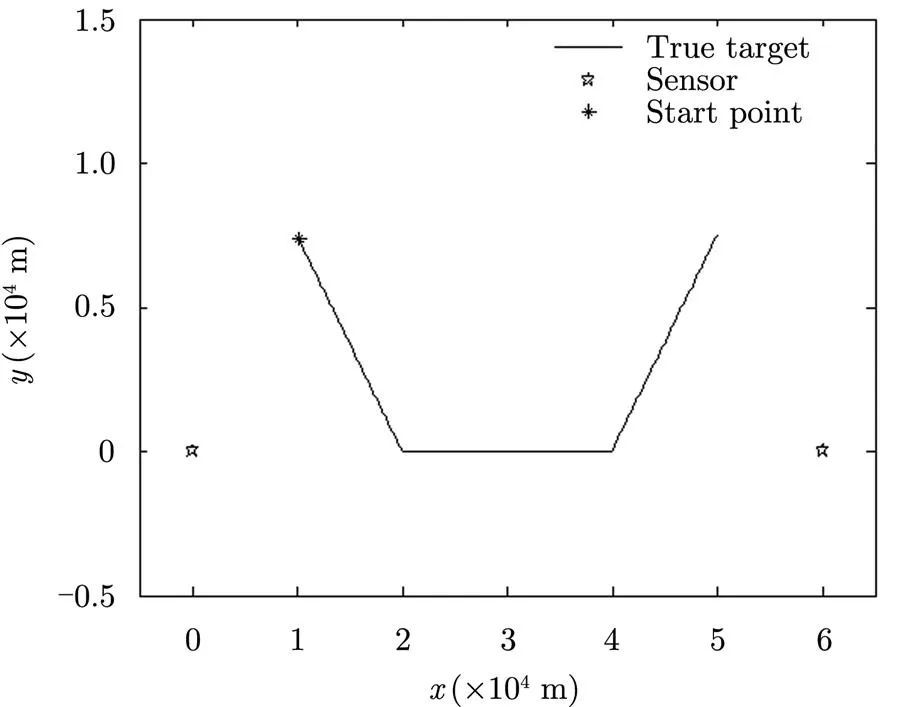
图8 目标运动方式3的轨迹

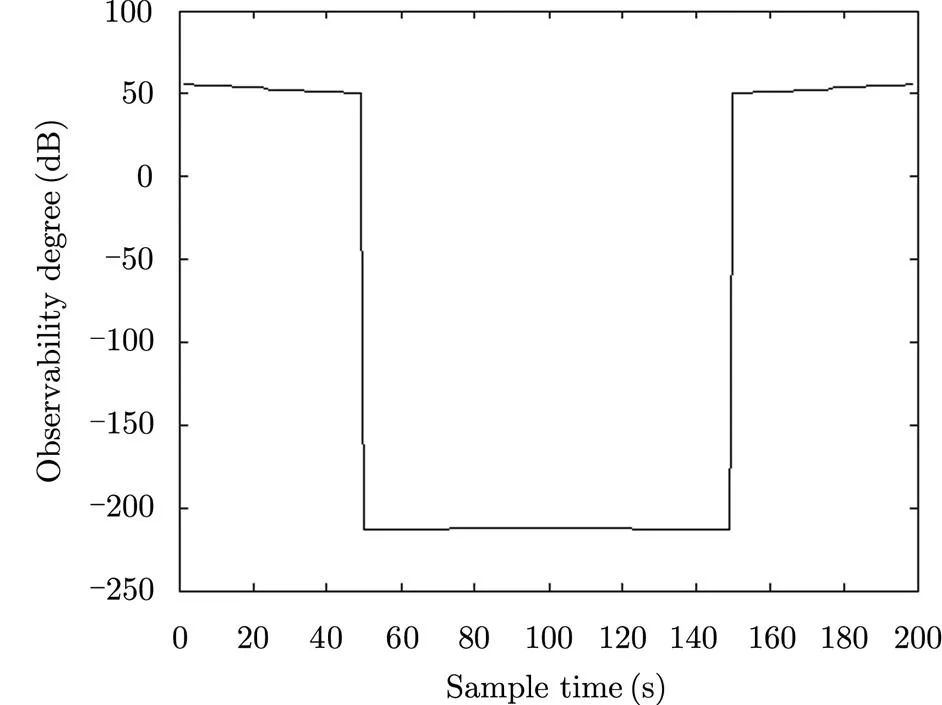
图9 目标运动方式3下系统误差的可观测度

从图8和图9可以看出，当目标在两部传感器的连线上运动时，系统误差的可观测度明显减小，由于系统误差本身的影响，所以可观测度趋近于零。

从图5、图7和图9综合来看，当目标向着两部传感器的连线或者两部传感器连线的中线运动时，系统误差的可观测度逐渐减小，当处于两部传感器的连线或者两部传感器连线的中线时，系统误差的可观测度达到最小。这说明，目标处于两部传感器的连线或者两部传感器连线的中线时，系统误差的可观测程度很弱，不利于系统误差的估计，实际应用中需要尽量避免这种情况的出现，以提高系统误差估计的效率。

5 结论

系统误差估计是多传感器信息融合中的一个难题，而系统误差的可观测分析对系统误差能否很好地估计有着重要的影响。通过系统误差的可观测性分析能够为系统误差估计提供目标最优航迹的选择准则，并可在相同环境和参数设置下通过空间航迹的优选最大程度的提高算法的估计精度和效率。本文研究了2维平面中基于航迹无关的系统误差估计模型中系统误差的可观性问题，并且通过仿真分析了传感器的几何位置和目标的运动状态对误差估计系统的影响，结合实际应用特点，给出了实际中构建误差估计模型来估计系统误差时需要注意的问题。研究系统的可观测性问题可以帮助建立有效的系统误差估计模型以及实现可靠的实际应用。在本文的研究基础上，可以进一步对组网传感器系统中系统误差在公共观测区域的空间分布，即对系统误差场进行研究。

[1] 何友, 宋强, 熊伟. 基于傅里叶变换的航迹对准关联算法[J]. 航空学报, 2010, 31(2): 356-362.

He You, Song Qiang, and Xiong Wei. Track alignment- correlation technique based on phase correlation[J]., 2010, 31(2): 356-362.

[2] 宋强, 崔亚奇, 何友. 反馈式多目标多传感器系统误差融合估计技术[J]. 宇航学报, 2011, 32(1): 115-122.

Song Qiang, Cui Ya-qi, and He You. Multi-target multi- sensor systematic error fusion estimation technique with feedback[J]., 2011, 32(1): 115-122.

[3] Huang D L and Leung H. Maximum likelihood state estimation of Semi-Markovian switching system in non- Gaussian measurement noise[J]., 2010, 46(1): 133-146.

[4] Li Z H, Chen S Y, Leung H,.. Joint data association, registration, and fusion using EM-KF[J]., 2010, 46(2): 496-507.

[5] Lian F, Han C, Liu W,.. Joint spatial registration and multi-target tracking using an extended probability hypothesis density filter[J].,&, 2011, 5(4): 441-448.

[6] Besada J A, Miguel G D, Bernardos A M,.. Generic multisensor multitarget bias estimation architecture[J].,&, 2012, 6(5): 365-378.

[7] Burke J J. The SAGE real time quality control function and its interface with BUIC II/BUIC III[R]. MITRE Corporation Technical Report, No. 308, 1996.

[8] 王波, 王灿林, 董云龙. RTQC 误差配准算法性能分析[J]. 系统仿真学报, 2006, 18(11): 3067-3069, 3081.

Wang Bo, Wang Can-lin, and Dong Yun-long. Analysis of performance of RTQC registration algorithm[J]., 2006, 18(11): 3067-3069, 3081.

[9] 董云龙, 何友, 王国宏, 等. 一种改进的系统偏差估计算法[J]. 宇航学报, 2005, 26(6): 737-742.

Dong Yun-long, He You, Wang Guo-hong,.. One modified algorithms to estimate system errors[J]., 2005, 26(6): 737-742.

[10] Stefano F A F, Fulvio G, Antonio G,.. Least squares estimation and Cramér-Rao type lower bounds for relative sensor registration process[J]., 2011, 59(3): 1075-1087.

[11] Zhou Y F, Leung H, and Blachette M. Sensor alignment with earth-centered earth-fixed (ECEF) coordinate system[J]., 1999, 35(12): 410-418.

[12] 董云龙, 何友, 王国宏, 等. 基于ECEF 的广义最小二乘误差配准技术[J]. 航空学报, 2006, 27(3): 463-467.

Dong Yun-long, He You, Wang Guo-hong,.. Generalized least squares registration algorithm with earth-centered earth-fixed (ECEF) coordinate system[J]., 2006, 27(3): 463-467.

[13] 王波, 王灿林, 李冬. 一种基于Kalman滤波的实时校准算法[J].电子科技大学学报, 2007, 36(5): 872-875.

Wang Bo, Wang Can-lin, and Li Dong. A real-time alignment algorithm based on Kalman filter[J]., 2007, 36(5): 872-875.

[14] 吴泽民, 任姝婕, 刘熹. 传感器系统误差协同配准算法研究[J].兵工学报, 2008, 29(10): 1192-1196.

Wu Ze-min, Ren Shu-jie, and Liu Xi. Research on collaborative registration algorithm for radar system error[J]., 2008, 29(10): 1192-1196.

[15] 熊伟, 潘旭东, 彭应宁, 等. 基于不敏变换的动基座传感器偏差估计方法[J]. 航空学报, 2010, 31(4): 819-824.

Xiong Wei, Pan Xu-dong, Peng Ying-ning,.. Unscented bias estimation technique for maneuvering sensor[J]., 2010, 31(4): 819-824.

[16] Linthotage D L P, Wijerupage S W, and Martin D A. SLAM with joint sensor bias estimation: closed form solutions on observability, error bounds and convergence rates[J]., 2010, 18(3): 732-740.

[17] Agostino M. State estimation based on the concept of continuous symmetry and observability analysis: the case of calibration[J]., 2011, 27(2): 239-255.

[18] 孙仲康, 周一宇, 何黎星. 单多基地有源无源定位技术[M]. 北京: 国防工业出版社, 1996: 196-233.

Sun Zhong-kang, Zhou Yi-yu, and He Li-xing. Location Technology for Single/Multiple Base with Active and Passive Sensors[M]. Beijing: National Defense Industry Press, 1996: 196-233.

[19] Bar-Shalom Y, Li X R, and Kirubarajan T. Estimation with Applications to Tracking and Navigation[M]. New York: John Wiley & Sons, Inc, 2001.

[20] Xiao Y C, Wei P, and Yuan T. Observability and performance analysis of bi/multi-static Doppler-only radar [J]., 2010, 46(4): 1654-1667.

[21] Sinpyo H C, Kwon S H, and Lee M H. Observability measures and their application to GPS/INS[J]., 2008, 57(1): 97-106.

Observability Analysis of Sensor Bias Based onthe Track-independent Model

Zhu Hong-wei Tang Xiao-ming He You

(Institute of Electronics and Information Engineering Naval Aeronautical and Astronautical University, Yantai 264001, China)

In this paper, an observability analysis of sensor bias based on the track-independent estimation model is presented. Observability analysis is a prerequisite for developing a systematic error estimation model. Therefore, an observability matrix is adopted to study the observability and observability degree of sensor bias. Initially, based on the track-independent model, both state transformation and measurement models of sensor bias are built in two dimensions to construct the observability matrix. Then, the observability of the sensor bias is studied by judging the singularity of the observability matrix. Further, the mathematical expression for the degree of observability is presented. Finally, several typical simulations to demonstrate the effect of degree of observability on the estimation accuracy of sensor bias and the effects of sensor location and target motion on the observability and observability degree of sensor bias are provided.

Observability; Observability degree; Observability matrix; Sensor bias estimation; Track-independent estimation model

TN957

A

2095-283X(2013)04-0454-07

10.3724/SP.J.1300.2013.13068

2013-07-23收到，2013-10-25改回；2013-11-08网络优先出版

国家自然科学基金(61032001)和国家自然科学基金青年基金(61102166)资助课题

何友 hjhy_heyou@163.com

朱洪伟(1984-)，男，四川大竹人，博士研究生，工作单位海军航空工程学院，研究方向为传感器系统误差分析与估计。

E-mail: zhuhongwei907@163.com

唐小明(1974-)，男，浙江淳安人，海军航空工程学院副教授，研究方向为传感器系统误差配准系统总体设计与应用。

E-mail: signalfusion@sina.com

何 友(1956-)，男，吉林磐石人，海军航空工程学院教授，主要研究方向为多源信息融合。

E-mail: hjhy_heyou@163.com