A SIFT Algorithm for Bistatic SAR Imaging in a Spaceborne Constant-offset Configuration

Chen Shi-chao* Xing Meng-dao Zhang Shuang-xi Bao Zheng



A SIFT Algorithm for Bistatic SAR Imaging in a Spaceborne Constant-offset Configuration

Chen Shi-chaoXing Meng-dao Zhang Shuang-xi Bao Zheng

(Key Laboratory for Radar Signal Processing, Xidian University, Xi’an 710071, China)

This paper focuses on the problem of the space-variance of the range-cell migration term for bistatic Synthetic Aperture Radar (SAR) and proposes a Scaled Inverse Fourier Transform (SIFT)-based imaging algorithm for the constant-offset configuration of bistatic SAR data processing. Range-cell migration correction is realized when two times phase multiplies and a convolution operation are executed. Because the imaging algorithm is based on a precise spectrum that has been deduced from the Geometry-Based Formula (GBF) algorithm, the proposed algorithm can handle the bistatic SAR data, which were obtained with a large baseline to ratio. The advantages and effectiveness of the proposed imaging method have been verified by simulated and comparable experiments. Moreover, unlike other scaling-imaging algorithms that are dependent on the frequency modulated characteristics of the signal, the SIFT imaging algorithm is also suitable for phase-coded signals, which are used in a wider range of applications.

Bistatic Synthetic Aperture Radar (SAR); 2D Point Target (PT) spectrum; Scaled Inverse Fourier Transform (SIFT)

1 Introduction

Unlike the Synthetic Aperture Radar (SAR) for monostatic case, the transmitter and the receiver of bistatic SAR are mounted on different platforms, and hence results in many great advantages over monostatic SAR. It has a bright future in many application areas such as resource investigation, lithosphere transmutationreconnaissance. Spaceborne constant-offset bistatic SAR has a relatively easy configuration, which can achieve more angular information and improve thedetection probability for Ground Moving Target Indication (GMTI) and can also improve the precision for ground height measurement. Due to its significance, the very configuration has attracted increasing radar workers to work deep into it. And the famous TanDEM- X satellite has been launched already, which has obtained satisfying bistatic SAR imaging results.

As is well known to us, the main difference between the bistatic SAR and the monostatic SAR lie in their different range histories. The range history of the bistatic SAR is the sum of two Double Square Root (DSR), which results in the difficulty of obtaining the precise bistatic Point Target (PT) spectrum by directly using the Principle Of the Stationary Phase (POSP). Although the time domain method can get ideal focusing qualities for general configurations, it requires heavy computational burden. To reduce the com- putational burden of the time domain method, an effective way has been proposed called Fast Factorized Back-Projection (FFBP) algorithm, and Rodriguez- Cassola has extended the FFBP algorithm into bistatic case successfully with the imaging algorithm named Bistatic Fast Factorized Back-Projection (BFFBP) algorithm. However, the computational burden is still heavy respect to the frequency domain algorithms.

The bistatic PT spectrum is the presupposition of designing fast imaging algorithms in the frequency domain, hence, many approximate spectrums have been proposed for bistatic imaging, and many effective imaging algorithms have been proposed for different configurations based on these spectrums. Although these spectrums are all with high precision, and some of them have wider application ranges, they are all approximate ones under different situations. And they can not deal with the bistatic SAR data with large baselines. With the increasing of the baseline, the precision of the spectrums will reduce, and some of them are even very sensitive to the length of the baseline.

Based on the instantaneous Doppler concept, Zhang,. proposed the Geometry-Based Formula (GBF) bistatic PT spectrum for bistatic SAR data processing in parallel configuration, and also gave out a Range Migration Algorithm (RMA) for bistatic stripmap SAR data processing. The analytical expression of the PT spectrum is given in Ref. [24], but an important factor existed in the spectrum is not exact analytically deduced, which has to be gotten through numerical methods. Due to the importance of the constant- offset configuration of bistatic SAR, the exact analytical PT expression has been deduced in Ref. [27], and in which also the corresponding RMA is performed. However, “stolt” interpolation needs to be carried out for the RMA imaging algorithm, the interpolation process requires relatively huge computa- tional burden, and the error caused by the interpolation will also affect the precision of the final image phase, which will give a negative influence to the following process such as the interferometric SAR.

The scaled inverse Fourier transform is performed in the two-Dimensional (2-D) frequency domain to equalize the range-dependence of the range migration term in the SIFT algorithm, the whole imaging process can be finished with only the Fast Fourier Transforms (FFTs) and phase multiplies, the algorithm is with high efficacy and precision. In the same time, the Scaled Inverse Fourier Transform (SIFT) algorithm does not relay on the frequency modulated characteristic of the chirp signal, it can be extended to a more widely range of signal types, such as phase-coded signals.

A SIFT imaging algorithm based on the exact analytical spectrum presented in Ref. [27] for constant- offset configuration bistatic SAR data processing is proposed in this article. The proposed imaging algorithm is suitable for dealing with large baseline bistatic SAR data. Unlike the imaging algorithms in the wavenumber domain, fast imaging algorithm is achieved in the frequency domain. Simulated experi- ment and comparable experiment further verify the effectiveness and advantage of the proposed algorithm.

2 Signal Model of the Constant-offset Bistatic SAR

Fig. 1 shows the geometry relationship of space- borne constant-offset configuration, the transmitter and the receiver moves along the same direction of theaxis (the positive direction of axis) with an identical velocity,andare the instantaneous angles from the target to the transmitter and receiver at zero azimuth time when the transmitter and the receiver are at the locationsand, respectively.andare the corresponding slant ranges, respectively.his half the length of the baseline, andRis the closest distance from the target to the flight path.() and() are the slant ranges of the transmitter and the receiver when they move overdistance away from the zero time positions,andare the corresponding squint angles when the transmitter and the receiver are at locationsand, respectively. Based on the geometry relationship of Fig. 1, the exact analytical solution of the half bistatic angle is deduced successfully through the solution of a four-order equation with the variable of the tangent of the half bistatic angle. The expression is given as:

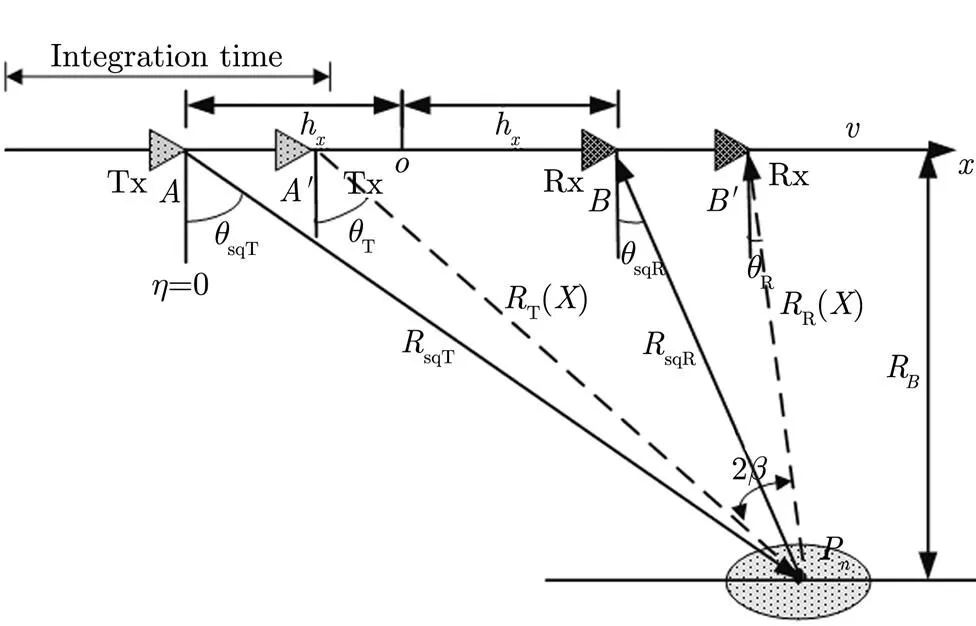
Fig. 1 Illustration of the spaceborne constant-offset bistatic SAR geometry

(2)

From Fig. 1, we can tell that the slant range of the bistatic SAR is

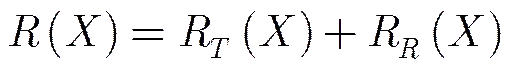
where

Suppose that the radar transmits chirps, and after demodulation and range compression, the signal can be written as

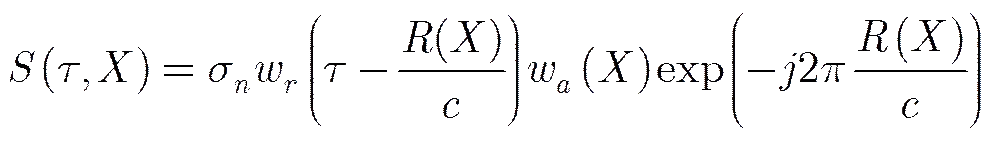
Transforming the signal into thedomain, we have

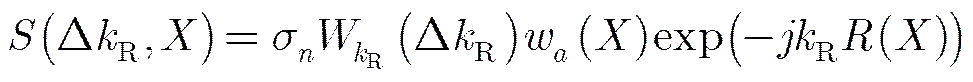
Performing FFT in azimuth to the signal expressed by Eq. (6), we can get the bistatic PT spectrum of the bistatic SAR, which can be expressed as

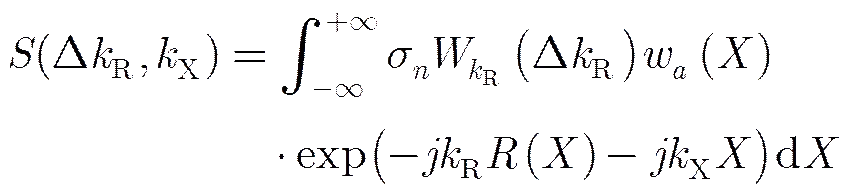
Unfortunately, due to the existence of the DSR term existed in the range history of bistatic SAR, we can not get the exact solution of Eq. (7) by directly using POSP.

3 SIFT Imaging Algorithm for Bistatic SAR in Constant-offset Configuration

Utilizing the GBF method presented in Refs. [24,25], we can get the exact analytical PT spectrum expression of the bistatic SAR. The PT spectrum can be written as

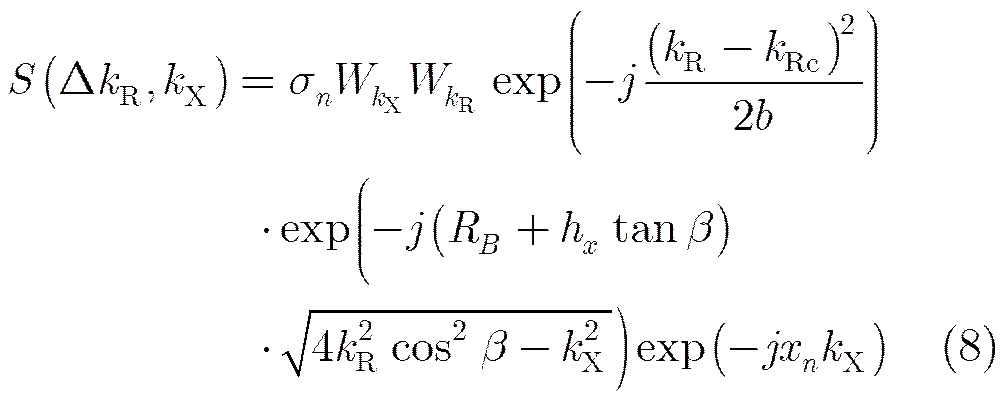
Substituting the half bistatic angle expressed by Eq. (1) and Eq. (2) into Eq. (8), we get the exact analytical expression of the bistatic SAR PT spectrum in constant-offset configuration. And the following imaging algorithm is based on the very expression.

First, making Taylor series expressions at=up to the second term, and we have:

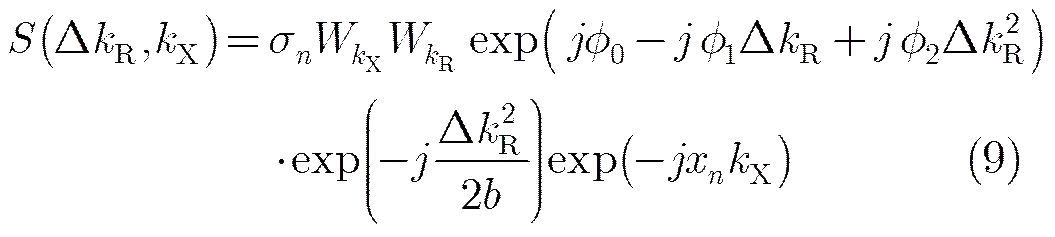
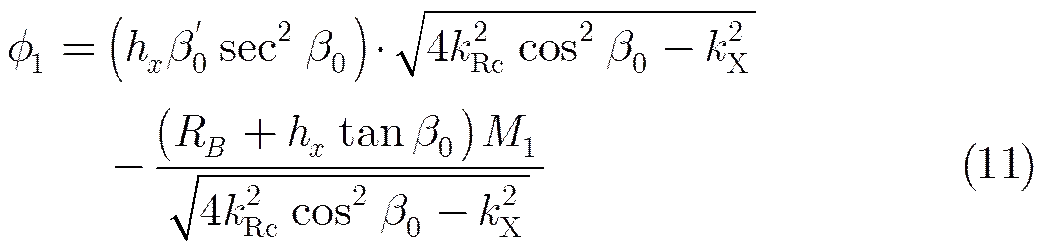
(12)

In the equations above, the expressions forMare given as

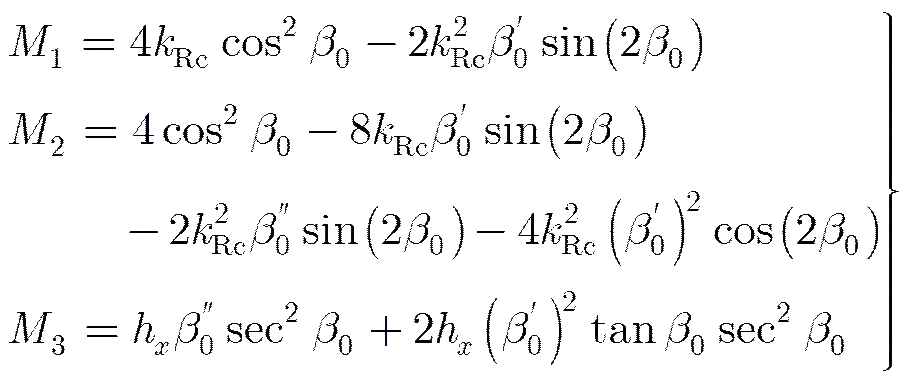
where

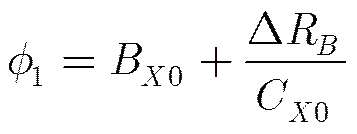
In the following, Eq. (15) is substituted into Eq. (9), and the signal arrives at:

To eliminate the range migration difference represented by, we adopt the SIFT imaging algorithm to the bistatic SAR signal processing. The matched-filter function is priority constructed as:

Performing the SIFT transform to the signal, we can get to:

Hereto, from Eq. (19) we can tell that, the processing consists of the following steps: the signal is multiplied by an exponential phase term with the formationfirstly, and then the convolution operation is carried out between the product obtained in the first step and another exponential term with the formation, in the end the result is multiplied by an exponential phase expressed by. Briefly speaking, the SIFT transform is realized by two times complex multiplications and one time convolution, and this is just in accordance with the monostatic case.

The signal after the SIFT transform is given as:

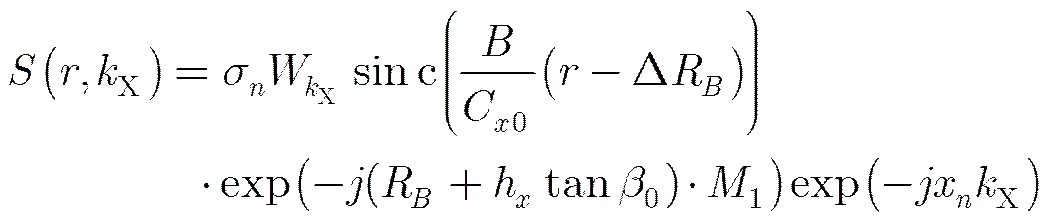
As can be seen, the range-dependence range migration has been eliminated properly,is no longer dependent on the Doppler parameters. After the imaging processing in range, the azimuth matched-filter function is constructed as

(21)

After azimuth compression, an Inverse FFT (IFFT) is performed to finish the whole imaging process to obtain the focused complex image. Note that, from Eq. (16), we can tell that, the parameters existed in the azimuth matched-filter function is range dependent. To realize satisfying focusing quality, this step needs to be operated line by line,.. dynamitic focusing. The block diagram of the proposed imaging algorithm is shown in Fig. 2.

4 Simulation Results

The simulation parameters for spaceborne bistatic SAR in constant-offset configuration is shown in Tab. 1. Nine targets are put in the imaging scene, the distance between any neighboring two targets is set to be 2000 m away from each other in range, and the distance between any two neighboring targets is set to be 1500 m away from each other in azimuth. The baseline is set to be 600 km from the transmitter to the receiver along the flight track, i.e. the length of the baseline is equal to the length of the closest distance from the flight track to the scene center, and this condition is the extreme situation in practice.

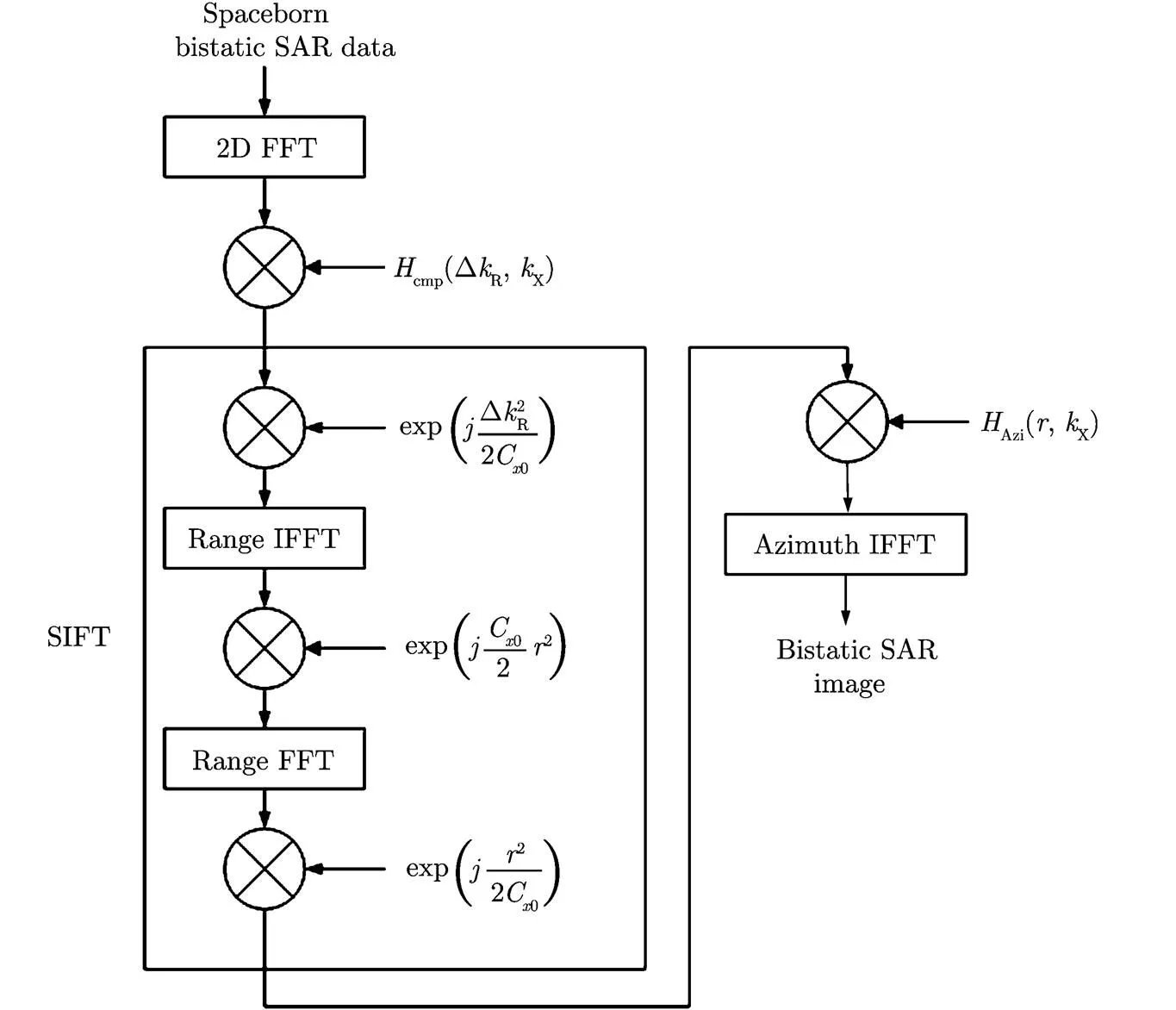
Fig. 2 Block diagram of the proposed SIFT imaging algorithm for spaceborne constant-offset bistatic SAR

The proposed SIFT imaging algorithm is carried out to equalize the difference of the range migration term, and the final imaging result is shown in Fig. 3. As can be seen, all the targets are quite well focused. The contour-plots and the impulse response functions both in the range and azimuth directions are shown in Fig. 4. The detailed values of the Impulse Response Width (IRW), the Peak Side-Lobe Ratio (PSLR) and the Integrated Side-Lobe Ratio (ISLR) are shown in Tab. 2. We can tell that both the reference target and the edge target in the imaging scene are well focused. To test the advantage of the proposed imaging algorithm, a comparable experiment is performed in accordance. The comparable imaging algorithm is performed based on Ref. [31], and corresponding imaging results for the reference and edge targets of the same imaging scene are given in Fig. 5. From the contour-plots and the impulse response function in both the range and azimuth direc- tions, we can find out that, the focusing quality for the reference range target is well enough. However, the focusing quality of the edge target is much worse than the proposed one, especially in the azimuth direction. Since the proposed SIFT imaging algorithm is carried out based on an exact analytical spectrum for constant- offset configuration, which can handle the bistatic SAR data with a very large length of the baseline. And the imaging algorithm carried out based on Ref. [31] is on the basis of an approximate spectrum whose spectrum precision is less than the proposed one, especially in the situation of large baseline situation, when the spectrum precision of Ref. [31] degrades dramatically.

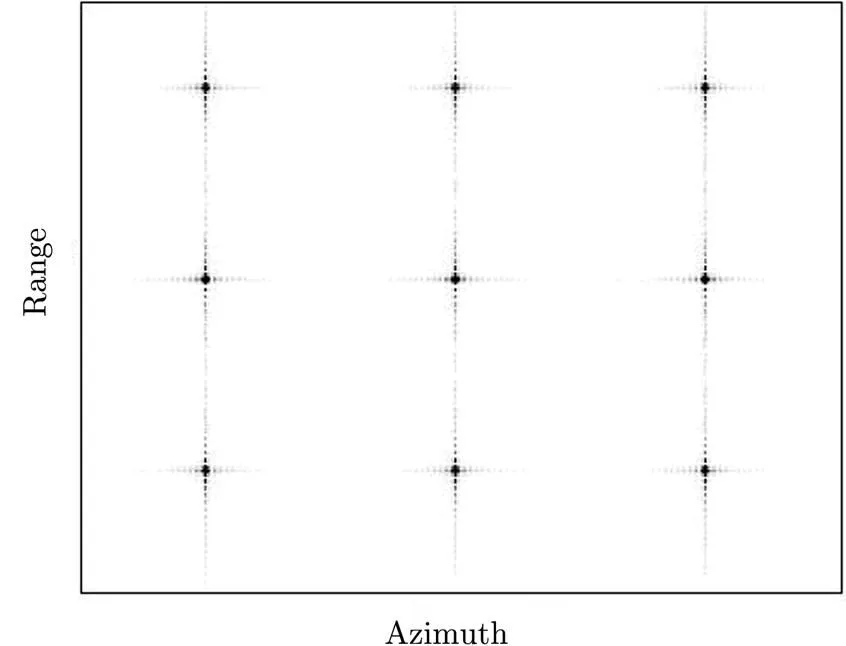
Fig. 3 Imaging results of the whole imaging scene

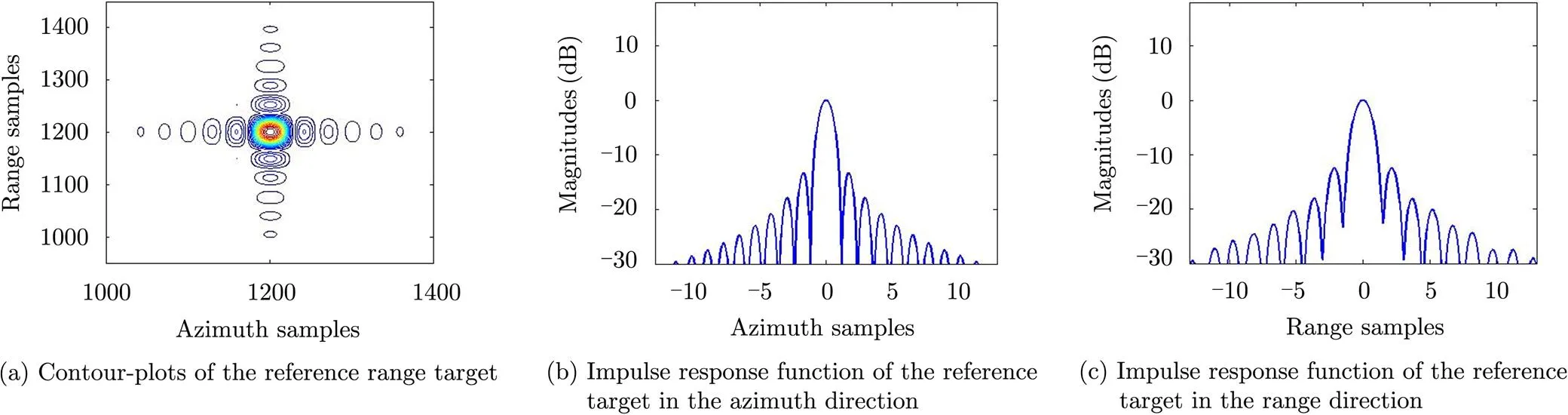
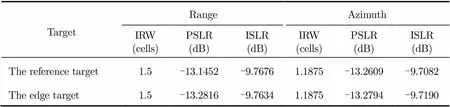
Tab. 2 Impulse response function analysis of the proposed algorithm

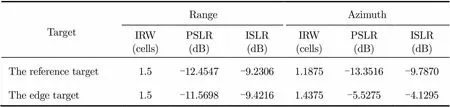
TargetRangeAzimuth IRW(cells)PSLR(dB)ISLR(dB)IRW(cells)PSLR(dB)ISLR(dB) The reference target1.5-12.4547-9.23061.1875-13.3516-9.7870 The edge target1.5-11.5698-9.42161.4375-5.5275-4.1295

5 Conclusion

The DSR term existed in the range history of bistatic SAR has been the most difficult obstacle to overcome in obtaining the precise bistatic SAR PT spectrum by using POSP for designing bistatic SAR imaging algorithms. The problem has been handled by the solution of a four-order equation with respect to the tangent of the half bistatic angle on the basis of the GBF method. The range migration problem for bistatic SAR imaging is solved by using the SIFT imaging algorithm based on an exact analytical bistatic PT spectrum presented in Ref. [27] in this article. And well-focused imaging results for the spaceborne constant-offset configuration are obtained.

Moreover, we have to note that, the proposed imaging algorithm is carried out based on an ideal geometry condition, which is hard to realize in practice. In real bistatic SAR systems, motion error is inevitable. The motion errors of bistatic SAR are even more complex than that of the monostatic SAR, and effective motion compensation algorithms deserve further studying cooperating with real bistatic SAR data.

[1] Duque S, Lopez-dekker P, and Mallorqui J. Single-pass bistatic SAR interferometry using fixed-receiver configurations: theory and experimental validation[J]., 2010, 48(6): 2740-2749.

[2] I Walterscheid, T Espeter, A Brenner,.. Bistatic SAR experiments with PAMIR and TerraSAR-X—setup, processing, and image results[J]., 2010, 48(8): 3268-3279.

[3] Rodriguez-Cassola M, Prats P, Schulze D,.. First bistatic spaceborne SAR experiments with TanDEM-X[J]., 2012, 9(1): 33-37.

[4] Prats P, Rodriguez-Cassola M, Marotti L,.. A versatile processing chain for experimental TanDEM-X product evaluation[C]. EUSAR, Aachen, Germany, June 2010: 4059-4062.

[5] Barber B. Theory of digital imaging from orbit synthetic aperture radar[J]., 1985, 6(6): 1009-1057.

[6] Ulander L, Hellsten H, and Stenstrom G. Synthetic-aperture radar processing using fast factorized back-projection[J]., 2003, 39(3): 760-776.

[7] Frolind P and Ulander L. Evaluation of angular interpolation kernels in fast back-projection SAR processing[J].-, 2006, 153(3): 243-249.

[8] Rodriguez-Cassola M, Prats P, and Krieger G. Efficient time-domain image formation with precise topography accommodation for general bistatic SAR configurations[J]., 2011, 47(4): 2949-2966.

[9] D’Aria D, Guarnieri A, and Rocca F. Focusing bistatic synthetic aperture radar using dip move out[J]., 2004, 42(7): 1362-1376.

[10] Loffeld O, Nies H, and Peters V. Models and useful relations for bistatic SAR processing[J]., 2004, 42(10): 2031-2038.

[11] Wang R, Loffeld O, Neo Y,.. Extending Loffeld's bistatic formula for the general bistatic SAR configuration[J].&, 2010, 4(1): 74-84.

[12] Chen Shi-chao, Wu Qi-song, Zhou Peng,.. A new look at Loffeld’s bistatic formula in tandem configuration[J]., 2012, 9(1): 710-714.

[13] Neo Y, Wong F, and Cumming I. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]., 2007, 4(1): 93-96.

[14] Neo Y, Wong F, and Cumming I. A comparison of point target spectra derived for bistatic SAR processing[J]., 2008, 46(9): 2481-2492.

[15] Clemente C and Soraghan J. Approximation of the bistatic slant range using Chebyshev polynomials[J]., 2012, 9(4): 682-686.

[16] Wang R, Deng Y, Loffeld O,.. Processing the azimuth- variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase[J]., 2011, 49(10): 3504-3520.

[17] Natroshvili K, Loffeld O, Nies H,.. Focusing of general bistatic SAR configuration data with 2-D inverse scaled FFT[J]., 2006, 44(10): 2718-2727.

[18] Nies H, Loffeld O, and Natroshvili K. Analysis and focusing of bistatic airborne SAR data[J]., 2007, 45(11): 3342-3349.

[19] Robert W, Loffeld O, Nies H,.. Chirp-scaling algorithm for bistatic SAR data in the constant-offset configuration[J]., 2009, 47(3): 952-963.

[20] Robert W, Loffeld O, Neo Y,.. Focusing bistatic SAR data in airborne/stationary configuration[J]., 2010, 48(1): 452-465.

[21] Zhong H and Liu X. An effective focusing approach for azimuth invariant bistatic SAR processing[J]., 2010, 90(1): 395-404.

[22] Neo Y, Wong F, and Cumming I. Focusing bistatic SAR data using nonlinear chirp scaling algorithm[J]., 2008, 46(9): 2493-2505.

[23] Neo Y, Wong F, and Cumming I. Processing of azimuth- invariant bistatic SAR data using the range-Doppler algorithm[J]., 2008, 46(1): 14-21.

[24] Zhang Zhen-hua, Xing Meng-dao, Ding Jin-shan,.. Focusing parallel bistatic SAR data using the analytic transfer function in the wavenumber domain[J]., 2007, 45(11): 3633-3645.

[25] Li Yan-ping, Zhang Zhen-hua, Xing Meng-dao,.. Bistatic spotlight SAR processing using the frequency-scaling algorithm[J]., 2008, 5(1): 48-52.

[26] Krieger G and Moreira A. Spaceborne bi- and multistatic SAR: potentials and challenges[J].-, 2006, 153(3): 184-198.

[27] Wu Qi-song, Liang Yi, Xing Meng-dao,.. Focusing of tandem bistatic-configuration data with range migration algorithm[J]., 2011, 8(1): 88-92.

[28] Liu Yue, Deng Yun-kai, and Robert Wang. Focus squint FMCW SAR data using inverse chirp-z transform based on an analytical point target reference spectrum[J]., 2012, 9(5): 866-870.

[29] Tang Yu and Xing Meng-dao. Two dimension chirp-Z transform for polar format imaging algorithm[C]. APSAR, Xi’an, China, November 2007: 743-746.

[30] Li Shen, Sun Jin-ping, Liu Zhen-hua,.. Research of chirp Z imaging algorithm for SAR[J]., 2008, 30(1): 48-51.

[31] Wu Yong-jun and Wu Xian-lian. Tandem bistatic squint SAR imaging algorithm based on the chirp-Z transform[J].&, 2010, 32(2): 383-387.

[32] Rigling B and Moses R. Motion measurement errors and autofocus in bistatic SAR[J]., 2006, 15(4): 1008-1016.

一种串行双基SAR的SIFT成像算法

陈士超 邢孟道 张双喜 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对串行双基地合成孔径雷达(SAR)中的距离徙动的空变问题，该文提出了一种变标逆傅里叶变换成像算法，通过两次相位相乘和一次卷积操作实现距离徙动的精确校正。该算法基于一种由几何关系公式方法推导出的严格解析双基点目标频谱，可以完成长基线距离比条件下的串行双基SAR的数据处理。仿真实验和对比实验验证了该算法的有效性和优越性。此外，不同于其他的变标算法，该变标逆傅里叶变换(SIFT)成像算法不依赖于信号的线性调频特性，同样适用于相位编码信号，有更广的适用范围。

双基地合成孔径雷达；2维点目标频谱；变标逆傅里叶变换

TN958

A

2095-283X(2013)01-0014-09

Chen Shi-chao.E-mail: chenshichao725@gmail.com.

CLC index: TN958

10.3724/SP.J.1300.2013.13018

Manuscript received March 11, 2013; revised March 15, 2013. Published online March 19, 2013.

Supported by the National Natural Science Foundation of China (No. 61222108, 60890072) and the National Research Program of China (“973” Program) (No. 2010CB731903).

Chen Shi-chao (1985-), was born in Heilongjiang, China. He received the B.S. degree in electrical engineering from Xidian University in 2009. He is currently working toward his Ph.D. degree in Signal Processing at National Lab for Radar Signal Processing of Xidian University. His major research interests are radar imaging and ground moving target indication (GMTI), especially bistatic synthetic aperture radar (BiSAR). E-mail: chenshichao725@gmail.com.

Xing Meng-dao (1975-), was born in Zhejiang, China. He received the Bachelor degree and the Ph.D. degree in 1997 and 2002, respectively, from Xidian University, both in electrical engineering. He is currently a full professor with the National Key Laboratory for Radar Signal Processing, Xidian University. His research interests include SAR, ISAR and over the horizon radar (OTHR).

Zhang Shuang-xi (1984-), was born in Fujian, China. He received the B.S. degree in technique of measuring control and instrument engineering from Xidian University in 2008. He is currently working toward Ph.D. degree in Signal Processing at National Key Lab of Radar Signal Processing of Xidian University. His major research interest is radar imaging (SAR).

Bao Zheng was born in Jiangsu, China. Currently, he is a professor with Xidian University and the chairman of the academic board of the National Key Lab of Radar signal Processing. He has authored or co-authored 6 books and published over 300 papers. Now, his research fields include space-time adaptive processing (STAP), radar imaging (SAR/ ISAR), automatic target recognition (ATR) and over-the-horizon radar (OTHR) signal processing. Professor Bao is a member of the Chinese Academy of Sciences.