两种典型网络中三种病毒传播模型的传播特性研究

朱鹏鹏 董建民

1阜阳师范学院 安徽 236000 2山东工业职业学院 山东 256414

0 引言

1998年，Watts和Strogatz提出了WS小世界模型，这种网络呈现出小世界的特性，度分布遵从泊松分布。

而大量的对现实复杂网络的统计结果表明，实际复杂网络的度分布服从Power Law分布。为了解释这种幂律分布，Barabasi和Albert在1999年提出了Scale-Free网络模型，即BA无标度网络模型。

在研究网络病毒传播之前，我们有必要先对传染病模型有所了解。生物学中早就开始对病毒传播进行了研究，并且建立了比较完善的流行病学传播的数学模型。

在典型的传播模型中，种群内的个体基本状态包括：S(Susceptible)——易染状态；I(Infected)——感染状态；R(Removed)——被移除状态(也称为免疫状态或恢复状态)。通常用这些状态之间的转换过程来命名不同的传染模型。例如，易染群体被感染，然后恢复健康并具有免疫性，称之为SIR模型。若易染群体被感染后，又返回到易染状态，则称之为SIS模型。下面针对生物学中SI模型、SIS模型、SIR模型具体介绍病毒的传播过程。

1 SI模型的传播特性

在 SI 模型中，每个个体处于两种状态中的一种：易感染状态(Susceptible)和已感染状态(Infective)。模型中每个个体的状态变迁过程是：易感染状态—>已感染状态。

取节点数N=1000，感染率因子为β=0.02，分别在相同平均度为10的BA网络和小世界网络中任选一个节点作为被感染的节点，仿真结果如图1所示，横坐标为传播时间，纵坐标为整个网络中节点被感染的百分比。从图中可以看到，病毒经过一个较长时间的初始感染阶段，当被感染节点积累到一定的数量以后，进入快速感染阶段，当绝大多数网络节点都被感染以后，进入饱和阶段。仿真发现，在病毒传播的早期，病毒在BA网络中的传播更快，显然BA网络中连接分布的不均匀性有利于病毒的快速传播。

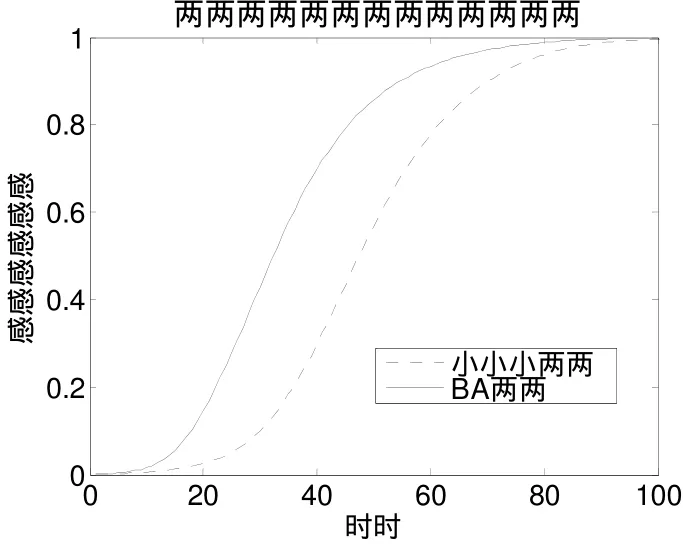
图1 SI模型中病毒的传播趋势

2 SIS模型的传播特性

在SIS模型中，每个个体也只有两种状态：易感染状态与已感染状态，但与SI模型不同的是，它考虑了个体感染后被治愈的可能，被治愈的个体对该病毒仍然是易感染的。

病人每天被治愈的总数的比例为δ，称为日治愈率，即该模型考虑了病人可以治愈为健康者的实际情况。

取节点数N=1000，感染率因子为β=0.02，治愈率为δ=0.08，分别在相同平均度为10的BA网络和小世界网络中任选一个节点作为被感染的节点，仿真结果如图2所示，横坐标为传播时间，纵坐标为整个网络被感染的百分比。从仿真结果可知，在初始感染节点数目相同的情况下，BA网络中病毒的传播到达稳态时的感染密度比均匀网络(小世界网络)中的要大。

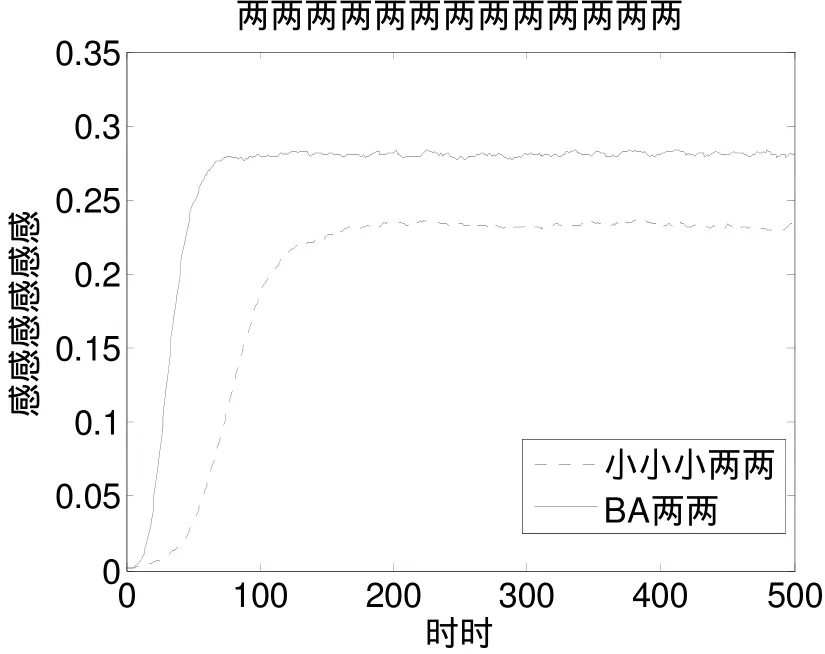
图2 SIS 模型中病毒的传播趋势

3 SIR模型的传播特性

另外一类被广泛研究的病毒传播模型是SIR模型，它描述的传播行为是，被染个体要么被治愈后获得对该病毒的免疫能力，要么成为死亡个体从系统中移除。在单位时间内，易感染病毒的个体以β平均速率接触所有网络中其他状态的体，又以平均速率δ治愈成正常或死亡状态。

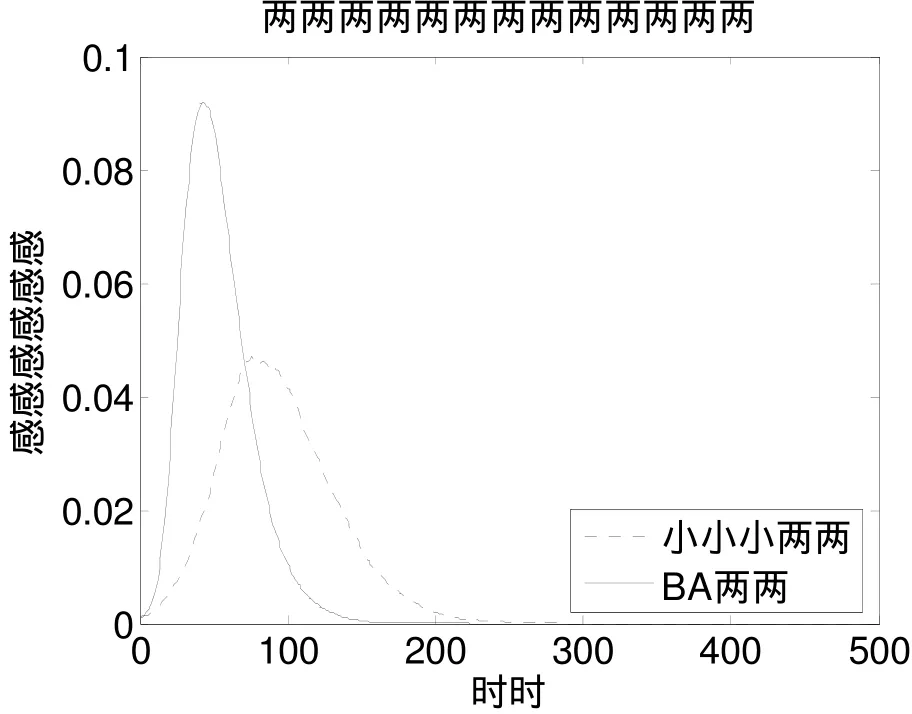
图3 SIR模型中病毒的传播趋势

对于SIR模型来讲，当被感染节点治愈成为健康的节点以后，相当于把此节点从整个网络中除去，网络节点总数由N变为 N-1。图3中给出了SIR模型中病毒传播的趋势。取节点数N=1000，感染率因子为β=0.02，治愈率为δ=0.08。分别在相同平均度为10的BA网络和小世界网络中任选一个节点作为被感染的节点，横坐标为传播时间，纵坐标为感染节点数。可以看到，随着时间的增加，最后两种网络感染节点数都变为0，但BA网络被感染节点的峰值高于小世界网络，病毒在BA网络的流行和消亡都快于小世界网络。

4 结束语

近年来，复杂网络研究吸引了大批来自不同学科学者们的注意，使得复杂网络领域获得较快发展。同样，作为复杂网络理论的重要组成部分的传播行为也引起了学者们的广泛关注。目前国际国内对复杂网络中病毒传播模型的研究都集中于讨论静态网络中的传播行为，研究各种网络拓扑结构和性质对病毒传播的影响，在该领域已有许多重要发现，但是复杂网络传播理论还不完善，还有很多问题有待解决。

[1]D.J.Watts.Small Words: The dynamic of Networks between Order and Randomness[M].Princeton : Princeton University Press.1999.

[2]A.-L.Barabasi.Linked: The New Science of Networks[M].Cambridge: Perseus.2002.

[3]N T J Bailey.The Mathematical Theory of Infectious Diseases and its Applications[M].New York: Hafner Press.1975.

[4]R M Anderson,R M May.Infectious diseases in humans[M].Oxford: Oxford University Press.1992.

[5]O.Diekmann,J A P.Heesterbeek.Mathematical Epidemiology of Infectious Disease: Model Building,Analysis and Interpretation[M].John Wiley & Son publisher.2000.

[6]G.Streftaris,G J.Gibson.Statistical Inference for Stochastic Epidemic Models[J].Proceedings of the 17th international Workshop on Statistical Modelling,China.2002.

[7]Y.Wang,C X.Wang.Modeling the Effects of Timing Parameters on Virus Propagation[J].Washington DC,October.27.2003.

[8]J C.Frauenthal.Mathematical Modeling in Epidemiology[J].New York: Spring-Verlag.1980.12