商业银行信用风险评估实证分析及方法比较

李君艺 张宇华

1东莞职业技术学院计算机工程系 广东 523808 2广东工业大学计算机学院 广东 510006

0 引言

我国的金融风险主要表现为信用风险，我国商业银行信用风险管理已由传统经验判断时期逐步发展到现代信用风险模型化阶段。随着管理信息系统的广泛使用和电子商务的深入发展，我国商业银行大都拥有大量客户数据，而面对海量数据，传统的信用风险管理方法逐渐无法负荷。数据挖掘技术的出现，为解决海量数据下的信用风险管理问题提供了新的思路和方法。数据挖掘是以人工智能为基础的数据分析技术，是从大量的、不完全的、有噪声、模糊的、随机的数据中，提炼隐含其中的、具有潜在作用的信息和知识的过程。数据挖掘可以为商业银行信用风险提供诸多分析方法，本文对三种常用的数据挖掘方法——多元判别分析、聚类分析和贝叶斯网络模型进行实证研究，通过结果分析，比较三者作为信用风险评估方法的优劣。

1 商业银行信用风险评估指标

信用风险评估方法的验证数据选用某商业银行的数据，选择已成功申请房贷的 6000条个人客户数据为研究对象，其中5000条数据作为训练样本，1000条数据作为结果验证。LEVEL表示信用风险等级，划分为 High(H)、Middle(M)、Low(L)三个等级，各等级在样本数据中大致均匀分布。LEVEL作为响应变量或目标变量，其余的变量为客户信用指标集，反应客户的各项属性，即特征属性变量，如表1所示。

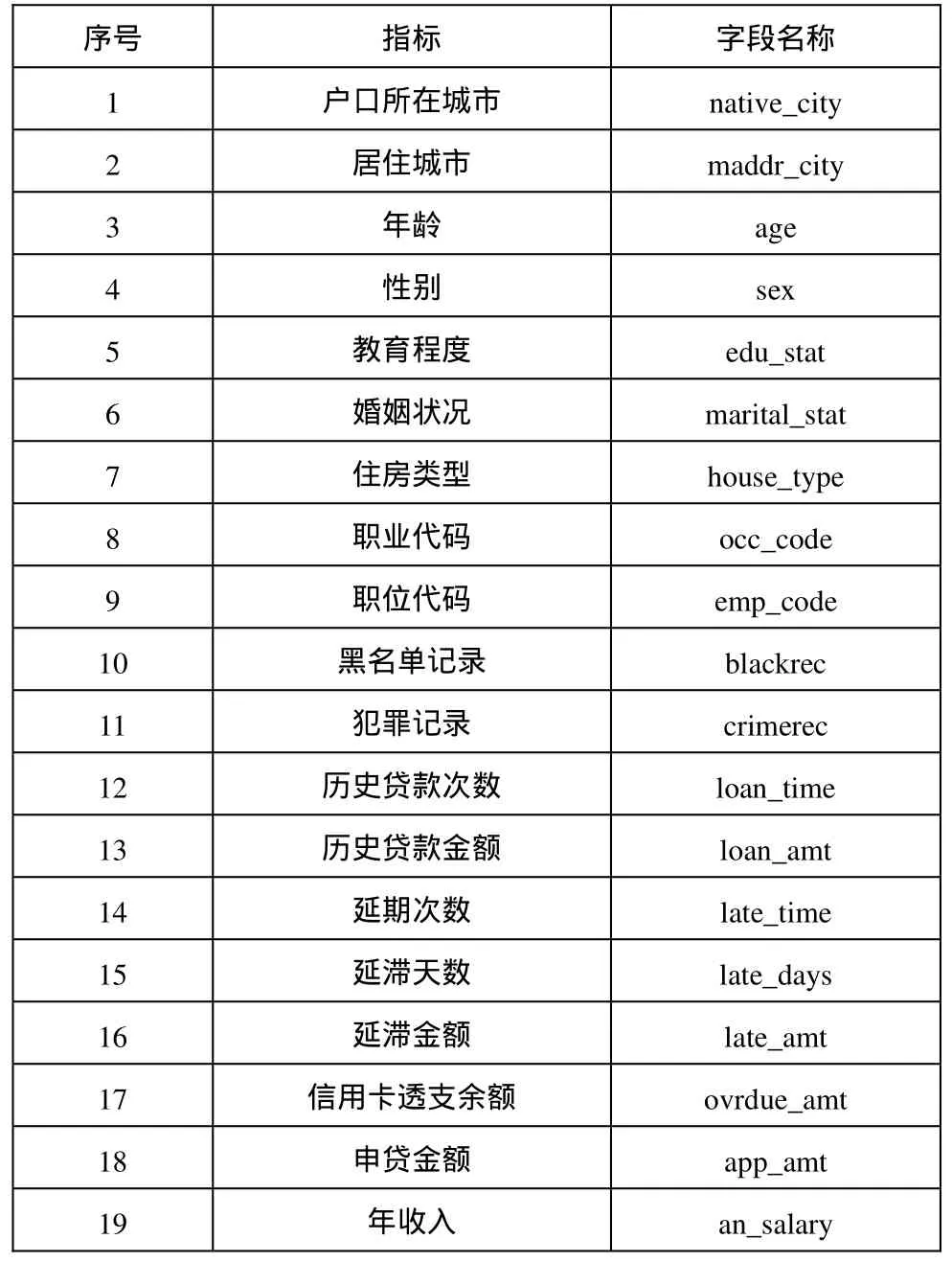
表1 属性指标列表

以上数据以SAS数据集的形式储存于ODS数据层，训练数据统一存放于数据集studydata，验证数据存放于数据集newdata。

信用风险评估方法的实现功能是：在给定的风险等级分类体系下，根据分析客户的以上特征属性变量，自动确定客户的信用风险等级类别LEVEL。我们将通过对三种不同的分析方法进行验证，比较三种方法在信用风险评估分析中的性能及准确度。

2 实证分析

2.1 多元判别分析

判别分析是根据表明研究对象特征的变量值判别样品所属类型的一种分类方法。根据样本的已知分类及所测得的数据，筛选出最能表明研究对象特征的变量，并根据这些变量和已知类别，建立使误判率最小的判别函数。在风险评估算法中，可把风险等级作为分类变量，各个指标属性作为数值变量，从已知分类数据中训练出判别函数，用于客户风险等级的分类预测。

我们利用SAS系统软件中的STEPDISC、DISCRIM过程对信用风险评估指标进行判别分析。过程如下：

(1)指标筛选

首先，利用STEPDISC过程对指标进行筛选，选出对判别分析结果相关性较大的指标。proc stepdisc data=studydata method=sw;class X20;var X1-X19;run;

STEPDISC过程逐步选出F值最大，即对判别效果贡献最大的变量，选入模型，最后选出Pr>F小于判据0.15的变量。结果在19个变量中选择了X3，X5，X10，X14，X18，X19共6个变量。

(2)判别分析过程

评估指标的变量既有离散型变量也有连续型变量，数据的分布不能确定，我们须采用SAS中的DISCRIM过程。下面我们将以 studydata作为训练样本，在前面已经过STEPDISC的变量筛选，现在我们基于 studydata对新样本newdata进行风险等级分类。

proc discrim data=newdata testdata=studydata testout=result list;

class x20;

var x3 x5 x10 x14 x18 x19;

run;

Studydata中的风险等级分类共有H、M、L三级，即X20有三种取值。运行过程是首先得出三个级别的线性判别函数的系数和常数项，用回代法将newdata每个观测的变量代入三个判别函数，哪个函数值大，观测就属于哪一类。这里我们使用了 LIST选项，使分类结果自动列出，并显视各观测分到每一类的后验概率，最后结果是观测被分到后验概率最大的那一项(图1)。

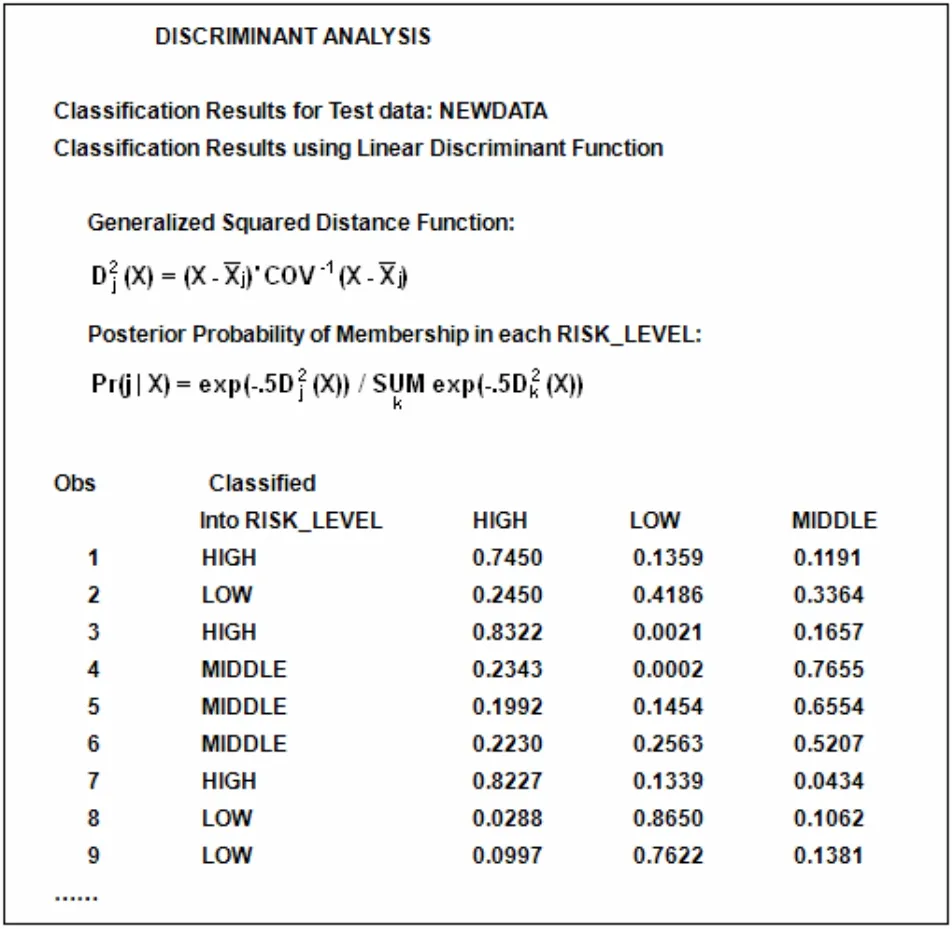
图1 PROC DISCRIM部分运行结果

我们把DISCRIM过程的分类结果与银行内部的实际风险评级结果相比，分类正确的数据为776条，准确率达到77%以上。然后我们尝试把studydata样本提高为8000条数据时，newdata的分类准确率提升为80.6%。

2.2 聚类分析

聚类分析和判别分析有相似的作用，都是起到分类的作用。但是，判别分析是已知分类然后总结出判别规则，是一种有指导的学习；而聚类分析则是有了一批样本，不知道它们的分类，甚至连分成几类也不知道，希望用某种方法把观测进行合理的分类，使得同一类的观测比较接近，不同类的观测相差较多，这是无指导的学习。因聚类分析适合于分析样本量少的数据，下面我们只从newdata中选取100条数据作分析。

SAS中的聚类分析过程有 11种分类方法(METHOD)，下面我们采用最短距离法(METHOD=SINGLE)，即通过计算两类观测间最近一对的距离，得出分类结果。

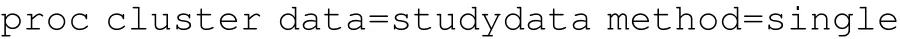
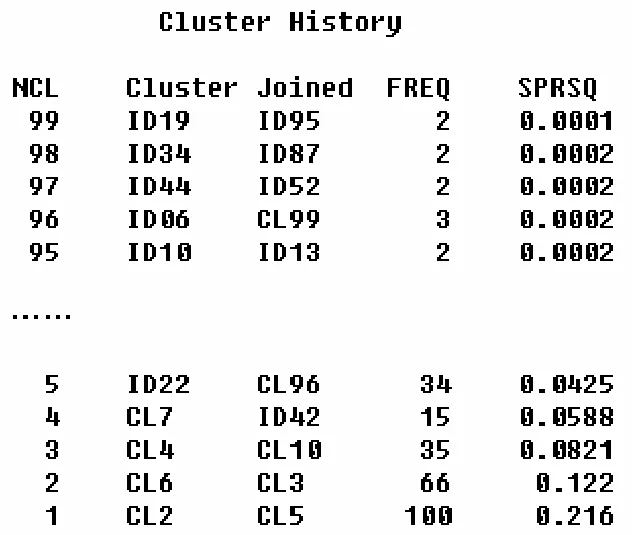
图2 PROC CLUSTER运行结果

如图2所示，Cluster History中的变量依次表示分类的类数、原分类、每步合并入的类、此步类中的观测数、R平方。系统聚类法首先将所有样本观测各独自视为1类，然后逐步合并至只有1类。然后，我们设信用等级分类数ncl为3，接下来，可以用proc tree和proc means进一步完善后续工作。

最后，根据数据集result可以得到将100个客户分为3类，再结合对各类客户的定性评分，可以把信用风险定为高，中，低三个级别。与实际评级结果相比，运算结果准确的条数达 74条，准确率为 74%。聚类分析只能应用于数据量较少的样本，并且只能对样本进行分类，无法具体确定每一类的风险级别。确定每个分类的风险级别需要结合因子分析或人为定性分析。

2.3 贝叶斯网络模型

贝叶斯网络的构建可以通过学习和人工构建两种方式进行。人工构建通过专家经验手工构造，学习则是通过数据分析获得，即利用机器学习的方法分析数据来获得贝叶斯网络。在训练样本充分的情况下，可以从数据中训练出贝叶斯网络模型。贝叶斯网络模型的构建过程包括网络结构学习和参数学习，步骤如下：

(1)各个指标作为节点，运用K2算法对studydata样本进行训练，寻找CH评分高的贝叶斯网络模型，确定节点间的关系，生成贝叶斯网络结构表。

(2)利用最大似然估计算法进行参数学习，确定节点的概率分配，为每个节点各生成一个条件概率表。

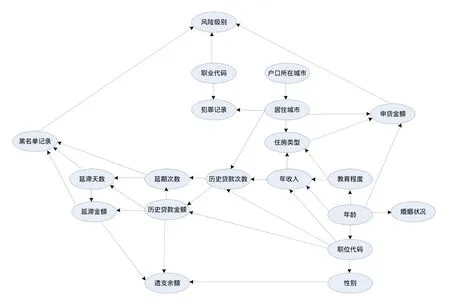
图3 信用风险评估贝叶斯网络模型

通过以上步骤构建的贝叶斯网络模型结构如图3所示。现对模型进行验证。把从前面参数学习取得的 20个条件概率表，建立20个数据集，依次命名为T1,T2,…,T20。把网络结构表建立一个独立的数据集，命名为 network。SAS算法将对客户数据(newdata)逐条处理，过程如下：

(1)读取客户数据，初始化运算公式：

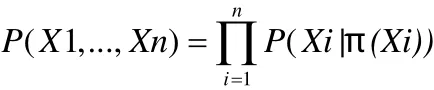
(2)搜索表Network，获取属性变量Xi(i=1,2,…,19)的父节点；

(3)搜索表Ti(i=1,2,…,19)，获得该子节点与父节点的联合条件概率，将其加入运算公式；

(4)搜索表 T20，把 3个风险等级下的条件概率分别加入运算公式，得出客户在3个风险等级(H,M,L)的概率结果，最后确定把客户分到概率最高的一个等级。

验证过程是通过输入客户的数据(newdata)，得出客户在3个信用风险级别(H,M,L)的概率，最后确定客户属于概率最大的一个级别。算法流程见图4。

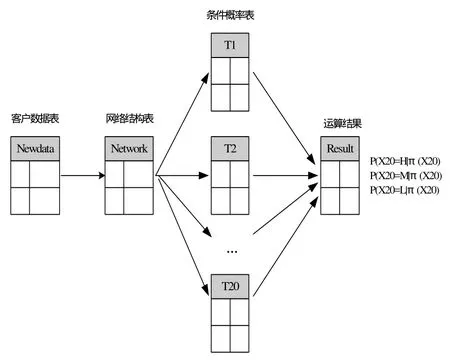
图4 贝叶斯网络验证算法流程图

根据以上过程，我们使用newdata样本的1000条数据进行结果验证。把模型的分类结果与银行内部的实际风险评级结果相比，分类正确的数据为886条，准确率达到88.6%。

3 结论

从表2的结果看，三种分析方法相比，对于中、低风险级别的客户数据，贝叶斯网络方法的准确率优于判别分析和聚类分析；对于高风险级别的客户数据，贝叶斯网络的准确率与其它两种方法基本持平。贝叶斯网络模型在判断高风险客户上没有明显的优势，大约是因为高风险客户的指标属性集近似吻合条件独立的假定。但是，对于中、低风险的客户而言，其影响还款能力的各方面因素大多是相关的，贝叶斯网络模型在解决条件依赖方面有明显优势。总体来看，贝叶斯网络模型的总体准确率高于判别分析和聚类分析。贝叶斯网络能运用所有的属性指标并明确确定每个指标的依赖关系和条件概率，判别分析则只选取相关性较高的指标进行概率估算，因此贝叶斯网络的精确度显然要高于判别分析；与聚类分析相比，贝叶斯网络是基于对大量历史数据进行学习而获得的，并能用于分析数据规模较大的样本，而聚类分析能应用于数据量较少的样本，并且只能对样本进行分类，无法具体确定每一类的风险级别，在这一点上，贝叶斯网络模型明显优于聚类分析。

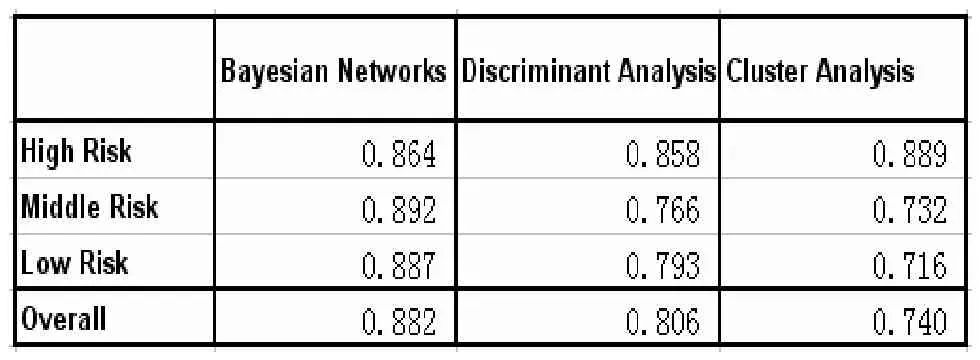
表2 三种方法正确率对照表

[1]张连文,郭海鹏.贝叶斯网引论[M].科学出版社.2006.

[2]谭浩强.SAS/PC统计分析软件使用技术[M].国防工业出版社.1996.

[3]李君艺,梁智城.SAS判别分析在商业银行信用风险评估中的应用[J].计算机安全.2011.

[4]薄纯林，王宗军.基于贝叶斯网络的商业银行操作风险管理[J].金融理论与实践.2008.

[5]汪办兴.我国商业银行信用风险模型的国际比较与改进.当代经济科学[J].2007.

[6]Jiawei Han,Micheline Kamber.数据挖掘概念与技术[M].机械工业出版社.2008.

[7]General J.Financial analysis using Bayesian networks[J].Applied Sochastic Modelsin Bussiness and Industry.2001.17(1):57-67.