基于混沌序列的压缩感知测量矩阵构造算法

林 斌，彭玉楼

长沙理工大学 计算机与通信工程学院，长沙 410114

基于混沌序列的压缩感知测量矩阵构造算法

林 斌，彭玉楼

长沙理工大学 计算机与通信工程学院，长沙 410114

1 引言

近年来，Donoho和Cande[1-2]等人提出了一种新型采样理论，基于稀疏表示的压缩感知（Compressed Sensing，CS），突破了传统乃奎斯特采样理论对采样频率的限制，实现了对数据获取的同时进行适当地压缩，克服了原始采样数据量较大、采样时间较长，计算机后续处理以及数据存储空间等物理资源浪费严重的问题。

在CS理论中，有三个核心问题[3]：一是信号稀疏变换；二是测量矩阵设计；三是重构算法构造。其中测量矩阵设计的好坏将直接影响后续重建信号的误差的大小。目前广泛使用的测量矩阵可以分为确定性和随机性测量矩阵。

当前国内外有学者提出将混沌序列应用到CS的测量矩阵之中，Nguyen Linh-Trung等人在文献[4]中利用混沌序列构造出满足高斯分布的测量矩阵，实验结果表明该测量矩阵具有一般随机测量矩阵的性质，甚至稍胜于一般随机测量矩阵；Lei Yu在文献[5]中利用混沌序列构造一测量矩阵，证明该矩阵满足RIP性质，同时也验证该矩阵的可行性；顾国生等人在文献[6]中提出了一种通过基于符号混沌系统有限型子转移生成的伪随机序列构造压缩感知观测矩阵，同时验证该测量矩阵的可行性和有效性，但其算法复杂度较高，计算时间较长。

由于Bernoulli测量矩阵是随机矩阵，每次实验产生的矩阵都不相同，所以稳定性较差。本文利用混沌序列良好的随机性质，针对Bernoulli随机序列在稳定性方面的不足进行研究，提出一种复杂度较低的测量矩阵构造算法。该算法在混沌序列的基础上通过符号函数映射成具有Bernoulli分布的随机序列，利用此随机序列构造测量矩阵。实验仿真证明，与其他类型的随机测量矩阵进行比较，基于Logistic混沌—贝努利测量矩阵是可行有效的。

2 压缩感知理论

设 X∈RN×1为一维信号，信号 X在一组N×N维正交基Ψ={Ψ1Ψ2…ΨN}上展开为：

其中，θk=＜X，Ψk＞，X和θ均为 N×1维向量。当信号 X在某个正交基Ψ上仅有K＜＜N个非零系数θk时，称Ψ为信号X的稀疏基，θ是K-稀疏的。现实中的信号往往不是稀疏的，需要经过式（1）的转换，故该步骤称为信号的稀疏化。常用的稀疏基Ψ有：正余弦基、小波基、Chirplet基及Curvelet基等。

将信号XN×1投影到一组测量矩阵ΦM×N（其中M＜＜N）上，得到X的M个采样数据YM×1，即

结合式（1）和式（2），可以得到采集数据Y与变换系数θ之间的关系为：

压缩感知数据采集示意图为如图1所示。

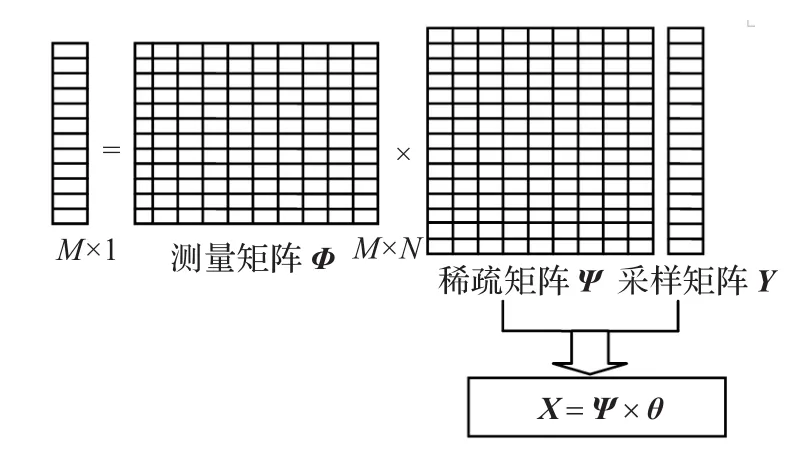
图1 压缩感知数据采集示意图

为了能从式（3）中准确重构出原始信号，测量矩阵Φ和正交变换基Ψ不相关[7-8]。文献[7]指出Φ必须满足（Restricted Isometry Property，RIP）准则，即对任意具有严格K-稀疏的矢量v，Φ满足：

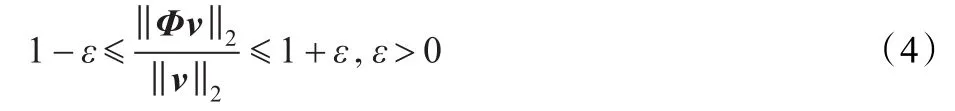
常用的测量矩阵有，随机高斯矩阵、Bernoulli矩阵、傅里叶矩阵等与常用的正交变换基不相关，很大程度上满足RIP性质[9-10]。

在满足以上条件下，可以利用l0范数优化方法求解θ的精确解或者是一个逼近，即通过式（5）求解[1，7]：

由于式（5）的优化问题是一个NP-hard问题，所以可用l1范数代替l0范数[11]：

关于重构算法，早期学者提出了正交匹配追踪（OMP）[8]、匹配追综（MP）[12]、梯度投影法（GP）[13]等。近年来也有学者不断提出新的重构算法，比如修正自适应匹配追踪（MAMP）[14]算法，迭代硬阈值重构算法（IIHT）[15]算法等。

3 基于Logistic混沌—贝努利测量矩阵构造算法

混沌是非线性系统所独有且广泛存在的一种非周期运动形式，由于混沌系统产生的序列具有确定性和随机性的统一、规律性以及遍历性等良好的伪随机性质，所以在非线性控制、信号处理、保密通信等领域有着广泛应用。以下是本文利用混沌序列性质构造测量矩阵的算法。

已知Logistic混沌系统如式（7）所示：

该Logistic系统在参数 μ∈[1.872，2.0]区间的条件下，当初值x0=0.23，0.37，或0.7时，其Lyapunov指数均大于0，此时的Logistic系统是混沌系统[16]。

文献[17]提出当μ=2.0时，由该Logistic系统产生的序列满足Bernoulli分布，同时也满足RIP性质，则由Logistic系统产生的序列可作为CS的测量矩阵。

本文构造测量矩阵算法步骤为：

步骤1经过反复的实验对比，发现在 μ=2.0情况下，初值x0=0.23，0.37，或0.7时，重构误差MSE分别为0.097 95，0.082 61和 0.089 51，取值之间有略微差异。故本文取μ=2.0，x0=0.37，通过该Logistic混沌系统来产生混沌序列，其中序列长度n=M×N-1。

步骤2将步骤1生成的混沌序列通过式子（8）符号函数映射成序列。

步骤3将步骤3生成的序列取 N长截断形成M×N维测量矩阵Φ。

文献[5]中的算法复杂度要比O(N2)大，而本文算法复杂度为O(M×N)(M＜＜N)。图2是Bernoulli随机序列和Chaos-Bernoulli序列的对比图以及它们之间的直方图对比图。

图2 Bernoulli随机序列和Chaos-Bernoulli序列的对比图及直方图对比图

由图2可以看出，与Bernoulli序列相比，Chaos-Bernoulli序列具有更好的平均性及稳定性，其随机序列中－1，1的个数比趋于1∶1。

4 实验结果

根据以上步骤构造出基于Logistic的Chaos-Bernoulli的测量矩阵，本文对一维信号和二维图像信号进行仿真实验，验证该测量矩阵的可行性与有效性，并与Gaussian随机矩阵和Bernoulli随机矩阵进行对比。

4.1 一维信号仿真实验

本文选取长度为N=256的一维信号，测量数M=0.5×N，压缩比为：。重构算法选取文献[7]的OMP算法。实验结果如图3所示。

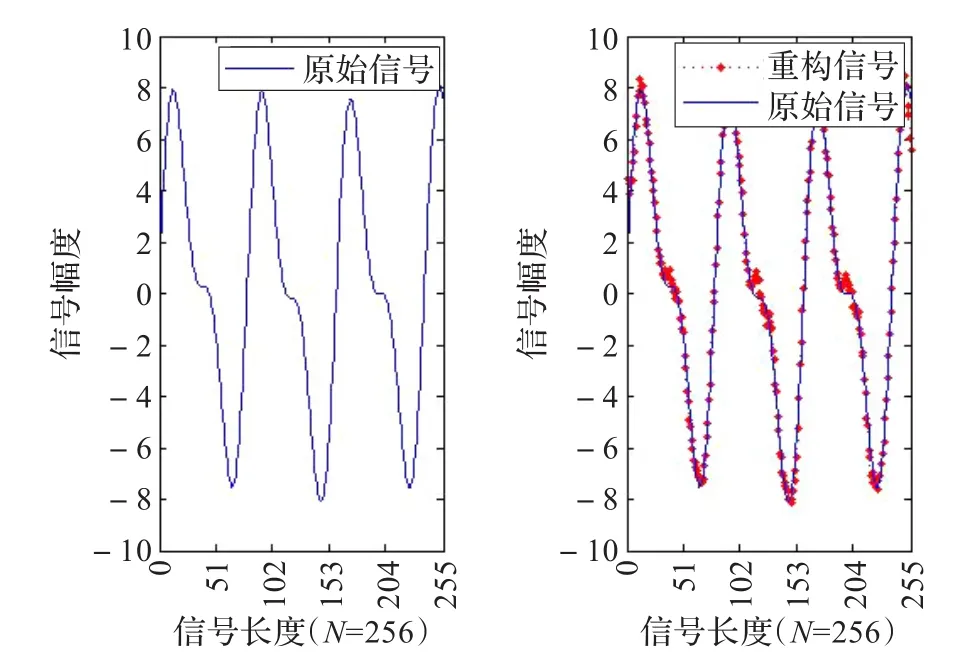
图3 一维信号Chaos-Bernoulli测量矩阵重构实验图

图3可以看出Chaos-Bernoulli测量矩阵几乎可以完全重构原始信号。在信号长度N=256，测量数M=128的条件下，表1列出了各测量矩阵在峰值信噪比（PSNR）、重构误差（MSE）和匹配度α各个数据方面的对比。由于随机测量矩阵每次实验产生的矩阵都不相同，所以取20次实验结果取平均值作为表1的结果。其中，当 X为原始信号，Xˉ为重建信号时，峰值信噪比（PSNR）、重构误差（MSE）和匹配度α的计算方法为：

表1 信号长度N=256，测量数M=128，各矩阵性能比较

从表1可以看出，Chaos-Bernoulli测量矩阵相对于其他测量矩阵来说，PSNR值有1～3 dB的提高，MSE、α有一定程度的提高。在不同的压缩比的情况下，图4给出了重构信号PSNR的对比图。

图4 一维信号在不同测量矩阵下的峰值信噪比随压缩比变化图

由图4可以看出，本文算法在不同压缩比的条件下，Chaos-Bernoulli测量矩阵与其他测量矩阵相比具有较好的稳定性，峰值信噪比均优于其他测量矩阵。

4.2 二维图像仿真实验

本文采用Lena、Cameraman和Barbara256×256图像在不同压缩比下进行仿真实验，重构算法采用OMP算法。

首先，选取Lena图像，在压缩比M/N=0.5情况下讨论不同测量矩阵对重构效果的影响，实验结果如图5。

图5 各测量矩阵Lena图像重构效果对比（M/N=0.5）

图5直观地给出各个测量矩阵在同一压缩比的情况下对二维图像的重构效果。其中Chaos-Bernoulli矩阵的重构效果要优于其他测量矩阵。为了进一步说明图5的实验结果，图6给出各个图像在不同测量矩阵下的峰值信噪比随压缩比的变化图。同理，由于其他用于对比的测量矩阵是随机矩阵，因此取20次实验选取平均值作为实验数据。其中I是原图像是重构图像，W和H分别是图像的宽度和高度，二维图像的PSNR计算方法为：

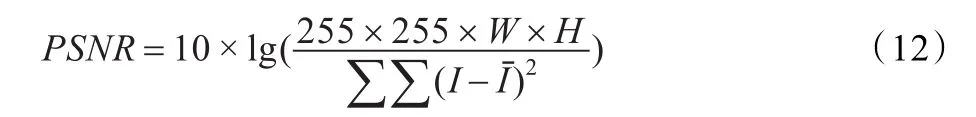
从图6可以看到，本文提出测量矩阵重构算法在重构后的图像PSNR方面均优于Gaussian、Bernoulli随机测量矩阵，且在压缩比越大的情况下效果越明显。

图6 各个图像在不同测量矩阵下的峰值信噪比随压缩比变化图

5 结束语

本文针对Bernoulli测量矩阵在稳定性方面的不足，利用混沌系统特征提出一种Logistic Chaos-Bernoulli测量矩阵构造算法。对一维二维信号的重构效果进行数值仿真，仿真结果表明，与Bernoulli测量矩阵相比，本文提出的测量矩阵重构效果良好，重构信号PSNR值平均有1～3 dB的提高，并与Gaussian随机测量矩阵相比，PSNR在压缩比越大的情况下效果越明显，具有一定的实用价值，今后将在基于超混沌的测量矩阵构造算法作进一步的研究。

[1]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory，2006，52（4）：1289-1306.

[2]Candes E.Compressive sampling[C]//Proceedings of the International Congress of Mathematicians，Madrid，Spain，2006.

[3]石光明，刘丹华.压缩感知理论及研究进展[J].电子学报，2009，37（5）：1070-1081.

[4]Linh-Trung N，Van Phong D，Hussain Z M，et al.Compressed sensing using chaos filters[C]//Telecommunication Networks and Applications Conference，2008.

[5]Yu L，Barbot J P，Zheng G，et al.Compressive sensing with chaotic sequence[J].IEEE Signal Processing Letters，2010，17（8）：731-734.

[6]顾国生，战荫伟.一种混沌序列在压缩感知观测矩阵构造中的应用[C]//第十五届全国图像图形学学术会议，2010：111-114.

[7]Candes E，Romberg J，Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52（4）：489-509.

[8]Tropp J，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

[9]Donoho D，Tsaig Y.Extensions of compressed sensing signal processing[J].Signal Processing，2006，86（3）：533-548.

[10]Candes E.Compressive sampling[C]//Congress of Mathematic，2006，3：1433-1452.

[11]Baraniuk R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine，2007，24（4）：118-121.

[12]Trop J A.Greed is good：algorithmic results for sparse approximation[J].IEEE Transactions on Information Theory，2004，50（10）：2231-2242.

[13]Figueiredo M A T，Nowak R D，Wright S J.Gradient projection for sparse reconstruction：application to compressed sensing and other inverse problem[J].Journal of Selected Topics in Signal Processing：Special Issue on Convex Optimization Methods for Signal Processing，2007，1（4）：586-598.

[14]甘伟，许录平.一种自适应压缩感知重构算法[J].系统工程与电子技术，2011，33（9）：1948-1953.

[15]张宗念，李金徽，黄仁泰.迭代硬阈值压缩感知重构算法——IIHT[J].计算机应用，2011，31（8）：2123-2125.

[16]林卫强，黄元石.Logistic混沌序列的随机性分析[J].福州大学学报：自然科学版，2004，32（3）：270-274.

[17]凌聪，孙松庚.Logistic映射扩频序列的相关分布[J].电子学报，1999，27（1）：140-141.

LIN Bin,PENG Yulou

College of Computer&Communication Engineering,Changsha University of Science and Technology,Changsha 410114,China

The measurement matrix construction algorithm is one of important research direction in compressed sensing.A measurement matrix algorithm based on Logistic Chaos-Bernoulli sequence is proposed according to the pseudo-random property of chaos sequence.It uses the one-dimensional Logistic chaotic system to generate the chaotic sequence,the pseudo-random sequence with Bernoulli distribution is generated by the symbol function and the sequence is used to construct the measurement matrix. Simulation results show that,the proposed algorithm performs better than the Bernoulli random measurement matrix and the PSNR of construct signal is improved about 1～3 dB,and it is feasible and effective by numerical analysis after comparing with other types of measure matrix.

compressed sensing;measurement matrix;chaotic system;Bernoulli distribution

测量矩阵的构造算法是压缩感知中重要的研究方向之一。提出一种基于Logistic混沌—贝努利序列（Chaos-Bernoulli）测量矩阵构造算法，该算法利用了混沌序列良好的伪随机性质，通过一维Logistic混沌系统产生混沌序列，再通过符号函数生成具有贝努利分布的伪随机序列从而构造出压缩感知测量矩阵。实验仿真结果表明，该算法优于贝努利随机测量矩阵，信号重构的峰值信噪比PSNR有1～3 dB的提高，并与其他类型的测量矩阵进行比较，数值分析结果证明该算法是可行有效的。

压缩感知；测量矩阵；混沌系统；贝努利分布

A

TN911.7

10.3778/j.issn.1002-8331.1202-0344

LIN Bin,PENG Yulou.Measurement matrix construction algorithm for compressed sensing based on chaos sequence. Computer Engineering and Applications,2013,49（23）：199-202.

林斌（1987—），男，硕士研究生，主要研究方向：压缩感知、图像处理；彭玉楼（1968—），男，博士，副教授，主要研究方向：小波理论、图像处理、压缩感知。E-mail：linbin1987@163.com

2012-02-20

2012-04-18

1002-8331（2013）23-0199-04

CNKI出版日期：2012-06-15 http://www.cnki.net/kcms/detail/11.2127.TP.20120615.1726.021.html