食品安全评价指标设定方法研究
鄂旭,王彬,侯建,沈德海,冯冠
(1.渤海大学食品科学研究院,辽宁锦州 121001;2.渤海大学信息科学与技术学院,辽宁锦州 121001;3.北京交通大学中国产业安全研究中心,北京 100044)
近年来,国内外不断发生“疯牛病”、“三鹿奶粉”等重大食品安全问题,严重影响了人民的身心健康,同时也充分暴露出食品安全管理体系的薄弱。食品安全问题非常复杂,它涉及从“农田”到“餐桌”的整个过程,是一个涉及多个领域、多个环节的动态问题。食品安全既受到系统内部因素的影响,如食品卫生政策、食品生产条件、食品科技水平等,又受到系统外部因素的影响,如自然灾害、环境污染等。这些因素的影响程度,需要准确测度出来,并且需要对这些因素之间的关联程度进行准确衡量。为此,国内外学者对食品安全评价问题进行了深入的研究。目前,国内外大多数食品安全指标体系的内容是围绕导致食品不安全的主要因素来进行设计的,主要包括两个方面的内容:一个是食品中微生物污染程度,另一个是食品中有害物质含量。当前对食品安全评价的主流方法有相对评价和绝对评价相结合、排序评价和分类评价相结合、动态评价和静态评价相结合三种方法,但这些方法都需要食品安全评价的先验知识做基础,有待进一步提高[1-2]。
粗糙集理论为此提供了有效的处理技术和方法。由于它无需提供所处理数据之外的任何先验信息,因此在智能信息处理研究中发挥着越来越重要的作用[3-5]。粗糙集(Rough Sets)理论是由波兰数学家Pawlak 于1982 年首先提出,它提供了一套严格处理知识发现中基本分类问题的数学方法,是一种刻画模糊地、不完整性和不确定性的数学工具[6-8]。
本文基于粗糙集理论提出了一种食品安全评价指标精简算法。
1 粗糙集基础知识
粗粗糙集及其在应用中所涉及的一些基本概念如下[3-6]。
定义1:一个信息系统被定义为一个四元组

其中,U={x1,x2,…,xn}是一组对象的有限集合,U称为论域;A 是属性的有限集合,它又可分为不相交的两个集合:条件属性集C 和决策属性集D,即A=C∪D,且C∩D=Ø;V 是一组属性值的集合,V=Ua∈AVa,Va是属性a 的值域;f 为信息函数,有f(x,a)∈Va,任意a∈A,任意x∈U。
令X⊆U,且R 为一等价关系。当X 为某些R 基本范畴的并时,我们称X 是R 可定义的,否则X 为R不可定义的。R 可定义集是论域的子集,它可在知识库K 中被精确的定义,而R 不可定义集不能在这个知识库中被定义。R 可定义集称为R 精确集,而R 不可定义集称为非精确集或R 粗集。
定义2:假设给定的知识库K=(U,R),对于每个子集X∈U 和一个等价格关系R∈Ind(K),可以根据R 的基本集合的描述来划分集合X。为了衡量{des(Yi),Yi∈R}精确的说明X 中对象的隶属度情况,考虑两个子集:
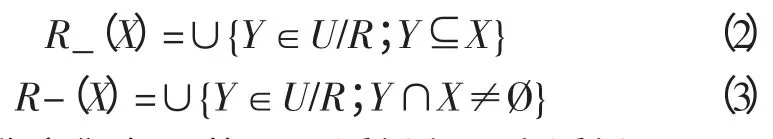
分别称它们为X 的R 下近似和R 上近似。
上近似和下近似也可以用下面的等式表达:
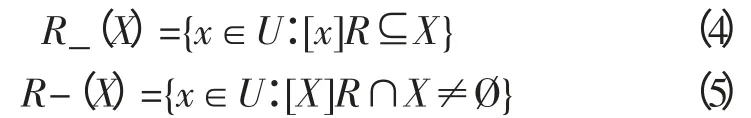
posR(X)=R_(X)称为X 的R 正域,把negR(X)=UR_(X)称为X 的R 负域,把bnR(X)称为X 的边界域。正域是粗糙集理论中一个相当重要的概念,在以后属性和属性值的约简中都要用到。用图例描述一个二维近似空间中集合X 的上近似、下近似概念。这个空间是由划分成基本区域的长方块构成的(U,R)定义,每个基本区域代表R 的一个等价类,阴影区域代表X 的边界,是X 的不可确定区域,除R_(X)以外所有的区域是负域。
定义3:信息系统S=(U,A,V,f),设P⊆A 而且x,y∈U,称x,y 关于P 是不可分辨的,如果满足:f(x,a)=f(y,a),Va∈P,由属性P 产生的不可分辨关系定义为:Ind(P)={(x,y)∈U×U f(x,a)=f(y,a)任意a∈P}不可分辨关系也称等价关系,它将U 划分为若干个等价类,记为U/Ind(P)。
定义4:若Q⊆P 是独立的,并且ind(Q)=ind(P),则称Q 是关系族集P 的一个约简。在P 中所有不可省的关系集合称为P 的核,记为core(P)。也就是说P 的核等于P 中所有约简的交集,即:core(P)=∩red(P)。
定义5:设系统S=(U,A,V,f),其中A=C∪D,a(x)是x 在属性a 上的值,分辨矩阵M 为:
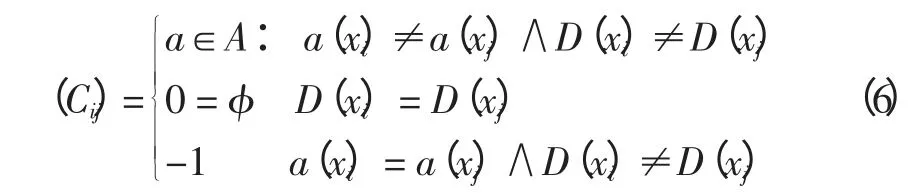
同时分辨矩阵中的核就是组合数为1 的属性。
定义6:属性的重要性 在分辨矩阵M=(Cij)N×N中,相应的属性重要性计算公式为:
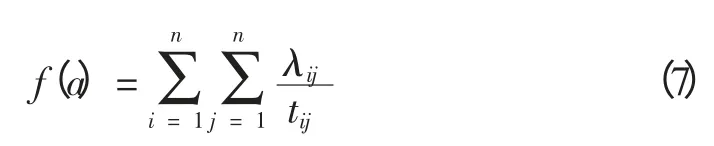
2 算法描述与实现
2.1 算法描述
输入:决策表(U,A∪{d}),其中A=∪ai,i=1,…,n。
输出:约简集reduct。
步骤:
1)令约简后得到的属性集合等于条件属性集合,即reduct=R;
2)计算可辨识矩阵M,并找出所有不包含核属性的属性组合S;
3)将所有不包含核属性的属性组合表示析取范式的形式,即
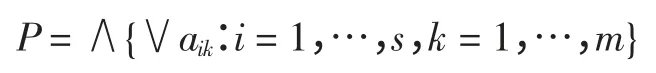
4)将P 转化为析取范式的形式,并按照公式(2)计算属性的重要性。
5)选择其中重要性最小的属性a,使得reduct-re duct-{a};
6)判断约简操作是否成立,若成立,删除因条件属性约简而引入的冗余样本和不相容样本,i=i+1,转(5);否则恢复约简该属性前的样本数据,结束约简。
第(6)步中的判断条件为p1/p0<α。式中p0为执行本次约简操作前知识表中样本的数量,p1为执行约简后引入的不相容样本数。α 为阈值,根据实际需要确定,取=5%。
2.2 算法实现
利用系统默认生成的窗体作为主窗体(Dm_Main-Form.cs),并为其添加一个MenuStrip(主菜单)控件和一个StatusStrip(状态栏)控件,各个控件布局如图1所示。
数据分析窗口如图2 所示。

图1 系统主界面Fig.1 Main interface of system
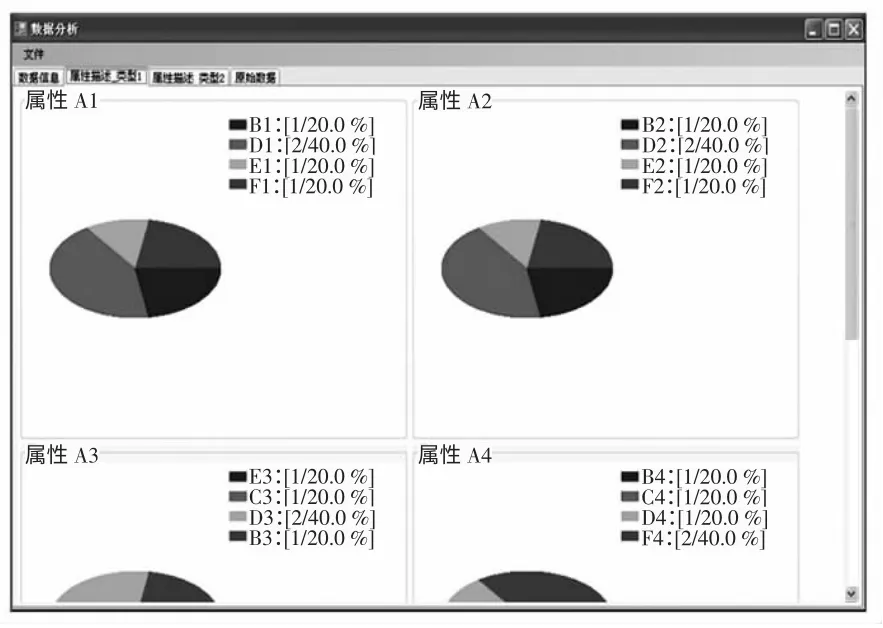
图2 数据分析界面Fig.2 Data analysis interface
3 结论
本文针对食品安全评价指标的选定与精简问题进行了研究,利用可分辨矩阵和和正域概念提出了一种精简食品安全评价指标的新方法。该方法不但能够准确选定食品安全评价指标,而且能够在保持原有信息系统分类能力不变的情况下精简食品安全评价指标,发现数据中蕴涵的知识模式。但本算法也存在算法时间复杂度较高等缺点,有待于以后进一步研究。
[1]邓聪文,朱雪冬,王俊能.食品安全评价及其方法简述[J].畜禽业,2009,19(12):8-10
[2]鄂旭,韩芳,侯建,等.面向食品安全评价的属性约简方法研究[J].吉林大学学报,2013,31(3):1-6
[3]Pawlak Z.Rough Sets and Fuzzy Sets[J].Fuzzy Sets and Systems,1985,17:99-102
[4]Krysikiewicz M.Rough Set Approach to Incomplete Information System[J].Information Sciences,1998,112:39-49
[5]王国胤.Rough 集理论与知识获取[M].西安:西安交通大学出版社,2005
[6]张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2006
[7]曾黄麟.粗糙集理论及其应用[M].重庆:重庆大学出版社,1996
[8]E Xu,Yang Yuqiang,Ren Yongchang.A new method of attribute reduction based on information quantity in an incomplete system[J].Journal of software,2012,7(8):1881-1888

