四点接触球转盘轴承中几何参数对摩擦力矩的影响

陆静，洪荣晶，陈捷，高学海,2

(1．南京工业大学 机械与动力工程学院，南京 210009；2.上海欧际柯特回转支承有限公司，上海 201906)

单排四点接触球转盘轴承是一种内圈或外圈带有传动齿的特大型轴承，可以和驱动小齿轮啮合传动扭矩，在风力发电机组中一般用于偏航系统、变桨系统中。该轴承由于不易拆装且拆装费用高，其寿命要求与机组寿命相同，一般在20年以上[1]。而轴承摩擦力矩不仅影响能量的损失，也会引起轴承运转过程中温度的上升，使润滑剂劣化、磨损加剧甚至引起轴承的损坏[2]。因此计算轴承的摩擦力矩及分析其影响因素对四点接触球转盘轴承的设计、制造、使用和维护具有重要意义。

文献[3]给出了风电轴承摩擦力矩的计算方法；FAG，IMO，Kaydon，Rollix，Rothe Erde[4-8]在产品样本中也给出了风电轴承摩擦力矩的计算模型。这些都是经验公式，只与轴承承受的外加载荷有关，无法分析轴承几何参数对摩擦力矩的影响。文献[9]利用有限元方法通过得出变桨轴承空载时球与内、外沟道的接触载荷来计算轴承的摩擦力矩，同时计算了单排球与双排球的力矩比，并与实测结果进行了对比。文献[10]对四点接触球转盘轴承与交叉滚子转盘轴承在轴向力作用下滚动体与滚道之间的摩擦力矩进行了对比分析。

下文通过理论计算求出四点接触球转盘轴承接触载荷的分布，进而计算钢球与沟道之间的摩擦力矩，同时分析初始接触角、沟曲率半径系数、钢球直径、游隙对钢球与沟道之间摩擦力矩的影响(讨论轴承几何参数对摩擦力矩的影响时不考虑加工精度因素的影响)。

1 摩擦力矩

1.1 摩擦的来源

转盘轴承中的摩擦主要来源于以下几个方面[2]：(1)材料弹性滞后引起的纯滚动摩擦；(2)滚动接触面上的差动滑动引起的摩擦；(3)钢球沿接触面中心法线的自旋滑动引起的摩擦；(4)滑动接触部位的纯滑动摩擦(在保持架结构的转盘轴承中，纯滑动摩擦包括保持架与引导挡边的摩擦以及球与保持架兜孔的摩擦；在隔离块结构的转盘轴承中，纯滑动摩擦为球与隔离块的摩擦)；(5)润滑剂的黏性摩擦。

在上述产生摩擦的5个方面中，钢球与沟道之间的摩擦包括材料弹性滞后引起的摩擦、滚动接触面上的差动滑动引起的摩擦和钢球自旋滑动引起的摩擦[10]。对于滑动接触部位的纯滑动摩擦，这些接触面之间的作用力都难以计算，其间的滑动摩擦尚无完整的分析方法; 而润滑剂的黏性阻力包括润滑剂的绕流阻力和搅拌阻力，受轴承填脂量和脂黏度的影响，很难精确计算[11]。文献[12]认为中重载荷下的球轴承摩擦产生的主要原因是钢球与沟道接触变形区内的滑动。故在此只讨论钢球与沟道之间的摩擦力矩。

1.2 摩擦力矩的计算

设四点接触球转盘轴承在轴向力作用下全部钢球与内、外沟道接触时同时存在弹性滞后摩擦力矩、差动滑动摩擦力矩和自旋滑动摩擦力矩[10]。

在轴向力、径向力、倾覆力矩的综合作用下，钢球在滚动过程中受到的弹性滞后摩擦力矩Mh、差动滑动摩擦力矩Md、自旋滑动摩擦力矩Ms分别为[11，13-14]

cosαedj)+Qeujbeuj(Dpw+Dwcosαeuj)] ，

(1)

(2)

L(e)iujsinαiuj+QedjaedjL(e)edjsinαedj+Qeujaeuj·

L(e)eujsinαeuj] ，

(3)

式中：ah为弹性滞后系数，取0.007；Dpw为球组节圆直径；Dw为钢球直径；α为钢球与沟道的实际接触角；Z为钢球数；Q为钢球与沟道接触处的法向载荷；μ为滑动摩擦因数，取0.07；fi，fe分别为内、外圈沟曲率半径系数；a,b为钢球与沟道接触椭圆的长、短半轴；L(e)为第二类完全椭圆积分；下标j表示钢球标号；i表示内圈；e表示外圈；d表示沟道下半部分；u表示沟道上半部分。

钢球与沟道之间的摩擦力矩Mb为

Mb=Mh+Md+Ms。

(4)

2 几何参数对摩擦力矩的影响

以013.40.1600四点接触球转盘轴承为例，采用文中的计算模型对钢球与沟道之间的摩擦力矩进行计算分析。013.40.1600轴承的结构参数为:Dw=40 mm，Z=114，初始接触角α0=45°(4个接触角相等)，Dpw=1 600 mm，fi=fe=0.52。该轴承采用隔离块结构的保持架；轴承承受的轴向力为240 kN，径向力为60 kN，倾覆力矩为360 kN·m。该轴承的载荷及位置关系如图1所示。在图1b所示的坐标系中，坐标系原点O在转盘轴承中心处，y轴平行于倾覆力矩方向，xz平面平行于倾覆平面，φ为接触位置与x轴的夹角，φ=0时为钢球标号j=1时的位置。Cid表示内圈下半沟道的曲率中心，Ceu表示外圈上半沟道的曲率中心，Ciu表示内圈上半沟道的曲率中心，Ced表示外圈下半沟道的曲率中心。

2.1 α0对摩擦力矩的影响

图2为受载情况以及其他参数不变时，初始接触角分别为40°,45°,50°,55°,60°时，轴承摩擦力矩的变化图。由图2可知，球与沟道间的摩擦力矩随初始接触角的增大而减小；弹性滞后摩擦力矩、差动滑动摩擦力矩以及自旋滑动摩擦力矩也都随着初始接触角的增大而减小，其中差动滑动摩擦力矩、自旋滑动摩擦力矩减小的幅度较大，而弹性滞后摩擦力矩减小的幅度较小。

图1 转盘轴承的载荷及位置关系图

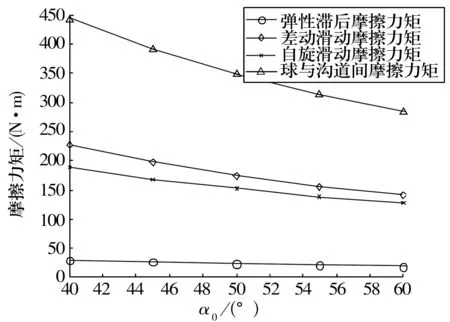
图2 初始接触角α0对摩擦力矩的影响

随初始接触角增大，轴承摩擦力矩减小的主要原因是球与沟道之间的接触载荷发生了变化。图3为不同初始接触角下轴承的接触载荷，当初始接触角从40°到60°逐渐增大时，在CidCeu接触方向上，发生接触的钢球数没有变化，但大部分接触钢球与沟道间的接触载荷明显减小；在CiuCed接触方向上，发生接触的钢球数减少，同时球与沟道接触时的接触载荷也减小。因此弹性滞后摩擦力矩、差动滑动摩擦力矩、自旋滑动摩擦力矩都减小，从而球与沟道之间的摩擦力矩也减小。

图3 α0对接触载荷的影响

2.2 fi(e)对摩擦力矩的影响

图4为其他参数及受力状况不变时，摩擦力矩随沟曲率半径系数的变化图。由图4可知，当沟曲率半径系数由0.51增大到0.54，弹性滞后摩擦力矩逐渐增大，但增大的幅度很小，几乎不变；自旋滑动摩擦力矩逐渐减小，变化幅度较大；差动滑动摩擦力矩减小的幅度非常大；球与沟道间摩擦力矩逐渐减小，且幅度较大。

图4 沟曲率半径系数fi(e)对摩擦力矩的影响

随着沟曲率半径系数的增大，弹性滞后摩擦力矩增大的主要原因是球与沟道之间的接触载荷发生了变化。图5为不同沟曲率半径系数下轴承的接触载荷。如图5所示，在CidCeu接触方向上发生接触的钢球数没有变化，大部分球的接触载荷增大；在CiuCed接触方向上发生接触的钢球数增加，且大部分钢球的接触载荷增大，因此弹性滞后摩擦力矩增大。

差动滑动摩擦力矩、自旋滑动摩擦力矩减小的主要原因是接触椭圆长半轴变短。图6为沟曲率半径系数对接触椭圆长半轴的影响。如图6所示，大部分钢球与沟道间的接触椭圆的长半轴随沟曲率半径系数的增大而变短，而且长半轴变短的幅度要远远大于接触载荷增大的幅度，因此差动滑动摩擦力矩、自旋滑动摩擦力矩都减小。从(2)～(3)式可知，差动滑动摩擦力矩减小的幅度大于自旋滑动摩擦力矩减小的幅度。

图5 沟曲率半径系数fi(e)对接触载荷的影响

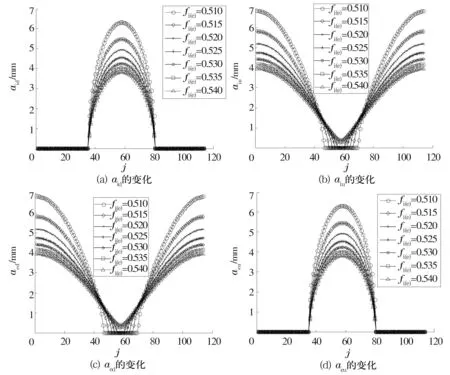
图6 沟曲率半径系数fi(e)对接触椭圆长半轴的影响

2.3 Dw对摩擦力矩的影响

四点接触球转盘轴承在装配时，装入的球直径增大或减小时，装入的球的数量也会产生相应的变化，但轴承回转中心不变。当钢球直径分别选取30,35,40,45,50,55,60 mm时，对应的钢球数分别为152,130,114,101,91,83,76。图7为轴承的受力情况及其他参数不变时，钢球直径对摩擦力矩的影响。由图7可知，当钢球直径逐渐增大时，球与沟道之间的摩擦力矩变化幅度很小；弹性滞后摩擦力矩与差动滑动摩擦力矩逐渐减小，差动滑动摩擦力矩减小的幅度较大；自旋滑动摩擦力矩逐渐增大，且增大的幅度较大。

图8为钢球直径对钢球和沟道间的接触载荷的影响。由图8可知，随着钢球直径增大,钢球数目减少，发生接触的钢球数减少，钢球与沟道间的接触载荷明显增大。图9为钢球直径对接触椭圆长半轴的影响。由图9可知，随着钢球直径的增大，钢球数目减少，球与沟道接触时的接触椭圆长半轴明显增大，因此由(3)式可知自旋滑动摩擦力矩也逐渐增大，而且增大的幅度较大。虽然接触载荷、接触椭圆长半轴增大，但是从(2)式可知，钢球直径直接影响差动滑动摩擦力矩的大小，因此差动滑动摩擦力矩随钢球直径的增大而减小，并且减小的幅度较大。

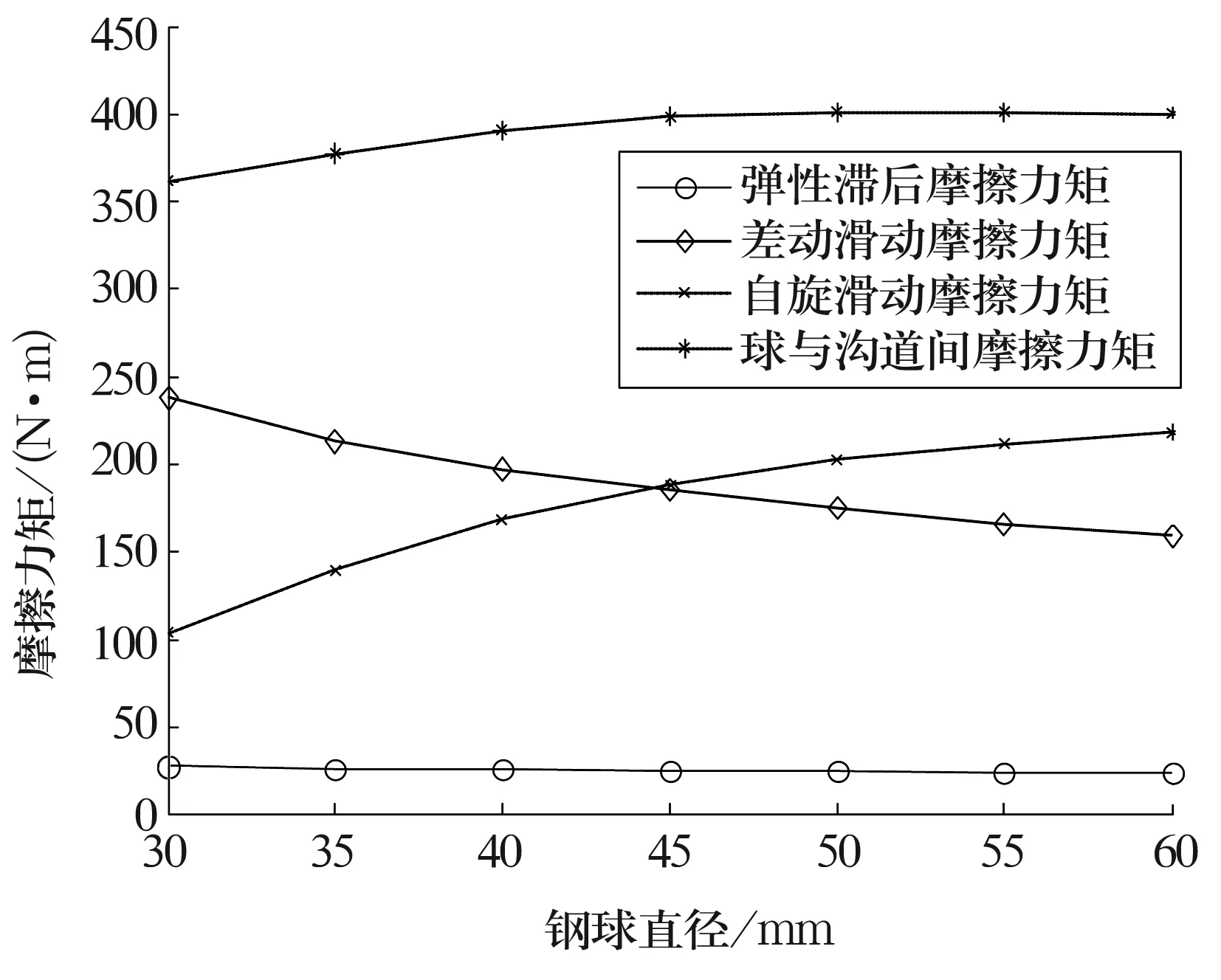
图7 钢球直径Dw对摩擦力矩的影响

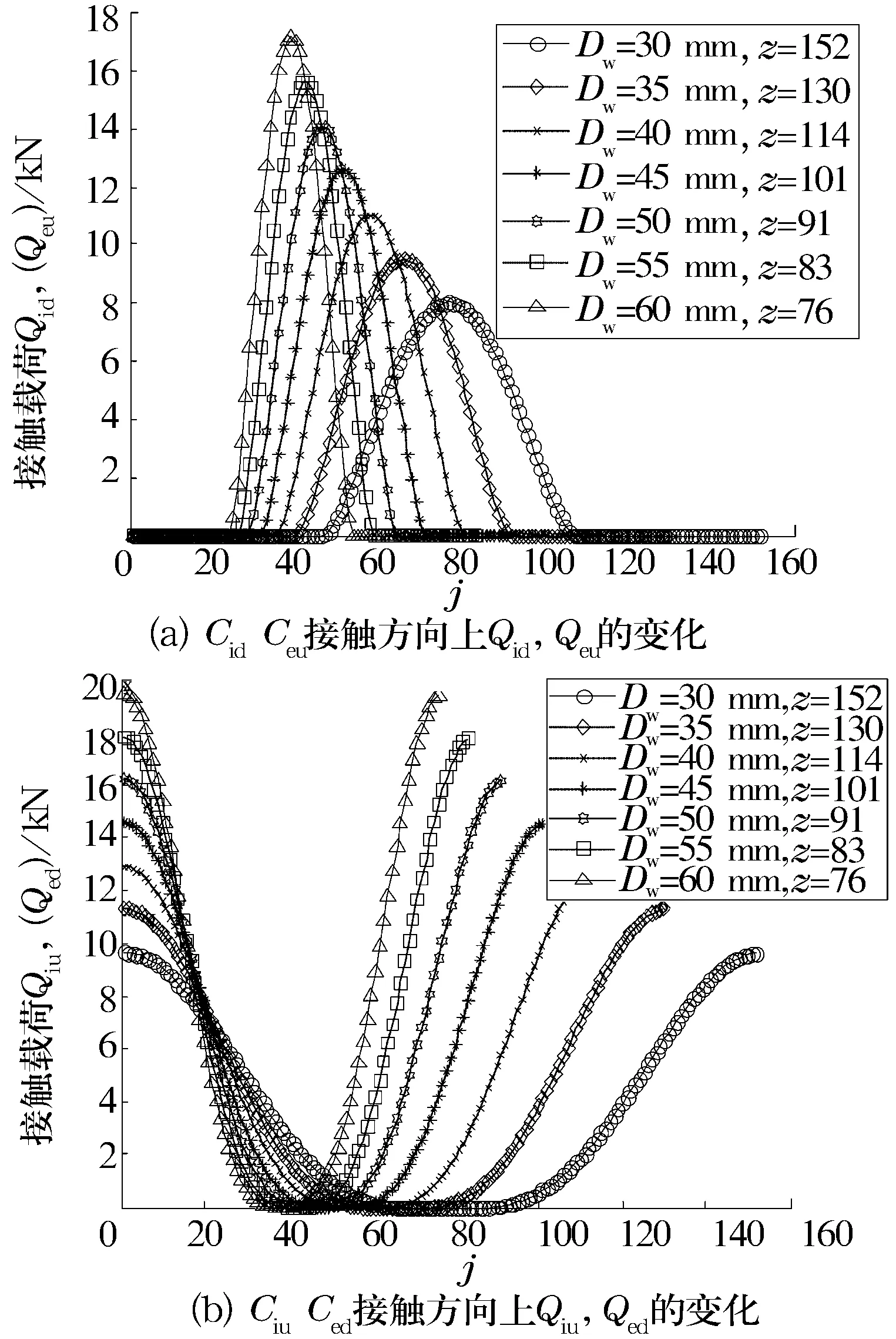
图8 钢球直径Dw对接触载荷的影响

2.4 游隙对摩擦力矩的影响

图10为轴承受力情况及其他参数不变时，不同游隙(-0.05，-0.03，-0.01，0，0.01，0.03，0.05 mm)下轴承的摩擦力矩。由图10可知，当游隙从-0.05～-0.01 mm逐渐增大时，钢球与沟道间的摩擦力矩、差动滑动摩擦力矩以及自旋滑动摩擦力矩都急剧减小，弹性滞后摩擦力矩也逐渐减小，但变化幅度较小；当游隙从-0.01～0.05 mm逐渐增大时，摩擦力矩没有明显变化。

当游隙从-0.05～-0.01mm逐渐增大时，摩擦力矩急剧减小的主要原因是钢球与沟道之间的接触载荷发生了变化。如图11所示，当游隙为-0.05，-0.03 mm时，所有钢球与内、外圈的上、下沟道都发生接触，且接触载荷很大；当游隙为-0.01 mm时，只有部分钢球与沟道发生接触，且相应的接触载荷要小很多，所以摩擦力矩急剧减小。当游隙从-0.01～0.05 mm逐渐增大时，发生接触的钢球数减少，但是相应的接触载荷增大，所以摩擦力矩没有明显变化。

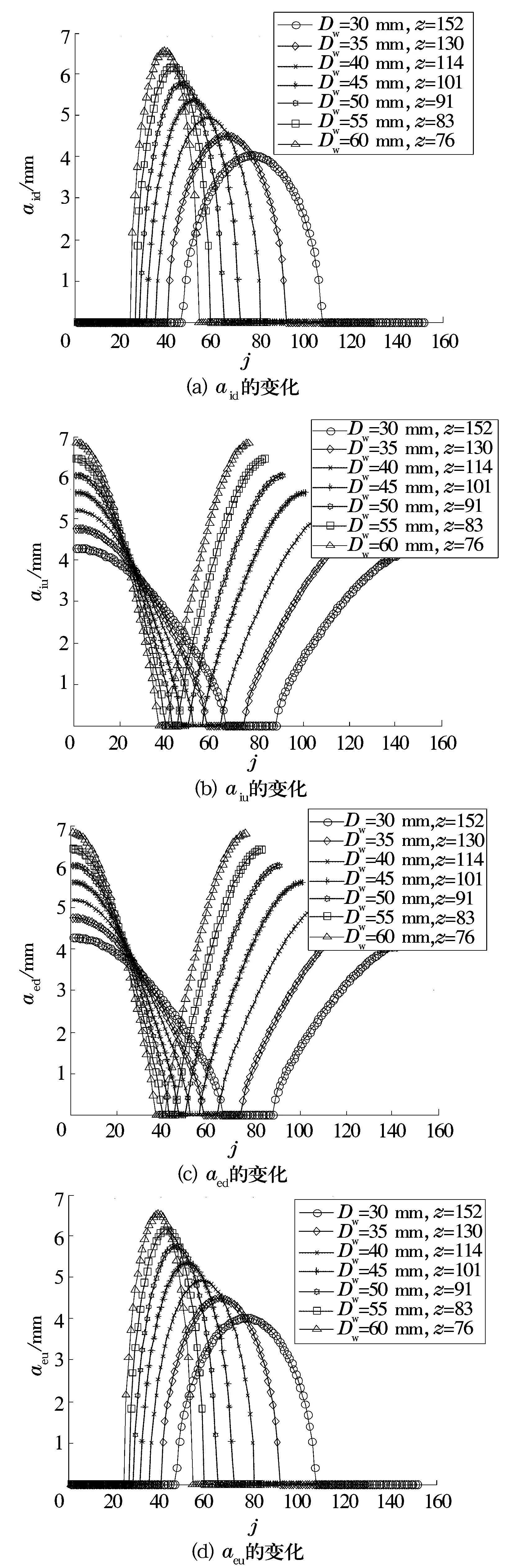
图9 钢球直径Dw对接触椭圆长半轴的影响

综合图2、图4和图7可知，在零游隙的情况下，沟曲率半径系数对球与沟道之间的摩擦力矩影响最大，初始接触角次之，而钢球直径的影响很小。

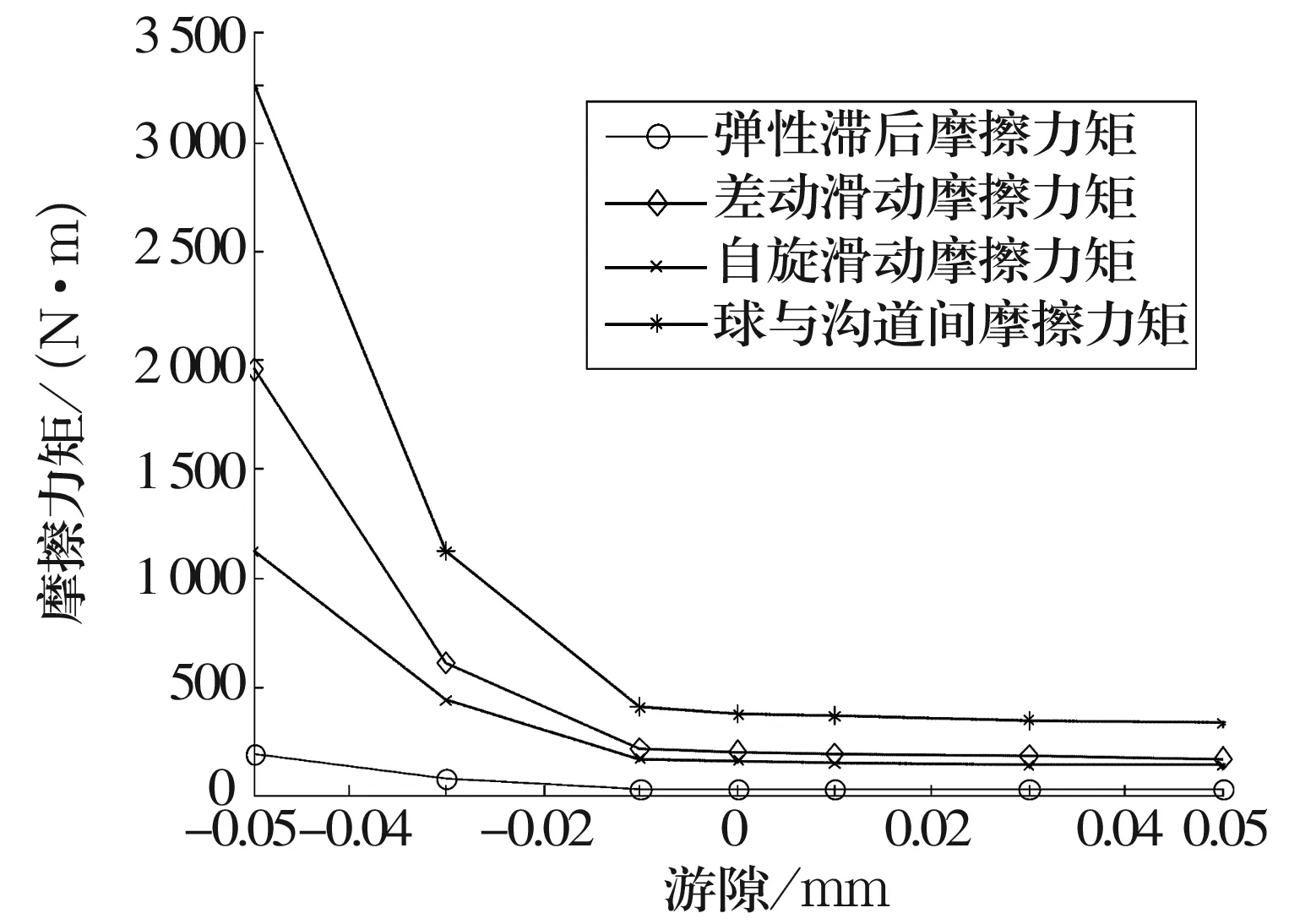
图10 游隙对摩擦力矩的影响

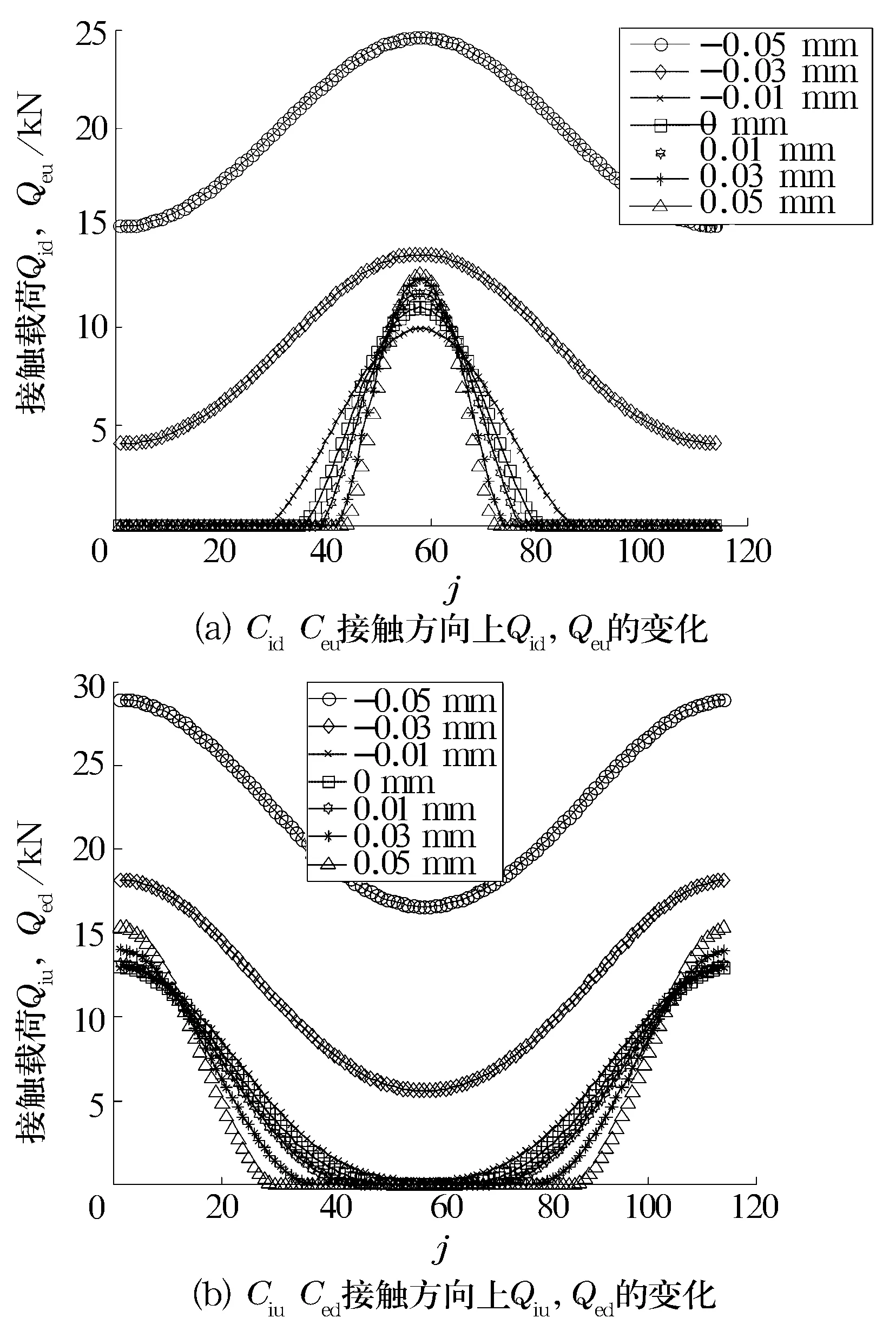
图11 游隙对接触载荷的影响

3 结论

(1)当初始接触角在40°～60°逐渐增大时，四点接触球转盘轴承的球与沟道间的摩擦力矩逐渐减小，而且球与沟道间的接触载荷也减小。通常转盘轴承的接触角为45°，经计算，认为在承载能力允许的情况下，可以考虑将初始接触角取50°～60°，有利于减小轴承的最大接触载荷，提高轴承的承载能力，减小摩擦力矩和轴承生热，从而提高轴承的使用寿命。当然，在实际工程应用中设计初始接触角还应综合考虑转盘轴承的实际受载情况，工程经验表明径向力相对轴向力的比例增大时，应适当减小初始接触角。

(2)当沟曲率半径系数在0.51～0.54逐渐增大时，球与沟道间摩擦力矩逐渐减小，但是球与沟道间的接触载荷增大的幅度不大，因此在轴承设计时可以考虑在0.53～0.54选取沟曲率半径系数。

(3)当钢球直径在30～60 mm逐渐增大时，球与沟道之间的摩擦力矩变化幅度很小，但是随着钢球直径的增大，钢球的数目减少，球与沟道间的接触载荷明显增大，因此在轴承设计时应选用较小的钢球直径。

(4)当游隙在-0.05～-0.01 mm逐渐增大时，球与沟道之间的摩擦力矩急剧减小；当游隙从-0.01～0.05 mm逐渐增大时，摩擦力矩没有明显变化，但是最大接触载荷逐渐增大。因此在轴承设计时建议游隙为-0.01～0.01 mm，有利于提高轴承的承载能力与寿命。

(5)在零游隙的情况下，沟曲率半径系数对球与沟道之间的摩擦力矩影响最大，初始接触角次之，而钢球直径影响很小。