PDE融合方法的两种离散方案的比较研究

刘凯，寇正，罗立民

1.东南大学计算机科学与工程学院，南京 210096

2.解放军理工大学气象海洋学院，南京 211101

PDE融合方法的两种离散方案的比较研究

刘凯1，2，寇正2，罗立民1

1.东南大学计算机科学与工程学院，南京 210096

2.解放军理工大学气象海洋学院，南京 211101

1 引言

近年来，图像融合技术特别是像素级图像融合技术得到了迅速的发展，从经典的基于金字塔变换的方法[1-4]到基于多尺度几何分析的方法[5-8]，可以说图像融合算法层出不穷。Pop.S等[9-11]从2007年开始相继发表论文独创性地提出了基于偏微分方程的图像融合方法，他们认为图像融合过程就是对每一幅源图像应用一个基于偏微分方程的演化过程，在演化过程的每一步，保留当前源图像中的相关信息的同时加入其他源图像中的信息，为此他们提出了描述每一幅源图像演化过程的一般连续方程。在与主成分分析（PCA）方法和多分辨率分析（MRA）方法等经典融合方法进行对比实验的结果显示，基于偏微分方程的融合方法生成的融合图像的质量或比经典方法高或与经典方法接近。他们的工作使得基于偏微分方程的图像融合方法成为一类新兴的融合方法，并开辟了偏微分方程应用的新领域，值得广大科研工作者进行进一步深入的探讨和研究。在连续方程被应用之前必须对其进行离散化，Pop.S等采取的离散化方案是逆扩散项采用先计算梯度再求散度的方案，而本文就在原始连续方程的基础上，通过变换和对方程的正则化项进行相应的调整，推导出另一种形式的方程，将原先的离散化方案变化为计算拉普拉斯的离散化方案，并且将两种方案进行比较。

2 基于偏微分方程的图像融合算法

Pop.S等提出了一个一般连续的源图像的演化方程。

2.1 一维连续方程

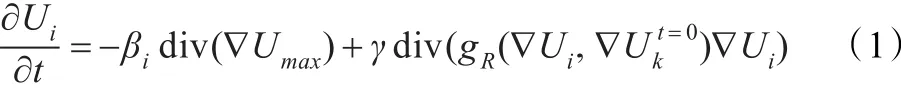
方程（1）右边第一项称为融合项，也被称为逆扩散项，其目的是将其他源图像中的相关信息加入到当前源图像中。式中，div（）是散度算子，i代表当前源图像，max代表具有最大梯度绝对值的源图像，βi为正的权系数。

对当前像素而言，如果最大梯度绝对值出现在当前源图像中，则当前像素不变(βi=0)；否则，如果最大梯度绝对值在其他源图像中被检测到，则梯度以逆扩散过程的方式加入到当前图像中。

方程（1）右边第二项为正则化项，其目的是避免模型产生振荡，因为如果方程中只有逆扩散项可能会导致振荡和不稳定，需要对方程施加约束条件，约束条件就以正则化项表示。式中，γ是正的正则化权系数，其设定正则化项的重要性，gR是一个分段线性函数。正则化项的形式完全取决于融合项，若令gR=1，其形式完全与融合项等同，它的作用相当于一个梯度极值约束（文献[9-11]），使积分过程中方程右端的量值不超过完全由初始梯度极值计算的融合项。

同时方程（1）也表示了一幅图像的演化过程，此方法的机制是每一幅输入的源图像都进行这样的演化过程，在经过一个时间步长后所有图像同步更新数据。区别与传统融合方法的是此算法使得每个源信号都会产生一个输出，当所有输出几乎达到相等时，可以认为融合完成。因此融合的过程实际上也是输出信号之间均方根误差（RMSE）随时间不断减小的收敛过程。

2.2 数值化方案

方程（1）的离散化方案为：

ma代表当前像素的最大前向和最大后向差分绝对值所在的源图像。

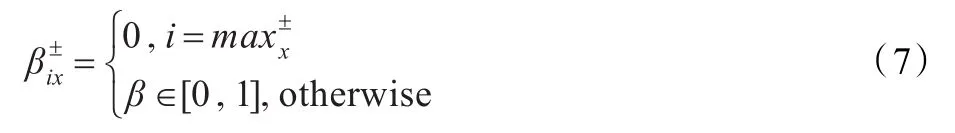
方程（3）显示了div(∇Umax)项的离散化过程，首先，对当前像素检测最大前差绝对值(ma)和最大后差绝对值(ma)，如果ma或ma发生在当前源图像中，则=0或=0；否则，∈[0,1]或∈[0,1]。考虑到在所研究

的邻域内，ma和ma可能出现在不同的源图像中，那么，βi就可能有两个值。然后，前项减后项得到散度。

3 新的融合方法

3.1 连续方程

根据数学定义，方程（1）的右边第一项就是：

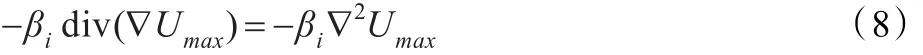
式中，∇2()是拉普拉斯算子，max代表具有最大拉普拉斯绝对值的源图像。

方程的正则化项也根据第一项进行相应调整，这样方程（1）就变换为：

方程（9）的第一项和第二项仍然为融合项和正则化项，但与方程（1）不同的是，方程（9）反映了融合图像中的每一像素的信息是由具有最大拉普拉斯绝对值的源图像提供。参照方程（1）中第二项的形式，也给方程（9）添加一个拉普拉斯极值约束，即方程（9）右端第二项。

3.2 数值化方案

[12-13]中的离散化方案，拉普拉斯算子∇2Umax的离散为：

方程（12）说明了在新方法中对div(∇Umax)的离散化过程，就是对当前像素直接检测拉普拉斯的最大绝对值()，如果出现在当前源图像中，βi=0；否则，βi∈[0,1]。

两种融合方法的区别就在于对逆扩散项的离散化方案，原方法中是通过先计算梯度再求解散度的方案，而在新方法中是直接计算拉普拉斯。

数值积分过程均采用了固定边界条件。

4 两种方案的比较与分析

4.1 一维情形下的比较

为了清楚地反映两种方案的不同作用效果，将两种方案分别应用于两个一维信号的融合，为什么选择在一维情形下进行比较，因为一维信号简单、只涉及一个方向，可以清楚地看到两种方案在运行过程中的差异。这里假定信号A为零，信号B分别为方波、梯形波和三角波，使用两种方案将信号A和信号B进行融合。图1和图2分别是应用原方案和新方案将零与方波融合时信号的演化过程。图3是两种方案在信号融合过程中两信号均方根误差的变化曲线。图4和图5分别是应用原方案和新方案将零与梯形波融合时信号的演化过程。图6是两种方案在信号融合过程中两信号均方根误差的变化曲线。图7和图8分别是应用原方案和新方案将零与三角波融合时信号的演化过程。图9是两种方案在信号融合过程中两信号均方根误差的变化曲线。上述所有一维信号实验的参数设置是相同的，即gF=1,β=1,γ=1,dt=0.1。

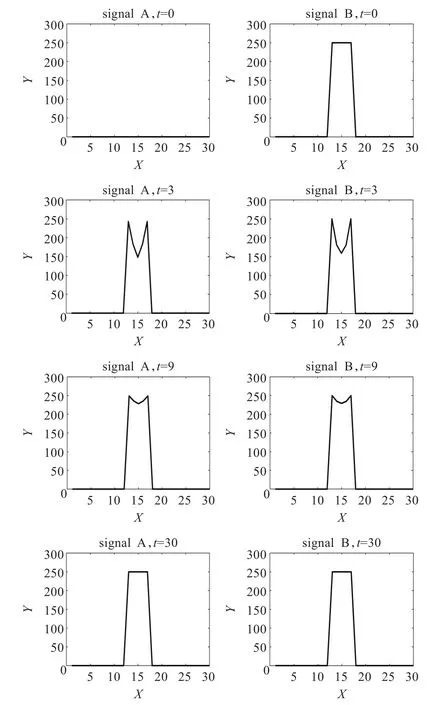
图1 应用原方案将信号A与方波融合的信号演化过程

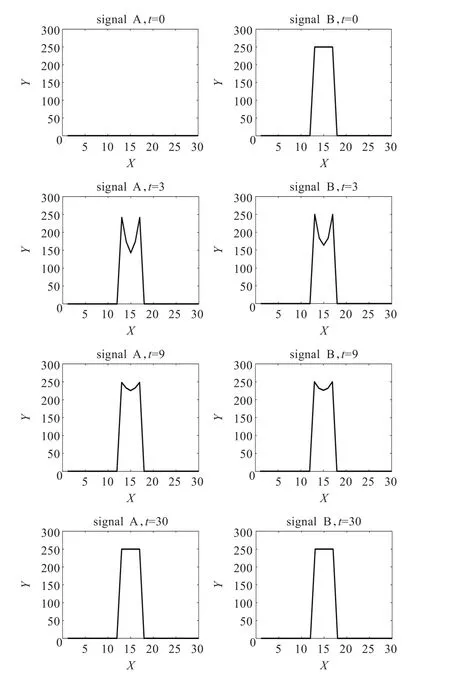
2 应用新方案将信号A与方波融合的信号演化过程

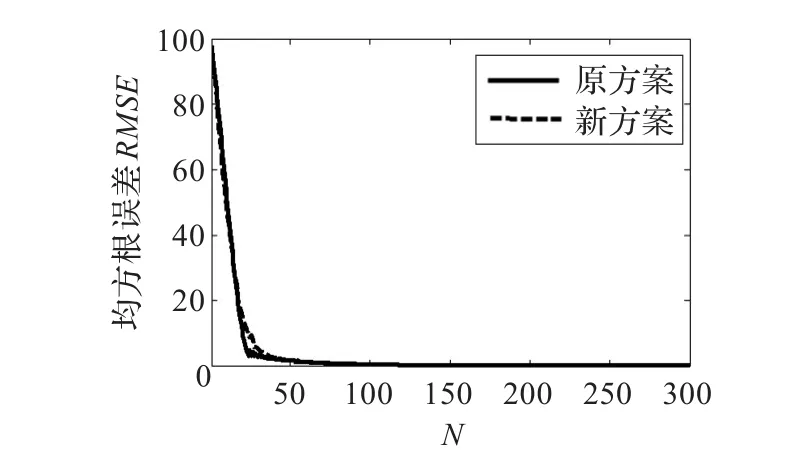
图3 两方案对零和方波信号融合时的均方根误差变化曲线

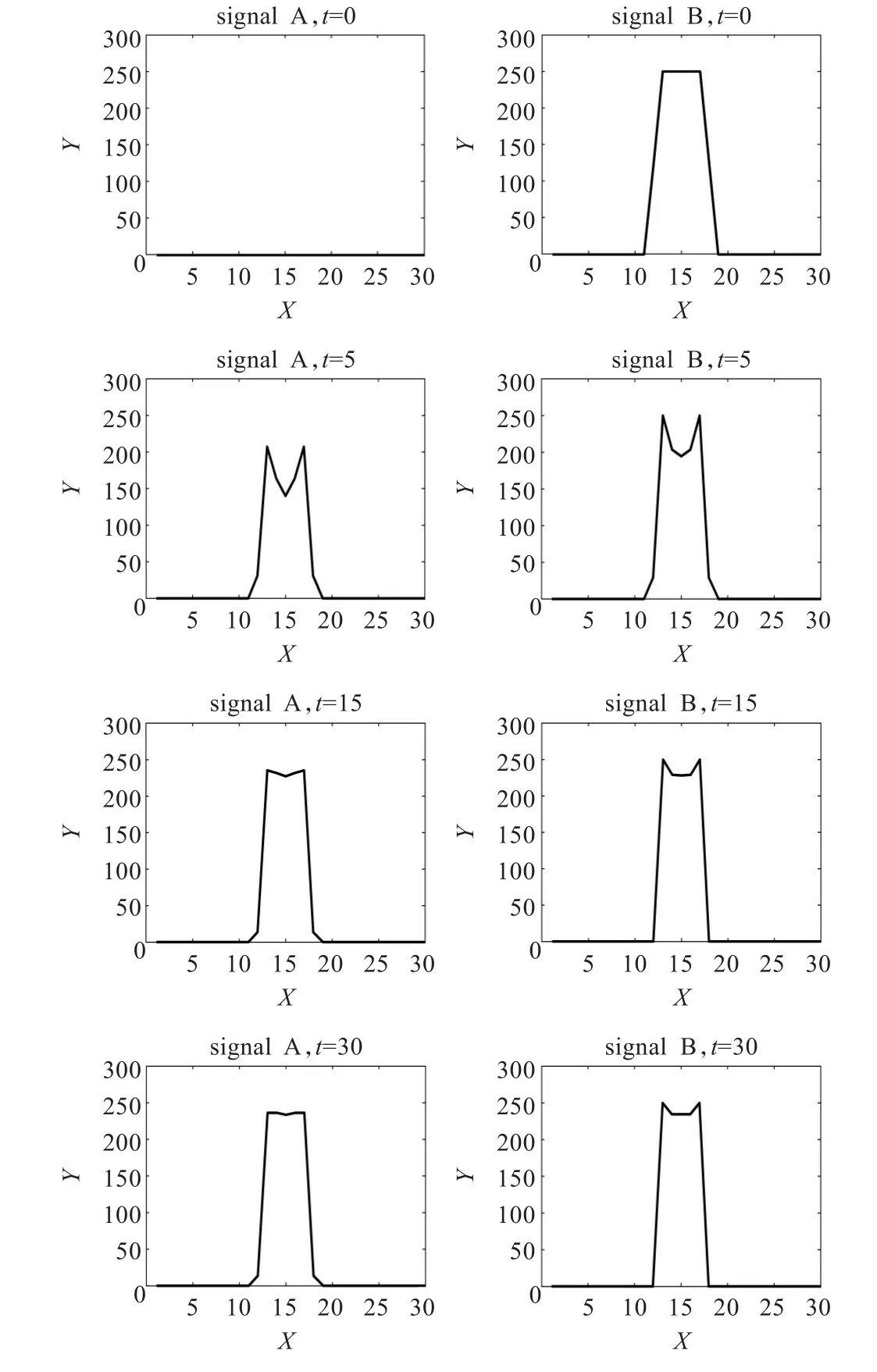
图4 应用原方案将信号A与梯形波融合的信号演化过程

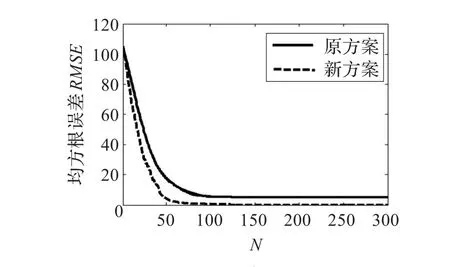
图6 两方案对零和梯形波信号融合时的均方根误差变化曲线

由图1和图2所示，两种方案对零与方波的融合演化过程中在各时刻信号的变化和波形都是十分相似的，当t= 30时，基本都完成了两信号的融合。再由图3所示，两方案的RMSE变化曲线几乎重合，收敛速度几乎相等，可以说两种离散化方案对零与方波的融合几乎没有差别。但当信号B为梯形波时，由图4和图5所示，应用新方案比原方案融合的速度快。对新方案，当t=30时，信号A和信号B都演化成梯形波的波形；而与此同时，对原方案，信号A和信号B都还没有演化到梯形波的波形。这一点也由图6得到证实，如图6所示，新方案的RMSE比原方案下降得快，在t=30时已经下降到0，新方案加速了收敛过程。当信号B为三角波时，情形与梯形波时类似，由图7～图9所示，应用新方案也是比原方案融合的速度快，新方案明显加速了收敛过程。

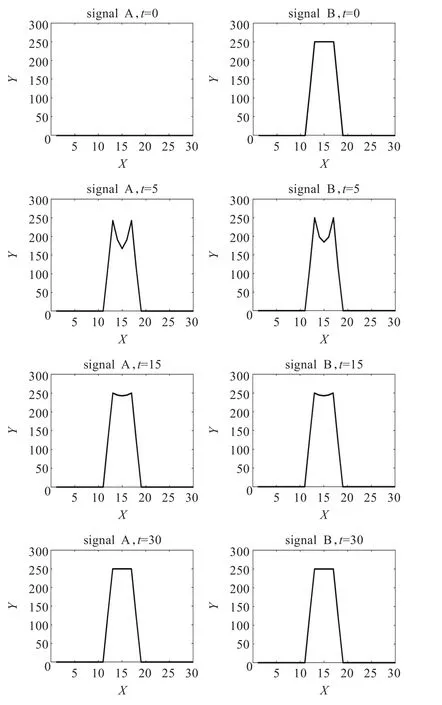
图5 应用新方案将信号A与梯形波融合的信号演化过程

从上面的三组信号的实验结果可以发现，两种离散化方案对突变信号（例如方波）的融合效果基本相同，差别很小。但对缓变信号（例如梯形波、三角波）时，新方案比原方案收敛速度要快。

4.2 二维情形下的比较

将两种方案扩展到二维，分别从x和y两个方向进行计算，比较两种方案对二维图像的融合效果。选择了两组经常用于融合实验的源图像，一组是聚焦不良图像，另一组是医学图像。参考文献[11]将新方案与原方案从融合图像质量指标和算法的收敛性两个方面进行比较，为了定量比较融合图像的质量，选用Piella等[14]提出的加权融合图像质量评价指标Qw，Qw值越大，融合图像的质量越高。算法的收敛性比较上，仍然采用输出图像的均方根误差（RMSE）的演变曲线来分析、比较，RMSE下降越快，说明算法的收敛越快；RMSE值越小，说明输出的图像越相似。

图7 应用原方案将信号A与三角波融合的信号演化过程

图8 应用新方案将信号A与三角波融合的信号演化过程

图9 两方案对零和三角波信号融合时的均方根误差变化曲线

第一组实验的参数设置：β=0.1，γ=2.4,dt=0.1。第二组实验的参数设置：β=0.5，γ=2,dt=0.05。

图10（a）、图10（b）和图11（a）、图11（b）分别为第一组和第二组融合实验源图像。图10（c）、图10（d）和图11（c）、图11（d）分别是采用原方案和新方案经过1 000次迭代后得到的融合图像。图10（e）、图10（f）和图11（e）、图11（f）分别是两组源图像的两种方法的Qw随迭代次数N和RMSE随迭代次数N的变化曲线，其中实线代表原方案，虚线代表新方案。

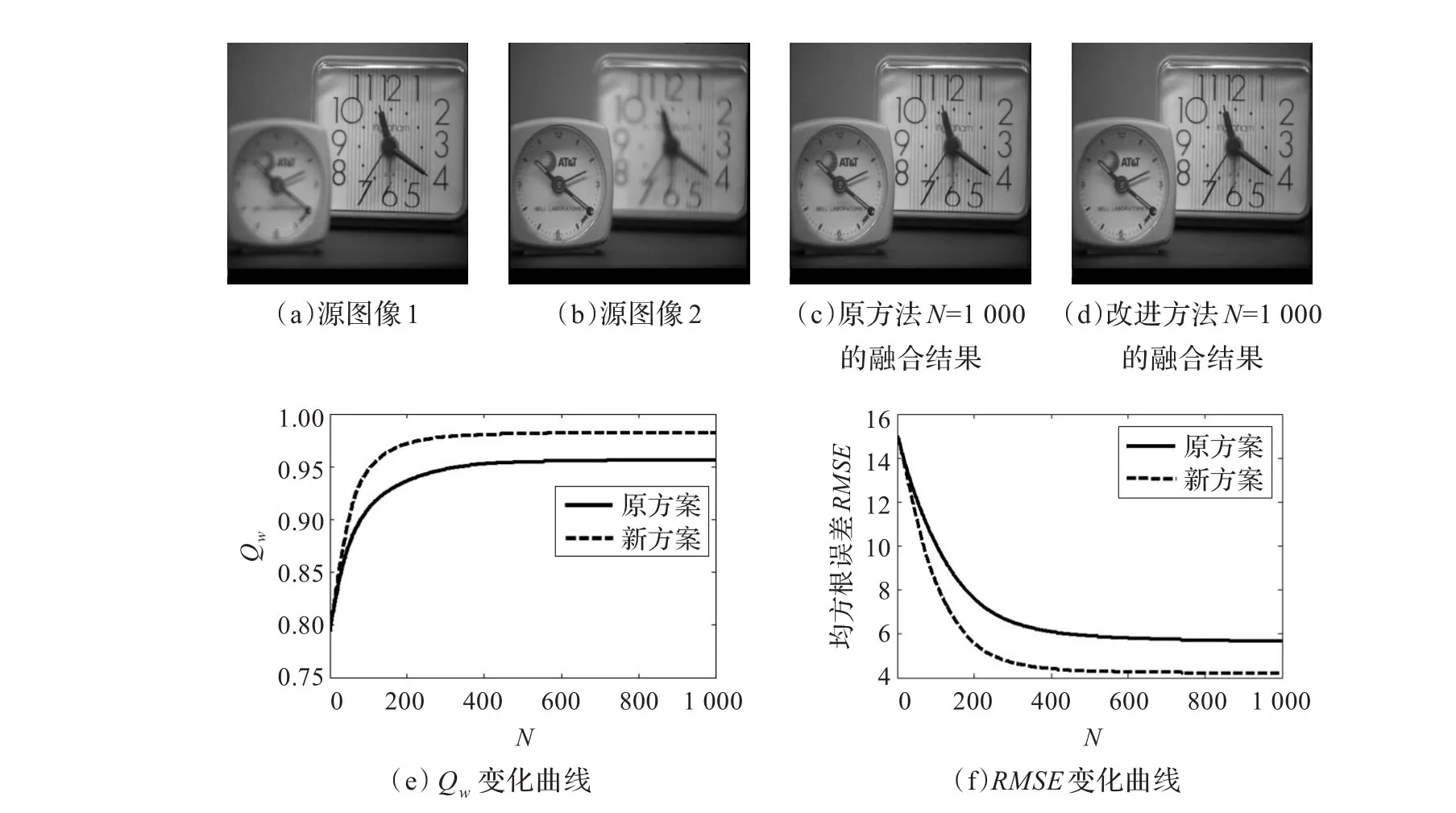
图10 第一例融合实验结果

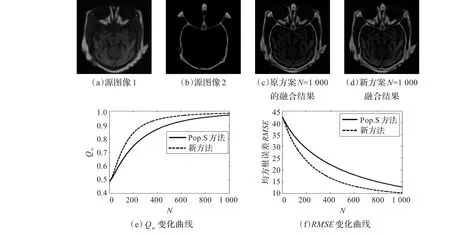
图11 第二例融合实验结果

就第一例实验而言，由图10（c）和图10（d）所示，相对于源图像，无论是原方案还是新方案经过1 000次迭代后输出的融合图像都取得了良好的视觉效果，源图像中模糊的区域经过融合后都消除了模糊，变得清晰了。从质量指标Qw看，由图10（e）中的实线和虚线所示，刚开始随着迭代次数N的增加，两种方案的Qw都迅速上升，提高很快，而新方案的虚线更陡直，即新方案的Qw上升速度更快一些，Qw值也略高，说明采用新方案融合图像的质量比采用原方案的图像质量略好，同时经过较少的迭代次数，就能达到和采用原方案同样的质量指标。当迭代次数N超过300后，随着迭代次数N的增加，Qw都上升缓慢，并且在此之后近似保持不变，但采用新方案的Qw值也总是比采用原方案的略高。而且从两曲线的走势看，随着迭代次数的继续增加超过1 000次后，可以推断采用新方案的融合图像的质量始终比采用原方法的图像质量略好。再从算法的收敛性上看，由图10（f）中的实线和虚线所示，刚开始随着迭代次数N的增加，两种方案的RMSE都迅速下降，但虚线比实线下降得更快，RMSE值更小，说明采用新方案输出图像收敛更快，输出图像更相似；同样当迭代次数N超过300后，两种方案的RMSE都下降非常缓慢，并基本保持不变，但采用新方案的RMSE值总是比采用原方案的RMSE值小，说明如果经过相同次数的迭代，采用新方案的输出图像比采用原方案的输出图像更相似。

对第二例实验而言，由图11（c）和图11（d）所示，同样相对于源图像，两种方案下经过1 000次迭代后输出的融合图像也都取得了良好的视觉效果。由图11（e）中实线和虚线所示，经过1 000次迭代后，采用两种方案的融合图像的Qw都很接近于最大值1。但是在这之前，虚线比实线更陡直一些，采用新方案的Qw上升得略微快一些，说明采用新方案经过较少的迭代次数N，就能达到较高的质量指标。再从算法的收敛性上看，经过1 000次迭代后，采用新方案的RMSE随着迭代次数N的增加，下降得更快一些，输出图像也更相似，说明其收敛性更好。

从两例实验的结果看，总的来说，在相同的参数设置条件下，不论从质量指标还是收敛性上，新方案都比原方案有所提高。

4.3 两种方案得到不同结果的原因分析

为什么对某些信号新方案比原方案结果好?就融合项和正则化项分别进行分析。首先看融合项，在连续情况下，-∇2U=-div(∇U)，而在原方案中相应融合项离散化形式为：，新方案离散化形式为：发生在不同源图像中，原方案前后两项则包含了不同源图像的信息，也就不严格等于拉普拉斯了。然而在新方案中，直接检测当前像素邻域内拉普拉斯的绝对值()，该项必然只包含一个源图像的信息，是严格意义的拉普拉斯项。再看正则化项，正则化项前面已说明，它的作用是梯度（拉普拉斯）极值约束。如果在原方案中保持融合项不变，改变正则化项，采用Laplace正则化，以信号A与梯形波融合为例，如图12所示，两信号也可以很好地融合，但其RMSE变化曲线与原方案非常接近，没有明显改进。而在新方案中融合项采用Laplace，正则化项采用Laplace正则化，如图12所示，新方案的RMSE明显比原方案下降，这说明融合项的新的离散化方案是导致新方案比原方案优越的主要原因，而两方案中的正则化项虽然形式不同，但不是造成两种方案差异的根本原因。

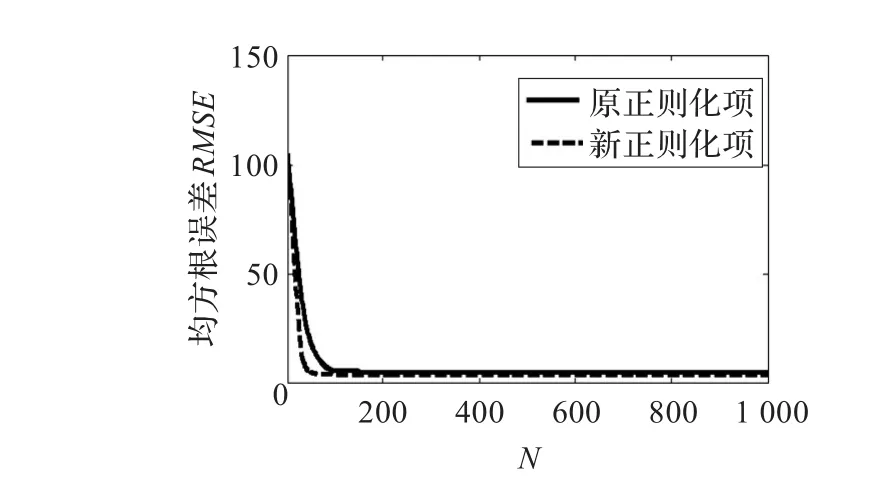
图12 均方根误差变化曲线

5 结束语

在本文中，通过对原始连续方程的变换，提出了基于偏微分方程的图像融合新的离散化方案，新方法的融合策略是融合图像的每一像素的信息，是由处于该位置的具有最大拉普拉斯绝对值的源图像的像素提供的。在一维信号和二维信号融合实验的结果显示，在参数设置相同条件下，新方案一般都比原方案的收敛要快，输出图像的质量指标也略高。

参考文献：

[1]Burt P，Adelson E.Laplacian pyramid as a compact image code[J].IEEE Transactions on Communications，1983，31（4）：532-549.

[2]Burt P.The pyramid as a structure for efficient computation[J]. Multi-resolution Image Processing and Analysis，1984，12.

[3]Toet A，Ruyven L J，Valeton J M.Merging thermal and visual image by a contrast pyramid[J].Optical Engineering，1989，28（7）：789-792.

[4]Toet A.Image fusion by a ratio of low-pass pyramid[J].Pattern Recognition Letters，1989，9（4）：245-253.

[5]Candès E J，Demanet L，Donoho D L，et al.Fast discrete curvelet transforms[J].Multiscale Modeling&Simulation，2005，5（3）：861-899.

[6]Do M N，Vetterli M.The contourlet transform：an efficient directional multi-resolution image representation[J].IEEE Transactions on Image Processing，2005，14（12）：2091-2106.

[7]da Cunha A L，Zhou Jianping，Do M N.The nonsubsampled contourlet transform：theory，design，and applications[J].IEEE Transactions on Image Processing，2006，15（10）：3089-3101.

[8]贾建，焦李成，孙强.基于非下采样Contourlet变换的多传感器图像融合[J].电子学报，2007，35（10）：1934-1938.

[9]Pop S，Terebes R，Borda M，et al.A PDE-based approach for image fusion[C]//Lecture Notes in Computer Science，2007：121-131.

[10]Pop S，Lavialle O，Donias M，et al.A PDE-based approach to 3D seismic data fusion[J].IEEE Transactions on Geoscience and Remote Sensing，2008，46（5）：1385-1393.

[11]Pop S，Terebes R，Borda M，et al.A new discrete PDE-based fusionmodel[C]//EURCON2009，EURCON’09，2009：2075-2082.

[12]陈利霞，宋国乡，丁宣浩，等.改进的总变分去噪算法[J].光子学报，2009，38（4）：1001-1004.

[13]周千，赵芳玲，赵凤群，等.You-Kaveh图像去噪模型扩散系数的改进[J].计算机工程与科学，2010，32（2）：85-87.

[14]Piella G.New quality metric for image fusion[C]//The 7th International Conference on Information Fusion，Stockholm，Sweden，2004：542-546.

LIU Kai1，2,KOU Zheng2,LUO Limin1

1.School of Computer Science&Engineering,Southeast University,Nanjing 210096,China
2.Institute of Meteorology,PLA University of Science and Technology,Nanjing 211101,China

On the basis of the continuous equation of image fusion based on Partial Differentiation Equations（PDE）proposed by Pop.S et al,a new numerical scheme of the equation is presented.The former discrete scheme of divergence by the calculation of gradient is changed to the scheme of the calculation of Laplace,and the regularization term of equation is also adjusted accordingly.The comparison experiments are designed for two schemes on some 1D and 2D signals.The results show that the new scheme can perform the fusion effectively for all the tested signals;and the new scheme can accelerate the convergence process and make the quality of fused image improved by means of a quality factor for some of the tested 1D and 2D signals.However for the other tested signals,the convergence and the quality of output signals obtained by both the new scheme and the former scheme are also very much closed.

image fusion;partial differential equation;discrete scheme;Laplace;gradient

基于Pop.S等提出的基于偏微分方程（PDE）的连续图像融合方程，提出了一种新的离散化方案，将原来的先计算梯度再求散度的离散化方案变化为直接计算拉普拉斯的离散化方案，对方程的正则化项进行相应的调整。将这两种离散化方案分别对一些一维信号和二维信号进行融合对比实验，实验结果显示：对所有的测试信号，新方案都能进行有效的融合；对某些测试的一维和二维信号，新方案能够加速信号的收敛过程并且使得到的融合图像在质量指标上比原方案有提高；而对某些测试信号，新方案与原方案在输出信号的收敛速度上和输出图像的质量指标上也是十分接近的。

图像融合；偏微分方程；离散化方案；拉普拉斯；梯度

A

TP391.41

10.3778/j.issn.1002-8331.1202-0588

LIU Kai,KOU Zheng,LUO Limin.Comparison study of two numerical schemes for PDE-based fusion method.Computer Engineering and Applications,2013,49（24）：165-171.

刘凯（1970—），女，讲师，主要研究方向为气象遥感卫星信息处理、模式识别；寇正（1971—），男，博士，副教授，主要研究方向为大气动力学数值模拟；罗立民，男，教授，博士生导师，主要研究方向为图像图形信息处理。E-mail：liukaiqy@163.com

2012-02-29

2012-07-13

1002-8331（2013）24-0165-07