有源带阻滤波器的综合
孟文晴,李琨,谭玲玲,滕建辅,
1.天津大学电子信息工程学院,天津 300072
2.天津理工大学电子信息工程学院,天津 300384
有源带阻滤波器的综合
孟文晴1,李琨2,谭玲玲1,滕建辅1,2
1.天津大学电子信息工程学院,天津 300072
2.天津理工大学电子信息工程学院,天津 300384
1 引言
级联型有源滤波器设计技术已经很成熟,而且可用的二阶节电路也很多,但这些电路是怎么来的?却没有答案。对于无源LC网络,可以根据网络综合理论,由传递函数导出设计导抗,然后由设计导抗综合出电路的拓扑结构和元件值。根据极点移出顺序的不同,一个设计导抗可以对应多个电路拓扑结构。对于有源网络,能否像无源网络那样通过网络综合得到电路的拓扑结构,以及能否通过有源网络综合发现新的有源RC电路,是一个需要解决的理论问题。Haigh经过多年的潜心研究,提出了有源网络综合的基本思路和基本理论[1-4]。但如何根据这些基本理论,由传递函数导出电路的拓扑结构,仍需要进一步研究。本文应用有源网络综合的基本理论,研究如何由符号传递函数导出RC有源电路,并给出了无限增益多路负反馈型有源带阻滤波器的综合实例。
2 有源网络综合的基本理论
综合法是以网络综合理论为基础的方法,它找出与理想滤波特性相近似的网络函数,然后根据综合方法实现该网络函数,由这种方法设计出来的滤波器,实测的滤波特性与理论计算特性十分接近,所以适合于高精度的滤波器设计要求[1]。该方法将描述特定传输函数的p×p端口导纳矩阵扩展到与其等效的n×n节点导纳矩阵,其中n>p。通过在导纳矩阵中引入代表内部节点的全零行和全零列开始矩阵的扩展,并加入构成有源元件的零器(Nullor),然后应用主元扩展的理论[2],直到导纳矩阵中的每一个元素成为一个单独的导纳元素,Nullor将产生的矩阵元素移动到合适的位置,使其能描述浮动或接地的无源元件[3],最后获得的节点导纳矩阵包含代表无源元件的元素和代表有源元件的元素[4],由此得出满足给定传输函数的电路结构。
2.1 Nullor模型
Nullor是由零子和任意子组成的。零子(nullator)和任意子(norator)的VCR是通过对其端口电压和电流的限定来描述的,零子是约束条件为V1(S)=I1(S)=0的单端口网络,任意子的约束条件是V2(S)=任意值,I2(S)=任意值的单端口网络。Nullor是具有零传输矩阵的两端口网络,即:
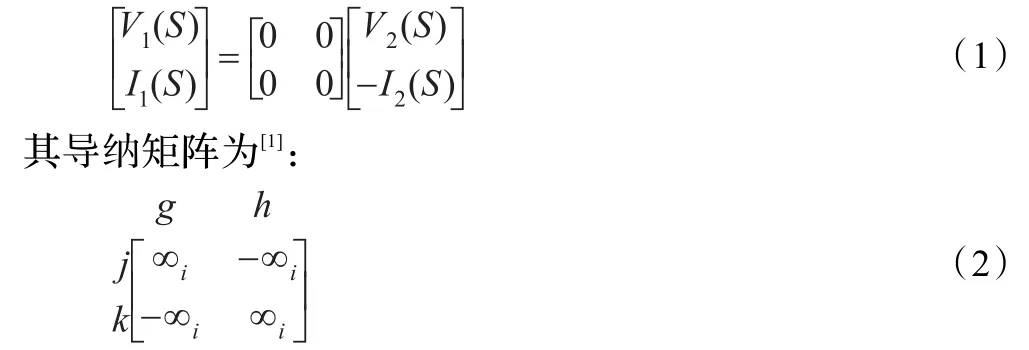
该矩阵表示零子连接在节点g和h之间,任意子连接在节点j和k之间。其中∞i是关联无穷参数,i代表的是第i个Nullor。对于VCVS和CCCS的传递函数,其端口导纳矩阵也包含∞i变量,这样∞i就可以作为端口导纳矩阵到节点导纳矩阵转换的桥梁。
用Nullor构建有源器件的模型,已经有很多的研究[5-7],图1所示的Nullor可以代表理想的运算放大器。
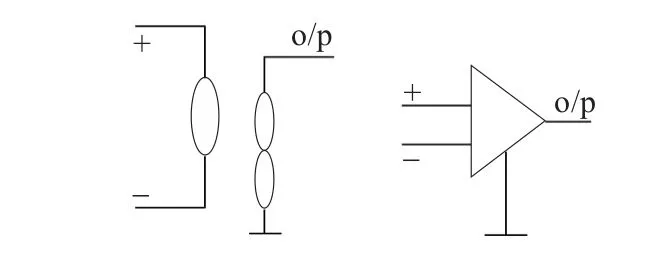
图1 Nullor及与其等效的理想运算放大器
2.2 给定电压或电流传输函数的导纳矩阵表达式
对于VCVS的2×2端口导纳矩阵,可以通过主元扩展到如表1所示的3×3或4×4矩阵。矩阵的行和列依次从1开始标号,节点1和节点2分别为输入和输出节点,并与其他的节点通过交叉直线区分。表1[1]的第一种类型适用于正的传输函数,并且传输函数中分子N包含在分母D中;第二种类型也适用于正的传输函数,但是传输函数中分母D包含在分子N中;第三种类型适用于负的传输函数,并且分子和分母是相互独立的;第四种类型适用于分子或是分母中有正负组合的项。为了得到更高阶的传递函数,表中的矩阵元素可以依据主元扩展理论进行扩展。

表1 实现给定电压传输函数的电路的导纳矩阵
2.3 等效矩阵变换
任意元素定理对于单独的变量∞i,矩阵中的任意有限元素可以加到它所在的行和列的任意位置;对于导纳矩阵中位于同一行或同一列的±∞i,矩阵中的任意有限元素可以加到该行或该列的任意位置[8]。
元素移动定理当±∞i位于矩阵的同一行时,±∞i所在列的其他元素可以在对应列自由移动;当±∞i位于矩阵的同一列时,±∞i所在行的其他元素可以在对应行自由移动。另外,对应非端口节点的元素可以进行尺度变换,并且可以加到任意行或列[8]。
3 有源网络综合的方法
无源RC电路的综合过程[]可以扩展到有源RC电路的综合[]中,综合过程主要分为以下六步:
(1)从表1中选择合适的扩展矩阵。
(2)对照传输函数确定扩展矩阵中的各个元素。
(3)对N、D、P、Q进行扩展,直到所有的函数均为一阶导纳函数。
(4)利用任意元素定理、元素移动定理,引入相应的矩阵元素或移动原有的矩阵元素。
(5)VCVS类型的传输函数通常用于级联的形式。表1是VCVS传输函数的导纳矩阵,第1行为全零行,就意味着它的输入导纳为零,然而VCVS类型的电路的输出导纳趋于无穷,所以当用于级联形式时,可以放松输入导纳为零的限制。

(6)对于矩阵中的±y元素,+y处于对角线位置,-y与+y位于同一行并且在第1列时,可以进行式(3)的矩阵变换,以去除输入导纳为零的限制。
如果所有的矩阵元素现在都能正确地描述无源元件,那么这个电路就是单Nullor电路,否则添加额外的Nullor来引入缺失的矩阵元素[1]:
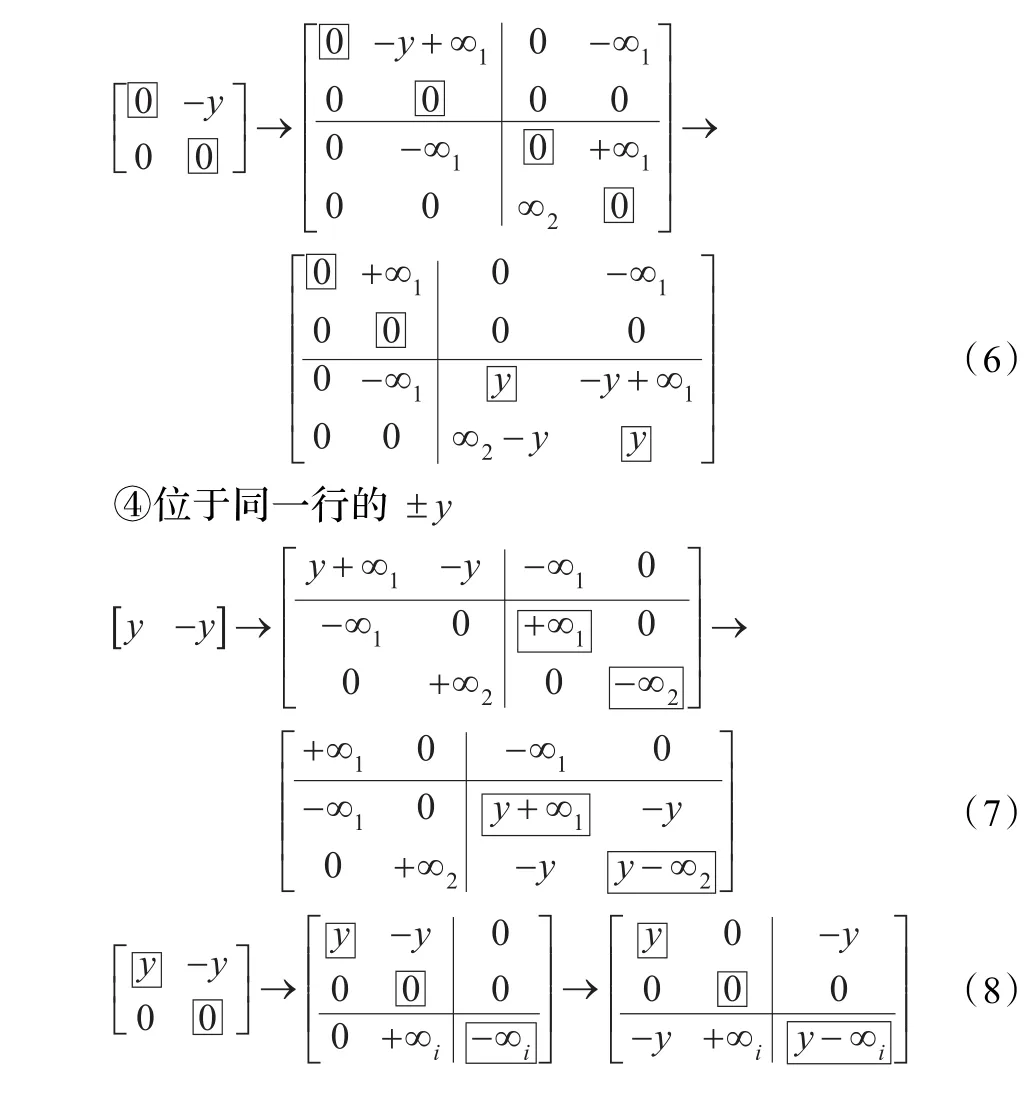
①单个正的非对角线元素y

添加全零行和全零列,并在节点2和3之间引入零子,节点1和3之间引入任意子,利用元素移动定理将y移至主对角线位置。同样的方法适用于②、③、④情况(方括号表示该元素处于对角线位置)。
②单个负的对角线元素-y

4 有源带阻滤波器综合实例
为了得到带阻滤波器,选择的电路的传递函数为式(9):

其中,a、b、d、e、g、h、i、j为电阻,c、f为电容,由于传输函数的分子和分母中有正负组合的元素,所以选定的待扩展矩阵为表1的第四种类型,将式(9)写成:

在选定了传递函数后,确定矩阵中的各个元素:
阵中y51和y55元素进行主元扩展,得到矩阵(13):

式(13)中,∞1和-∞1所在的行可以加上任意的元素,由此引入±j和±e。对于元素±a和±b,由第3章的第(5)步消除输入导纳为零的限制,可以将第零行的±a和±b移至第1行,所以矩阵(13)等价为矩阵(14):
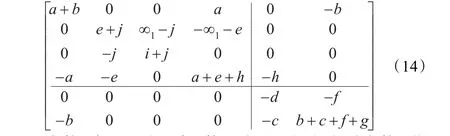
在第5行引入全零行,第6列引入全零列,并在第5节点和参考点间引入任意子,在第6节点和参考点之间引入零子,得到矩阵(15):

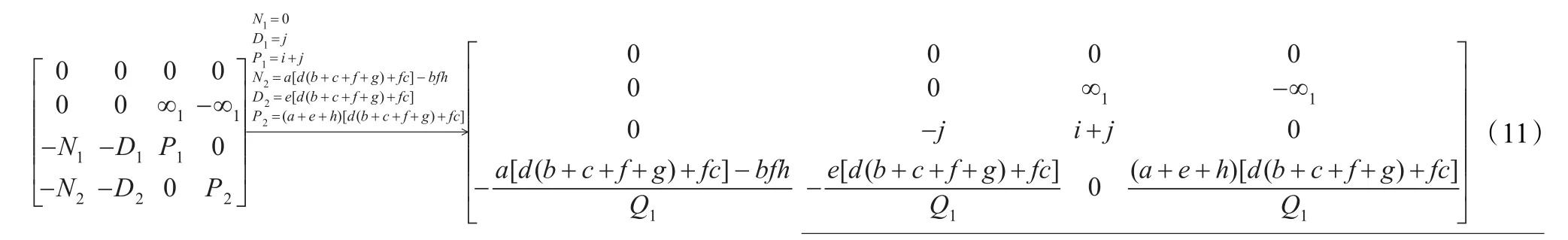
式(11)中引入了任意一阶导纳函数Q1,适当地选取Q1进行主元扩展。选取Q1=d(b+c+f+g)+fc,并对矩阵中元素进行主元扩展,得到矩阵(12):

再次引入一阶导纳函数Q2,令Q2=b+c+f+g,对矩
根据任意元素定理,可以在第5行相应位置引入±c,第5行和第6列的相应位置上引入±d、±h和±f。

从式(16)可以看出,此电路包含两对Nullor,其中一对的零子接在节点3和节点4之间,任意子接在节点2和参考节点之间,另一对的零子接在节点5和参考点之间,任意子接在节点6和参考点之间。因此,综合后的电路结构如图2所示。
在式(1)中,如果选取a、b、d、e、g、h、i、j是电阻,c、f是电容,可以实现二阶带阻滤波器,如图3所示。
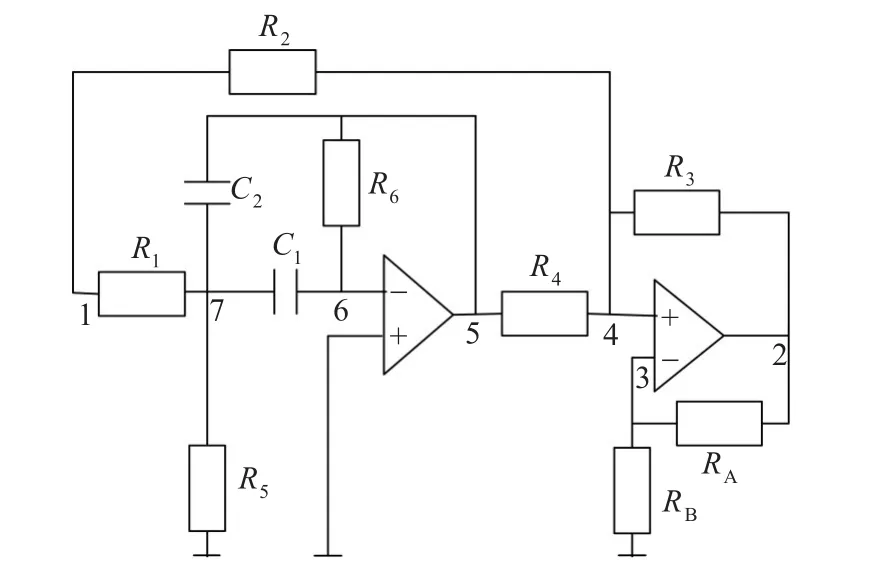
图3 二阶带阻滤波器电路
图3所示电路的传递函数[11]为式(17):

设带阻滤波器的fo=1 kHz,Qp=2,K=2,取C1=C2= 10 nF,R2=R3=R4=15 kΩ,2R1=R6,由式(18)和式(19)可得R1=31.85 kΩ,R6=63.69 kΩ,R5=4.55 kΩ。取RA=RB=10 kΩ,所实现的电路如图4所示。
通过SPICE仿真,得到最终仿真结果如图5所示;实测结果如图6所示。实测过程中通过改变R5、R6、C1和C2的值,发现元件误差会导致滤波器中心频率及衰减特性发生偏差,因此经过精细调节可以实现。
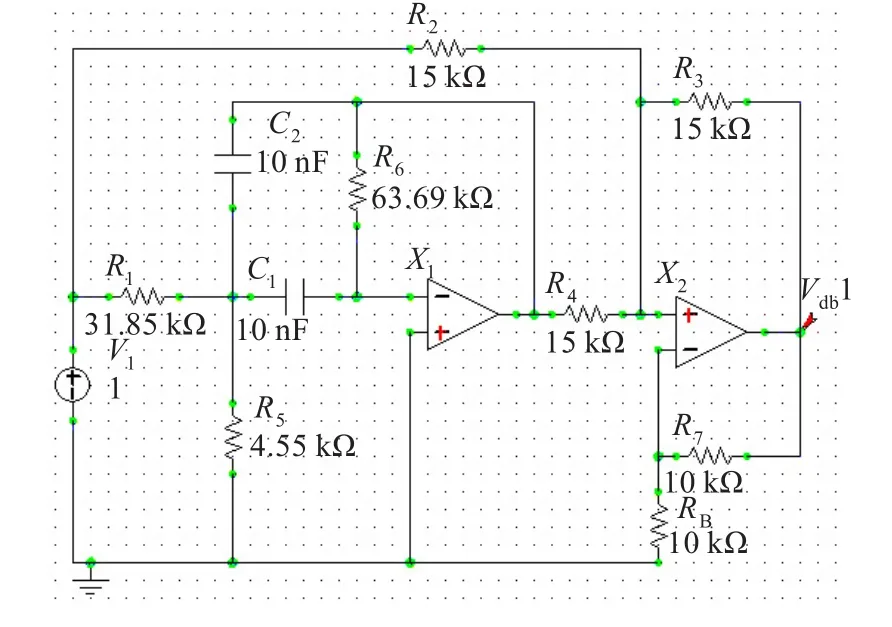
图4 二阶带阻滤波器电路图
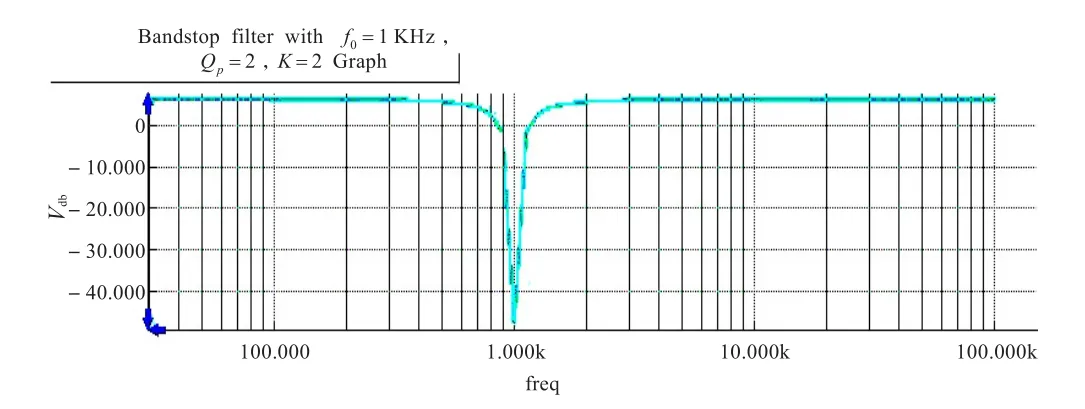
图5 二阶带阻滤波器仿真
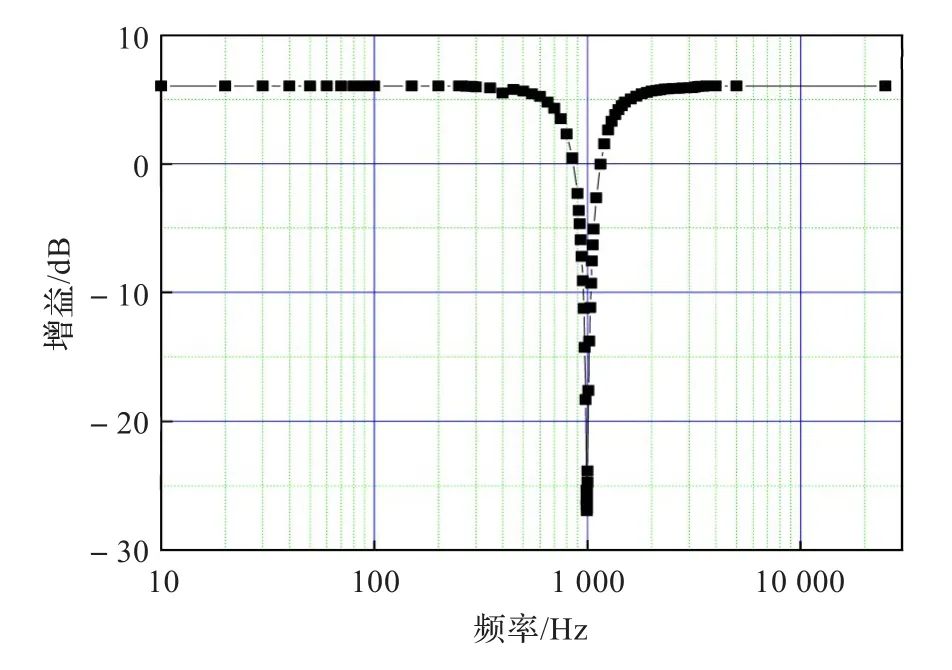
图6 二阶带阻滤波器实测曲线
5 结论
对于一个较为复杂的传递函数,灵活运用有源RC网络综合的方法,对矩阵进行了主元扩展,导出了新的二阶RC带阻滤波器电路。不同于其他的电路综合方法,本文方法从数学的角度出发,不对电路结构做任何推测,从传输函数的端口矩阵,通过主元扩展到节点导纳矩阵,最后得出电路结构。
[1]Haigh D G.A method of transformation from symbolic transfer function to active-RC circuit by admittance matrix expansion[J].IEEE Trans on Circuits Syst I,Reg Papers,2006,53(12):2715-2728.
[2]Haigh DG,Radmore P.Systematic synthesis method for analogue circuits-Part I notation and synthesis toolbox[C]// Proceedings of the International Symposium of Circuit and System(ISCAS),May 23-26,2004:701-704.
[3]Haigh D G,Clarke T J W,Radmore P M.Symbolic framework for linear active circuits based on port equivalence using limit variables[C]//Proceedings of the International Symposium of Circuit and System,Sept 2006,53:2011-2024.
[4]Haigh D G,Tan Fangqun,Papavassiliou C.Systematic synthesis method for analogue circuits-Part III all-transistor synthesis[C]// Proceedings of the International Symposium of Circuit and System(ISCAS),May 23-26,2004:701-712.
[5]Wang Hungyu,Huang Wenchung,Chiang Nanhui.Symbolic nodal analysis of circuits using pathological elements[J].IEEE Transaction on Circuits and Systems,Nov 2010,57:874-877.
[6]Fernandez S L,Tan T C.Pathological element-based active device models and their application to symbolic analysis[J]. IEEE Transaction on Circuits and Systems,Jun 2011,58: 1382-1395.
[7]Soliman A M.Two integrator loop filters:genertation using NAM expansiom and review[J].Journal of Electrical and Computer Engineering,2010(1).
[8]Haigh D G.Symbolic active-RC circuit synthesis by admittance matrix expansion[J].IEEE Trans on Circuits Syst I,Reg Papers,2005(1):248-251.
[9]Haigh D G,Radmore P M.Symbolic rassive-RC circuit synthesis by admittance matrix expansion[J].IEEE Trans on Circuits Syst I,Reg Papers,2005(1):244-247.
[10]Soliman A M.Applications of voltage and current unity gain cells in nodal admittance matrix expansion[J].Circuit and System Magazine,2009,9(4).
[11]谭玲玲,滕建辅,刘开华,等.有源RC滤波器网络的综合[J].电路与系统学报,2011,16(5):30-35.
MENG Wenqing1,LI Kun2,TAN Lingling1,TENG Jianfu1,2
1.School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China
2.School of Electronic Information Engineering,Tianjin University of Technology,Tianjin 300384,China
The design technique for cascaded active filter is mature,but the synthesis of biquadratic circuit is still need to be further studied.Based on the theory of active network synthesis,a method of new active circuit synthesis is given which uses symbolic voltage transfer function and linked infinity variables to describe both Nullors in the nodal admittance matrix and port admittance matrix of a synthesized circuit.The circuit topology is derived by admittance matrix expansion.A new 2nd-order active-RC bandstop filter synthesis example is presented by using privotal expansion on the port matrix.The simulation and the measured results verify the correctness of the given method.
active network synthesis;Nullor;admittance matrix;bandstop filter
级联型有源滤波器的设计技术已经非常成熟,但二阶节电路的综合是尚未解决的难题。根据有源网络综合理论,给出了有源电路新拓扑结构的综合方法。该方法通过给定的电压符号传输函数,使用关联无穷变量来描述被综合电路中节点导纳矩阵和端口导纳矩阵中的零子和任意子,通过导纳矩阵的扩展导出电路的拓扑结构。这种方法可以综合出新的电路结构;给出了二阶有源带阻滤波器新电路的综合实例。仿真和实测结果验证了该方法的正确性。
有源网络综合;Nullor模型;导纳矩阵;带阻滤波器
A
TN911.7
10.3778/j.issn.1002-8331.1112-0623
MENG Wenqing,LI Kun,TAN Lingling,et al.Synthesis of active bandstop filter.Computer Engineering and Applications, 2013,49(19):213-216.
孟文晴(1986—),女,硕士研究生,研究方向为滤波器电路综合,射频电路设计,数字信号处理;李琨(1981—),男,博士,讲师,研究方向为滤波器电路综合,射频电路设计,数字信号处理;谭玲玲(1986—),女,硕博连读研究生,研究方向为有源网络综合;滕建辅(1954—),男,教授,博士生导师,研究方向为滤波器的理论与设计,电路设计,信号处理技术。E-mail:mengwenqing@126.com
2012-01-02
2012-03-01
1002-8331(2013)19-0213-04
CNKI出版日期:2012-05-21http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1137.006.html

