基于量子免疫进化的空时多维参数估计

邱新建，李庆华，薛凤凤，彭安洪

1.新疆大学信息科学与工程学院智能信号处理实验室，乌鲁木齐 830046

2.中国人民解放军68203部队

3.空军工程大学电讯工程学院，西安 710077

基于量子免疫进化的空时多维参数估计

邱新建1，2，李庆华1，薛凤凤3，彭安洪1

1.新疆大学信息科学与工程学院智能信号处理实验室，乌鲁木齐 830046

2.中国人民解放军68203部队

3.空军工程大学电讯工程学院，西安 710077

1 引言

人工免疫算法的概念是1996年在日本举行的免疫系统国际会议上首次提出的，国内，西安电子科技大学的焦李成教授已经将其发展成为了一个完备的理论体系，并且不断提出新的免疫算法。人工免疫进化算法的应用研究是其中一个重要的研究方向，目前它在目标优化、机器人控制、神经网络设计等领域已有着广泛的应用，而在多维参数估计领域研究还较少。文献[1]将免疫算法用于解决频率估计和方位角的估计的问题，文献[2]用免疫进化算法解决高斯—牛顿算法的二维搜索问题。多维参数估计是空间谱估计理论应用中的一个重要课题，精典的参数估计大多是针对方位的一维信号参数（方位角）的估计，当然也很容易推广到二维（方位角和俯仰角）甚至多维（频率、方向角及俯仰角），但此时计算量、数值稳定性等问题就显现了出来，如多维MUSIC算法，以及基于高阶累积量的MUSIC算法都存在这一问题。ESPRIT算法虽然使DOA估计算法的计算量降了下来，但是它在低信噪比的情况下性能欠佳，往往达不到实际应用的要求。本文通过理论分析将高效的量子免疫进化算法与多维参数估计问题结合起来，使得算法的性能得到了很大的提高。

2 量子免疫进化算法

量子免疫进化算法[3-6]主要是一种借鉴自然界生物免疫系统的克隆选择和亲和力成熟原理的人工算法，克隆选择对应着一个亲和力成熟的过程，即对抗原亲和力较低的个体在克隆选择机制作用下，经历增殖复制和变异操作，使其亲和力逐步提高而“成熟”。新个体的产生主要由克隆选择、增殖和高频变异来完成。

2.1 个体的编码

本文采用量子染色体编码，假如共用了n个量子染色体，每个染色体采用m位量子编码，则用前m/2位表示方位角而后m/2位表示俯仰角，每一位量子编码包含一对量子比特幅度，表示为量子染色体可以转化成二进制染色体，产生一个在0和1之间的均匀分布的随机数λ，若λ＜|2，则二进制染色体取0，否则取1。

2.2 克隆选择、增殖、高频变异

克隆选择就是对各个染色体进行克隆增殖，增殖的数量与该染色体与抗原的亲和力值有关，亲和力值越高的染色体拥有越多的增殖副本，并根据它们的亲和力值进行变异，为了保存亲和力值较高的副本，亲和力值越高，变异概率越小。

2.3 算法终止条件

算法终止一般分为达到设定最大进化次数时停止和改进量小于阈值时停止两种。达到最大进化次数停止就是当算法达到了提前设定的进化次数时就停止，改进量小于阈值时停止就是当前一代染色体与下一代染色体与亲和力值的差值小于一个设定的ε时，算法停止。

3 阵列信号分析

设信号接收阵列为平面阵，阵列模型如图1所示。

图1 阵列模型图

图1中子阵X位于x轴上，子阵Y位于y轴上，两个子阵的结构是完全相同的，均为等距离均匀线阵，且阵元数均为M。以原点处的阵元为参考点，空间信号照射到平面阵上的俯仰角用φ表示，方位角用θ表示。根据时域延迟与空域延迟的相通性与特殊性，两者在一定的条件下可以相互的转换，则第i个信号到第m个阵元与第i个信号到参考阵元相比，时延为：

现设线阵为X，阵源数为M，沿x轴以间距d从原点依次排开，将X阵输出的数据记为X1(t)。现将X1(t)再进行τ个单位的延迟，延迟后的数据记为Z1(t)，则有：

由(Cx11，Cz1x1)组成一个矩阵束，根据矩阵束的秩与广义特征值分解的关系可得e-j2πfiτ(i=1，2，…，N)是此矩阵束的广义特征值[7]，设其值为tfi，则有：

根据信号子空间拟合理论，可得空时二维谱估计的谱可由下式求得：

4 算法基本步骤

步骤1初始化种群，设置染色体的个数、维数、克隆数目、变异幅度、进化代数等参数，按量子染色体编码规则编码，并将量子染色体转化为二进制染色体。

步骤2亲和力值的计算，将阵列接收的信号组成流型矩阵A1，将步骤1得到的二进制染色体转化成十进制，估计协方差矩阵ˆ，然后按式（10）计算所有抗体对抗原的亲和力函数值P。

步骤3克隆繁殖，对初始抗体种群中的每一个抗体都复制个，K为设定的克隆数目，并排列成一个抗体集合。

步骤4高频变异，对克隆产生的子抗体按照式（11）进行变异，同时父抗体也参与变异操作，并且对变异结果进行挑选，对不在原定义域内的新抗体进行排除。

其中，p=(1/β)e-F，r为上一代抗体，p反比于亲和力值，β用来控制变异幅度。

步骤5抗体选择，对所有符合条件的新抗体计算其亲和力函数值，比较父抗体和各个变异子抗体的亲和力值，并用最大值代替父抗体，形成新的父抗体。

步骤6抑制操作，分别计算每一个抗体种群中抗体之间的相似度，删除相似度小于阈值的一个，保留另外一个。

步骤7如果满足终止条件，则输出所有抗体和其亲和力值，输出抗体所在位置即为三个待估计信号的位置；否则转入步骤8。

步骤8随机生成新抗体，转入步骤2继续迭代。

5 仿真实验

实验以MATLAB 2010b为平台，在CPU Penium-4 2.93 GHz，RAM 512 MB配置的PC机上进行。实验采用16元均匀面阵，阵元间距为半个波长，有3个独立的信号源，平均信噪比设置为-15 dB，快拍数为100，实验次数为10次，方位角、俯仰角、和信号频率分别为（30°，35°，2 GHz），（50°，45°，6 GHz），（60°，55°，10 GHz）。染色体数目设置为65，维数为22，克隆数目K=65，初始变异幅度将步骤7中的终止条件设置为前后两次亲和度函数值的变化量小于某个给定的数，即|F1-F2|＜ε（本文ε取为0.01），同时将进化次数设置为30代，算法达到最大进化次数或者满足终止条件都将停止运行。为了说明本文算法的有效性，将本文算法与二维MUSIC算法[8]进行全面的比较。

图2为本文算法与二维MUSIC算法的均方根误差（RMSE）随信噪比的变化曲线，图3为估计方差随信噪比的变化曲线。

图2 参数估计的RMSE随信噪比的变化曲线图

从图2可以看出，本文算法对方位角和俯仰角估计的均方根误差在大于5 dB后都比二维MUSIC算法小，并且本文算法随着信号比的升高性能迅速的改善，而二维MUSIC改变不大，高信噪比时均方根误差是本文算法的2～3倍，同时频率估计的误差比大部分角度估计都小。从图3可以得到本文算法估计值的方差都较小，说明本文算法估计值的散布范围小，这正是由于二维MUSIC算法对快拍数、信噪比敏感造成的，快拍数下降或者低信噪比时，二维MUSIC算法中使用的协方差矩阵的特征分解将受到很大的扰动，而特征分解运算对扰动又十分敏感，这就造成估计的均方根误差大，估计值散布大。对比说明本文算法有很强的抗噪性能和稳健性。

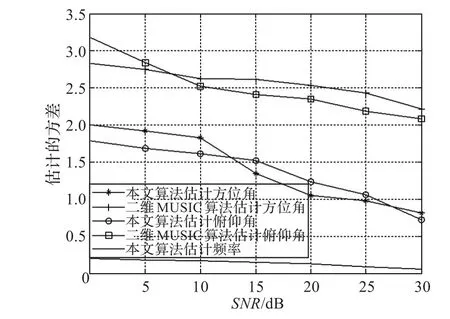
图3 参数估计的方差随信噪比的变化曲线图

图4所示为文献[2]中的算法与本文算法的收敛性能比较。本文算法收敛比文献[2]算法稍慢，但本文算法搜索到了更高的亲和力值，且亲和力值的范围大，这说明文献[2]算法存在“早熟”现象，收敛到了局部最优，并未搜索到全局最优；本文算法搜索范围大，并且逐步收敛到全局最优，这说明本文以式（10）作为亲和力评价函数的可行性，它局部极值点少，包络平坦，能使优化算法发挥更好的性能。

图4 收敛性能比较图

对文献[2]算法、二维MUSIC算法以及本文算法，在信噪比为20 dB的情况下（其余条件不变）进行10次Monte-Carlo仿真实验。表1所示为文献[2]算法与本文算法运行时间的比较结果，可以看出二维MUSIC算法的运行时间最长，文献[2]算法次之。这主要是因为二维MUSIC算法采用全方位逐次搜索，计算量自然大，文献[2]算法和本文算法均是向最优方向有目的的搜索，所以计算量要小，同时本文算法还优于文献[2]算法，这充分体现了本文算法的高效性。

表1 运行时间比较s

6 结论

将量子免疫进化算法与多维参数估计结合起来，有效地拓展了量子进化算法的应用范围，通过理论推导和仿真分析，证明了算法的优越性，避免了特征分解和穷尽搜索等算法存在的稳健性差，运算时间长（穷尽搜索的单次运行时间高达8 200.4 s[1]）等缺点。但本文算法亲和力函数的选择从本质上讲还是属于子空间拟合类算法，怎么样才能寻找到更合理的亲和力函数是一个问题。同时，从图2可以看出二维MUSIC算法方位角和俯仰角估计的误差基本相当，本文算法对两个角度估计的误差虽然都很低，但在低信噪比时却相差很大，这说明二维MUSIC算法对两个角度的估计是互不影响的，而本文算法由于将两个角度的编码放在同一个染色体上所以每一对方位角和俯仰角之间是有影响的。今后，对以上这两个问题将进一步研究。

[1]牛奕龙，陈志菲，孙进才，等.估计声信号二维参数的免疫量子克隆算法[J].数据采集与处理，2010，25（1）：33-38.

[2]栾鹏程，吴瑛.改进遗传算法在DOA搜索中的应用[J].电光与控制，2006，13（3）：65-68.

[3]吴秋逸，焦李成，魏峻，等.量子协同免疫动态优化算法[J].模式识别与人工智能，2009，22（6）：863-868.

[4]Han K H，Kim J H.Quantum-inspired evolutionary algorithms with a new termination，H gate，and two-phase scheme[J]. IEEE Transactions on Evolutionary Computation，2004，8（6）：156-168.

[5]Jiao Licheng，Li Yangyang，Gong Maogou，et al.Quantuminspried immune clonal algorithm for global optimization[J]. IEEE Trans on System，Man and Cybernetics，2008，38（5）：1234-1253.

[6]杨淑媛，焦李成，刘芳.量子进化算法[J].工程数学学报，2006，23（2）：241-246.

[7]张贤达.现代信号处理[M].北京：清华大学出版社，2002：522-524.

[8]High resolution 2-D DOA estimation using second-order partialdifferential of MUSIC spectrum[C]//Proceedings of the IEEE InternationalSymposiumonCircuitsandSystems，2008：1152-1155.

QIU Xinjian1，2,LI Qinghua1,XUE Fengfeng3,PENG Anhong1

1.Intelligent Signal Processing Lab,College of Information Science and Engineering,Xinjiang University,Urumqi 830046,China
2.Unit 68203 of PLA,China
3.Telecommunications Engineering Institute,Air Force Engineering University,Xi’an 710077,China

Using the relationship of the time-equivalent between the array signal processing and the airspace,to based on the plane array,using singular value decomposition and the generalized eigenvalue decomposition of array covariance matrix,the frequency of the

signal can be estimated.A function of antigen and antibody affinity is proposed by analyzing the array model.It can estimate the pitch angle and azimuth signal using the characteristics of the evolution of immune.Thus the multidimensional array signal parameter estimation can be completed.The numerical stability,noise immunity and time consuming of multi-dimensional parameters estimation can be improved.The computer simulation shows that the proposed algorithm is effective. Key words：quantum computation;immune evolutionary algorithm;multi-dimensional parameter estimation;spectrum estimation;space-time signal processing

利用阵列信号处理时域与空域等效的关系，以平面阵为基础，采用阵列协方差矩阵的奇异值分解和广义特征值分解估计接收信号的频率，通过分析阵列模型，提出一种抗原和抗体的亲和力函数；利用量子免疫进化的特性，估计出信号的俯仰角和方位角，从而完成阵列信号的多维参数估计，改善了多维参数估计的抗噪性能、数值稳定性和运行时间。通过计算机仿真，证明了该算法的有效性。

量子计算；免疫进化算法；多维参数估计；谱估计；空时信号处理

A

TP18

10.3778/j.issn.1002-8331.1201-0182

QIU Xinjian,LI Qinghua,XUE Fengfeng,et al.Space-time multi-dimensional estimation using quantum immune evolutionary algorithm.Computer Engineering and Applications,2013,49（19）：210-212.

国家自然科学基金（No.60971130）。

邱新建（1984—），男，博士研究生，主要研究方向智能信号处理，模式识别；李庆华（1987—），女，硕士生；薛凤凤（1986—），女，博士生，讲师；彭安洪（1985—），男，博士生。E-mail：tonggong0412@163.com

2012-01-20

2012-07-19

1002-8331（2013）19-0210-03