非平衡电桥测量磁致伸缩系数

郭敏强，郭启凯，杨 斌，张亚萍，刘彦民，闫向宏

(中国石油大学(华东)理学院，山东 青岛266580)

0 引 言

磁致伸缩材料的磁致伸缩系数是衡量材料本身性质的一项重要指标，目前测量磁致伸缩系数的方法主要有迈克尔逊测量法、光杠杆和机械杠杆组合测量法等［1-2］。迈克尔逊测量法中要注意测量样品和其两端夹件的黏接，虽然该系统灵敏度高，但它所需要的干涉仪是比较精密的光学仪器，比较“娇嫩”，也比较笨重，系统的调节步骤比较严格，对操作者的实验技能要求较高。光杠杆和机械杠杆组合测量法无需专门仪器，由于机械杠杆和光杠杆的复合联动，存在一定的系统误差，而且测量过程中望远镜的对焦不准、视差、仪器的晃动等都会引起读数误差，测量精度不高［1，3］。

针对以上问题，本文介绍了一种新型的非平衡电桥电路测量磁致伸缩系数的实验装置和利用检流计偏转值计算磁致伸缩系数的方法。测量人员只需在检验定标之后直接置材料于磁场中，在相同的磁场间隔内从检流计上读出检流计偏转值α，将其代入本文给出的含有检流计偏转值参数的磁致伸缩系数计算公式即可求得实验结果。该方案克服了以前非平衡电桥操作计算复杂的缺陷，测量步骤简洁快速，操作方便，测量精度高，所用精密仪器少。另外，该电桥装置构成不但可以消除因温度、磁阻效应而产生的漂移等现象的影响，而且具有温度补偿作用。

1 实验原理

1.1 Fe-Ga 合金的磁致伸缩应变机制

Fe-Ga 磁致伸缩材料为体心立方结构，它具有高的磁致伸缩各向异性。Fe-Ga 合金的磁致伸缩应变主要是在磁化过程中非180°畴壁位移或磁矩的转动造成的［4］。磁畴的畴壁位移及磁矩的转动与合金的取向和磁矩有密切关系，Fe-Ga 合金的易磁化方向为〈100〉方向。对于〈110〉轴向取向的多晶合金，当在磁矩取向〈110〉方向施加一磁场时，为了减小静磁能，〈100〉轴向取向合金的磁矩会向〈110〉方向旋转，各个晶粒的磁致伸缩应变都沿〈110〉方向做有序排列，因而Fe-Ga 合金表现出大的磁致伸缩应变［5］。

1.2 应变电阻片测量法

电阻应变片是最常用的测力传感元件，其结构是将金属丝或半导体制成栅(见图1)贴在基底上。当用应变片测试时，应变片要牢固地贴在测试体表面;当测试体受力发生形变时，应变片的敏感栅变形，其电阻随之发生相应的变化。通过测试电路将测试体的形变信息转换成电阻电信号输出显示［6］。由于磁致伸缩形变率正比于电阻变化率，则测量磁场内黏贴电阻应变片样品的磁致伸缩系数λ［7］可表示为

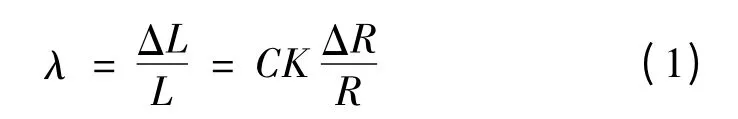
式中:C 为应变电阻片的结构参数;R 为应变电阻片的原阻值;K 为包含测量系统的放大倍数。

图1 电阻应变片传感器

设R20为黏于待测样品上的电阻应变片，当样品的长度发生变化ΔL/L 时，电阻应变片也与之发生一定比例的变化，电阻应变片的阻值变为

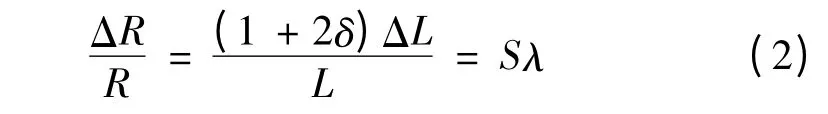
式中，S(S=1 +2δ)为电阻应变片的灵敏系数，由厂家给出。本实验中所用Fe-Ga 磁致伸缩材料，厂家所给的S=2.1。

1.3 实验原理

在非平衡电桥的基础上，用整体代换的思想可改装为如图2 所示的电路，电阻R1和R4为比率臂电阻(取R1∶R4=1 ∶1)，R20为黏贴于待测样品上的应变片电阻(4 个350 Ω 应变片电阻串联);R2、R3为可调电阻箱，桥上为灵敏电流计(电源电压2 ～5 V)。

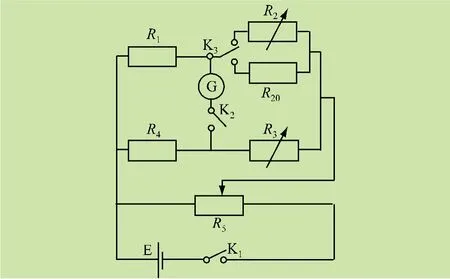
图2 新的电桥实验电路图

在连接电路之前，首先用电流表检验电阻箱阻值变化是否均匀，之后按照图2 连接实验电路［6，8］。闭合开关K1、K2，将K3置于R20，调节R3使得检流计示数为零，记录下此时R3的阻值(即所测得所贴应变片R20的阻值)。将开关K3置于R2，调节R2使得检流计示数为零，并以此时为基准，逐次向同一个方向调节R2，并记录R2阻值和对应的检流计示数α，作ΔR2/R2－α 关系曲线。若此时关系曲线线性程度好，则可运用非平衡电桥原理实现高精度测量。

调节R2使检流计示数为零(即回到基准状态)，将K3置于R20，R20置于激励磁场中，逐渐增加激励电流(产生激励磁场)，同时记录不同时刻检流计的示数和激励磁场的大小，即可得出λ 与磁感应强度B 的关系曲线。

1.4 非平衡电桥法测量λ 原理

连接好电路，改变R2，使之阻值变化量为ΔR2，由此引起的检流计偏转值为α。桥臂阻值相对变化量ΔR2/R2与α 间为线性关系，可先确定ΔR2/R2与α 的比例系数k，即有

假设R2与R20并联，R'2、α'为调节过程中每一时刻的值，R2为R'2与R20并联的总电阻值，其他部分不变，有

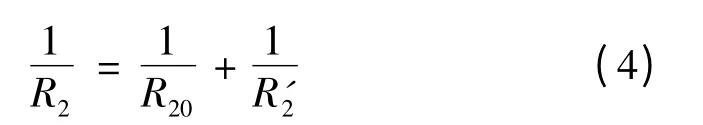
则由式(4)可得

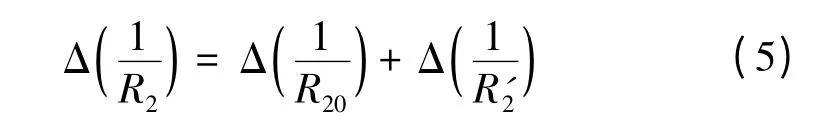
简化上式，则约有

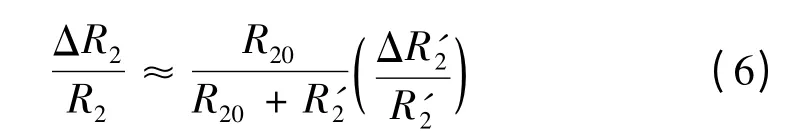
式中:R2指桥路达到稳定时的值;ΔR2指桥路偏离原来状态时R2的变化量。

由式(3)、(6)推知

则由式(2)、(7)可得

实验中通过作出(ΔR2/R2)－α 关系曲线，用图解法来确定k。之后将待测样品和补偿应变片置入磁场内，改变磁场，待测样品发生长度变化，导致ΔR2/R2变化，检流计偏转，最终由α 可确定待测样品的λ。

1.5 平衡电桥法测量λ 原理

利用电阻应变片的应变效应，通过平衡电桥进行实验［8］，测定λ。实验装置仍如图2 所示，只是将R20与可变电阻R2并联。之后，通过外加磁场对磁致伸缩材料励磁(磁场大小由输入线圈的电流控制)，调节R3使检流计示值为零，R3所示阻值即为R2，如此重复获取多组数据并记录［9］。电阻R2，R20臂的总电阻变化值ΔR 为

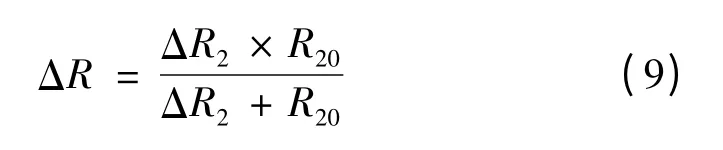
由式(2)得

2 实验结果与讨论

2.1 非平衡电桥法实验结果及分析

图3 为励磁电流与磁感应强度关系曲线图，在逐步调节励磁电流的过程中它们之间呈线性均匀变化，其线性拟合关系式为

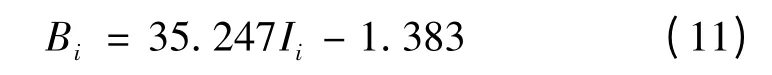
式中，Bi、Ii为调节过程中的瞬时值。由此表明实验过程中励磁电流与磁感应强度稳定变化的线性关系。实验中可通过间接测量电流的大小来获取磁场值，避免了实验中所用特斯拉计测量范围的限制和单次测量所带来的误差，获取较大范围较精确的磁场数据。

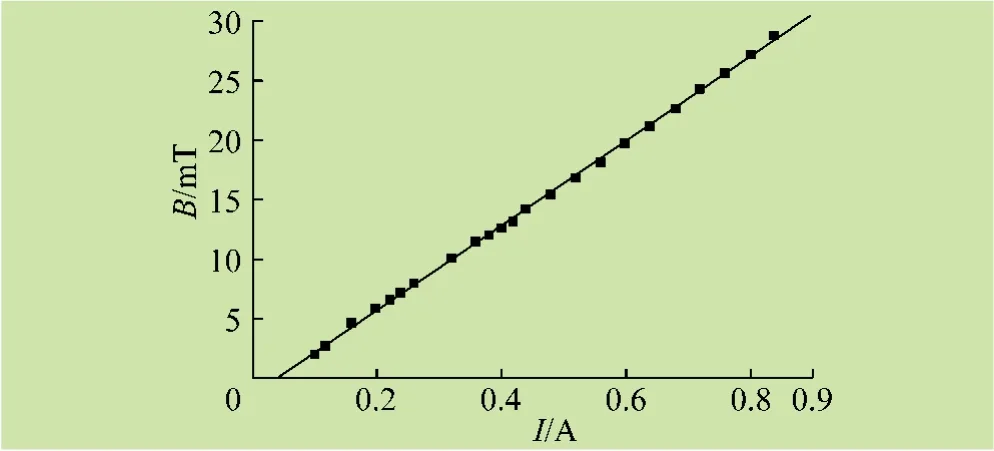
图3 励磁电流与磁感应强度关系曲线

图4 为检流计示值α 与阻变ΔR2/R2关系曲线图，其线性拟合关系式为

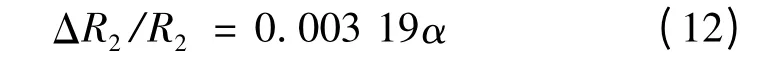
从而确定出本实验条件下k =0.003 19，ΔR2/R2与摆角α 变化关系符合非平衡电桥法测量的原理，能够用于实现λ 的测量。

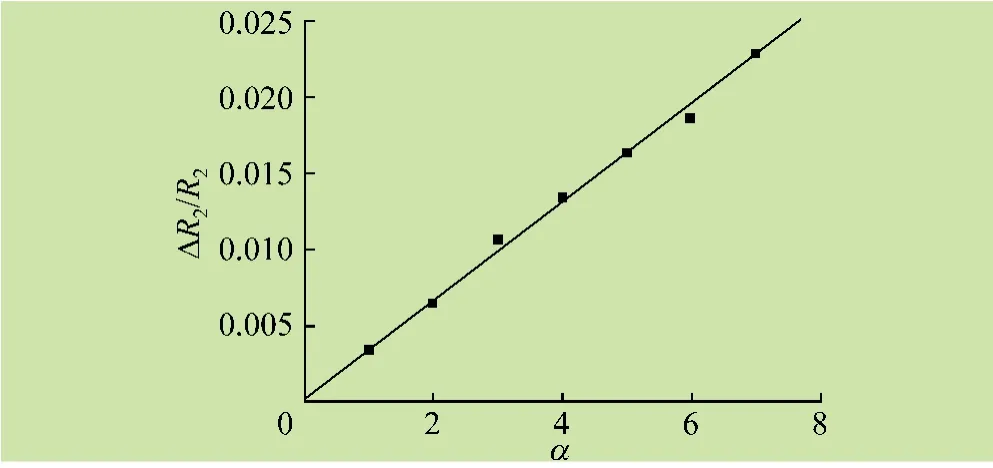
图4 检流计示值α 与阻变ΔR2/R2 关系曲线

图5 为磁感应强度B 与Fe-Ga 合金材料λ ×10－6的关系曲线，曲线图过渡相对比较稳定，避免了突变现象的出现，减小了误差，较真实地反映出了材料在不同磁场下的变化情况，达到了预期效果。

在激励磁场条件下，微观上为了减小各个晶粒的静磁能，非180°畴壁产生位移或磁矩发生转动，向易磁化方向转动，各个晶粒的磁致伸缩应变都沿易磁化方向做有序排列，因而Fe-Ga 合金表现出大的磁致伸缩应变;宏观上表现出磁致伸缩材料长度伸缩，不同样品在不同的磁场强度范围，材料伸缩量不同，因此不同磁致伸缩材料会有不同的磁致伸缩曲线。

图5 的磁致伸缩曲线反映出Fe-Ga 合金磁致伸缩材料在磁场中λ 随磁场变化的特点。在起始时，随着磁场的增加，λ 增幅较大;在大约10 mT 之后，随着磁场增强，λ 的增幅变小，从一定程度上说明了这种Fe-Ga 合金磁致伸缩材料的伸缩性能在低磁场条件下比较好。当磁场强度较强时，λ 的增幅减小是由于分子之间的相互作用力引起的。对曲线进行拟合所得关系式为

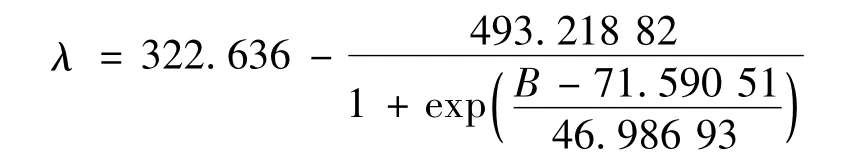
所拟合出的曲线从量化的角度反映出这种Fe-Ga合金磁致伸缩材料的性能。

2.2 平衡电桥法实验结果及分析

图6 为平衡电桥电路下磁感应强度B 与λ 的关系曲线，其变化趋势和非平衡电桥的变化相似，微观和宏观机理也与非平衡电桥的相同，其多项式曲线拟合所得关系式为

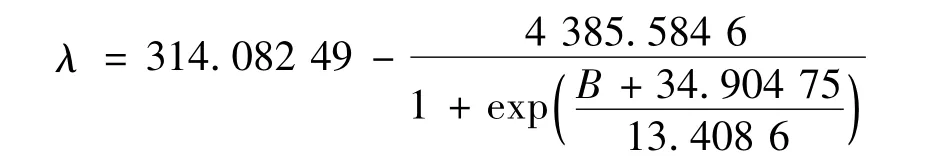
表明了Fe-Ga 合金磁致伸缩材料在磁场中λ 随磁场变化的特点与非平衡电桥的大致相似，但曲线出现了较小的波动，这是因为平衡电桥电路调节过程中旋钮的接触电阻以及电阻箱本身误差和电阻调节变化不均匀现象的存在，致使偶然性和不确定因素增大。

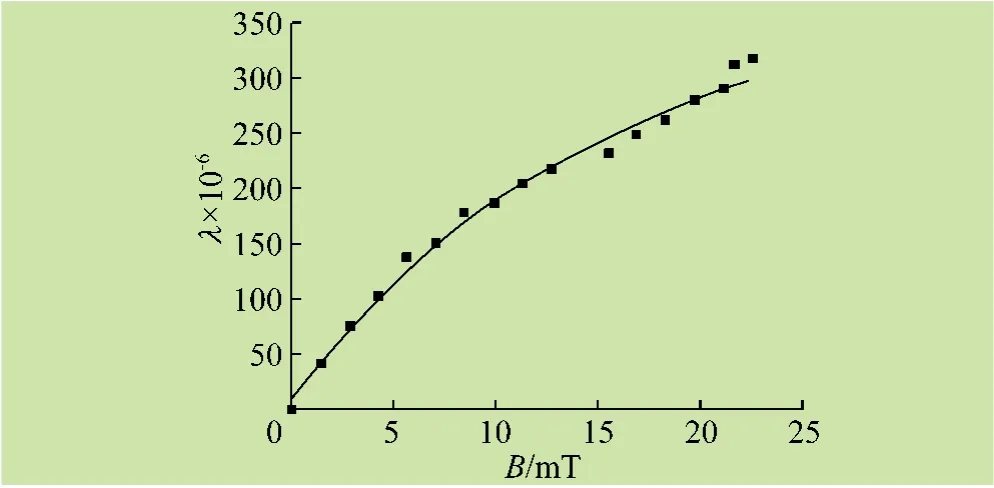
图6 磁感应强度B 与λ 的关系曲线(平衡电桥)

2.3 综合比较分析

将图5、6 进行比对，可看出新装置所得出的实验结果曲线更加稳定平滑，少了很多偶然因素的影响。在2 个实验中所用的应变片的个数相同，所用激励磁场大小也相同，但所得出的2 个曲线并不能完全吻合。其原因:①电桥的不同连接方法对此产生较大影响，所表现出的结果会有些差距;②由于平衡电桥在调节过程中需要多次调节不同档次状态平衡，不仅增加了调节的次数，也使得单次调节中的偶然误差增大，所测数据的准确性变差;③虽然使用精度较高的直流复射式检流计，但它的光标是向两个方向摆动的，仍然避免不了出现一定的滞后效应，也就显示出如平衡电桥法所测得的数据会在拟合曲线两侧波动较大;④由于每次调节时电阻箱接触电阻产生的影响和温度、磁阻效应产生的漂移等现象的影响，使得测量误差加大。

用新装置测量，在磁致伸缩棒上所黏贴的4 个电阻应变片在磁场中可进行温度补偿，消除因为温度、磁阻效应产生的漂移现象的影响;实验仍采用直流复射式检流计，但在原理上运用了整体代换的方法，先进行定标获取k 值，由于可以获取大量的实验数据，对测量范围的限制较小，因此定标比较准确;实验中所用的直流复射式检流计和电桥结构本身使得测量精度大大提升;将所测样品置于可变磁场中，只需调节磁场大小，不用调节电阻，检流计光标会一直向一个方向偏转，避免了平衡电桥中光标来回摆动的现象、光标滞后效应、单次调节误差和接触电阻等产生的误差。

3 结 论

介绍了新型的测量磁致伸缩材料磁致伸缩系数的实验装置，通过对非平衡电桥法和平衡电桥法的实验结果进行系统、综合比较，得出以下结论:

(1)该电桥测量系统的灵敏度主要取决于应变片的结构参数以及个数、电桥接法和所用检流计的精度;

(2)新型实验装置和磁致伸缩系数的测定方法具有较强的可行性，不但解决了传统的磁致伸缩材料磁致伸缩系数测量过程中存在的读取误差大、操作难、费用大、单次测量引入随机误差的可能性大等诸多问题，而且将长度测量转化成电阻和检流计偏转值的测量;

(3)从传统的磁致伸缩系数计算公式出发，结合整体代换的方法，给出了简易可用的含有检流计偏转值参数的磁致伸缩系数计算公式，为从量化角度把握样品材料的性能提供了依据。

Fe-Ga 合金具有良好的延展性，可热轧，抗拉强度较高，很好的温度特性，及能够在较宽的温度范围内使用［10-11］，在重要的能量与信息转换功能材料、换能器技术、海洋探测技术、微位移致动、智能机翼、机器人等高技术领域具有广泛的应用前景。同时，它是新世纪提高国家竞争力的战略性功能材料［12-13］。新装置和新方法测量磁致伸缩系数简单、实验时间短、精度好、操作方便，且测量结果与实际值符合度高，不仅适用于科研工作中的磁性测量，还可以应用于高校理工类学生的物理教学，在进一步实现数据的自动化采集和处理上具有较大优势，适合工业上高精度的磁致伸缩系数测量［13-15］。因此，深入精确研究磁致伸缩材料磁致伸缩系数具有重要意义。

［1］ 张永炬，林朝斌.磁致伸缩系数试验测定方法的比较［J］.台州学院学报，2000，25(3):49-51.

［2］ 张光睿，江丽萍，吴双霞，等. Fe-Ga 合金磁致伸缩性能的研究进展［J］.材料研究与应用，2010，4(1):5-8.

［3］ 杨 兴，贾振元，郭东明.超磁致伸缩材料的伸缩特性及其磁感应强度控制原理及方法的实现［J］.电工技术学报，2001，16(5):55-58.

［4］ 韩志勇.Fe83Ga17微分磁致伸缩系数和各向异性常数的研究［J］.中国民航大学学报，2007，25:135-136.

［5］ Kellogg R A.Development and modeling of rion gallium alloys［D］.Iowa State University，2003:156.

［6］ 李 蓉.基础物理实验教程［M］. 北京:北京师范大学出版社，2008(4):298-300.

［7］ 佟荣光，赵建林.成振龙等磁致伸缩材料弱磁场响应特性的实验研究［J］.光子学报，2009，38(2):311-314.

［8］ 李书光，王殿生. 物理实验教程［M］. 东营:中国石油大学出版社，2006(10):90-95，103-113.

［9］ 汪逸新，闰专怀. 载波电桥法测磁致伸缩系数［J］. 物理实验，1995，16:148-150.

［10］ GURUSWAM Y S，SRISUKIUMBOWOMCH AI N，CLARK A E，et al.Strong duct ile and low field magne tostrictive alloys based on Fe-Ga［J］.Scripta Mater，2000，43:239.

［11］ KELLOGG R A，FLATAU A B，CLARK A E，et al.Temperature and stress dependencies of the mag netic andmagnetostrictive properties of Fe81Ga19［J］.Journal of Applied Physics，2002，91:7821.

［12］ 高 峰.超磁致伸缩材料特性测量的实验设计［J］. 武汉理工大学学报，2010(6):410-412.

［13］ 韩志勇.Fe83Ga17合金磁致伸缩性能的研究［J］. 磁性材料及器件，2007(10):19-21.

［14］ 唐兴龄，陶 华，司朝润，等.轴向开槽对改善超磁致伸缩材料线性度影响的研究［J］.西北工业大学学报，2010，28(4):559-563.

［15］ 伍艮常. 磁致伸缩式液位传感器［J］. 仪表技术与传感器，2007(12):9-12.