两种光伏MPPT的算法及仿真实验
潘东昱, 张自强, 董 燕
(1.上海师范大学信息与机电工程学院,上海201418;2.阿克苏职业技术学院,新疆阿克苏843000)
0 引言
我国有丰富的太阳能资源,2/3以上国土面积的年总日照量超过5 GJ/m2,年平均日照超过2 200 h,具有开发利用太阳能的有利条件。光伏发电系统是将太阳能转换成电能的发电系统,光伏电池阵列是其中重要组成部分。因此,进行光伏电池最大功率点跟踪的研究与开发,达到充分利用太阳能的目的,对于改善我国的能源结构,实现可持续发展是具有重大的现实意义[1]。光伏阵列最大功率点跟踪(Maximum Power Point Tracking,MPPT)是光伏系统中一个不可缺少的组成部分,其目的是使光伏阵列始终输出最大的功率。这对于提高系统的整体效率有极其重要的作用[2]。目前,最大功率点跟踪算法主要有电压回授法、功率回授法、直线近似法、实际测量法、扰动观察法和增量电导法等。
本文首先针对传统的扰动观察法提出了一种改进型占空比扰动法,然后着重研究了性能更优越的模糊控制法。然后分别建立控制模型,采用 Matlab/Simulink对系统主电路及控制系统进行整体仿真,并在最后分析仿真与实验结果。对比占空比扰动法,使用基于模糊的最大功率点跟踪控制器,保证系统能够根据功率变化的幅度自动调节占空比,在不干扰系统正常工作的情况下,更迅速地感知外界的环境变化,找到最大功率点。
1 系统结构
系统结构如图1所示。其主要部分包括:①光伏电池阵列PV;② DC/DC转换器;③ 数字信号处理器DSP;④电压、电流检测电路;⑤驱动电路。由于光伏阵列的输出电压通常较低,所以DC/DC转换器采用BOOST斩波电路,可使输出电压升高,从而满足负载电压要求或者为后级逆变电路提供足够高的直流电压。通过对光伏电池输出电压Upv、电流Ipv的检测,利用以DSP为核心的控制电路实现MPPT控制算法,由输出占空比d计算脉冲宽度,可以达到最大功率点跟踪。
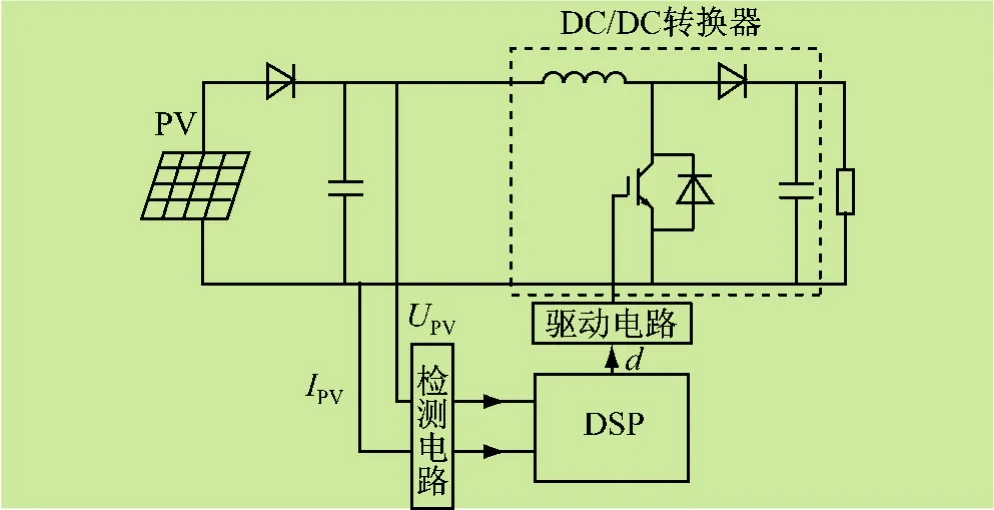
图1 系统结构图
2 光伏阵列的模型和特性
2.1 典型的光伏电池特性曲线
图2是在相同温度不同日照下的太阳能电池P—U特性曲线。从图上可以看出输出功率在某一点达到最大值,该点即太阳能电池的最大功率点(Maximum Power Point,MPP),并随着外界环境的变化而变化[3]。同理在相同光照不同温度下,太阳能电池的输出功率也存在最大功率点。如果太阳能电池采用MPPT控制,就能跟踪不同光强温度下的最大功率,可以最大限度地提高光伏电池的能量利用率[4]。
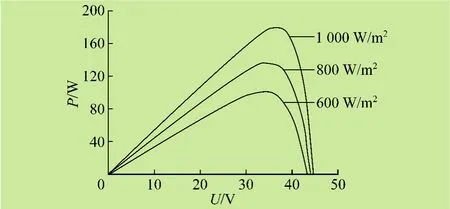
图2 相同温度不同光照的P—U曲线
2.2 光伏阵列的数学模型
由实验测得光伏阵列终端特性,得到实际使用的等效电路如图3所示。图中,二极管D表示一个P—N结对二极管。
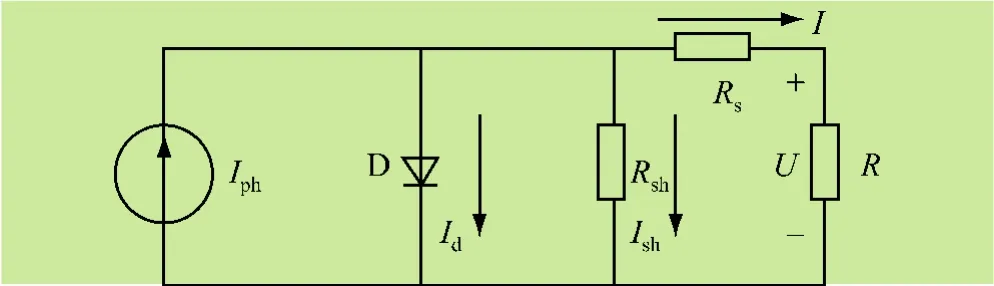
图3 光伏电池等效电路
光伏电池的输出电流、电压关系如下所示:
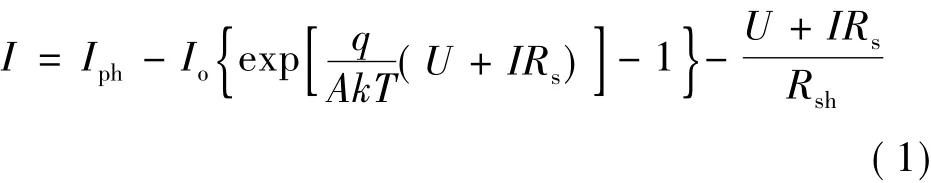
式中:电流源Iph表示光伏电池经由光照射后所产生的电流;Rsh和Rs分别表示材料内部等效的并联及串联电阻;I与U表示光伏电池输出电流及电压;Io表示光伏阵列反向饱和电流(对光伏阵列而言,其数量级为10-4A),q为电子电荷(1.6 ×10-19C);k为波尔兹曼常数(1.38×10-23J/K);T为绝对温度。在下面的讨论中将忽略Rsh,得到简化的光伏电池输出特性方程如下:
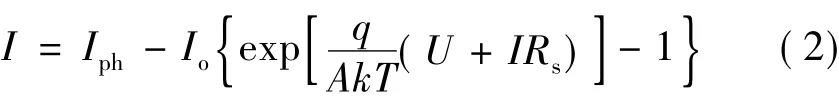
式中:
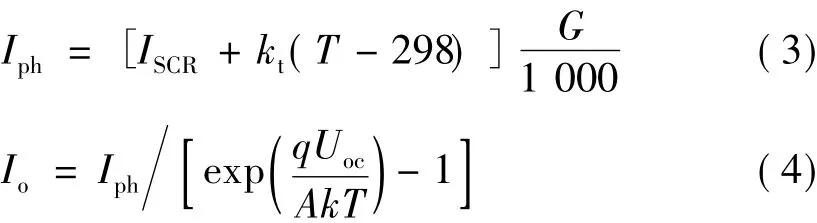
式中:ISCR为标准测试条件下的光伏电池的短路电流;kt为短路电流温度系数。
光伏电池的输出具有明显的非线性。在外部负载短路情况下即U=0,此时光电流Iph全部流向外部的短路负载,短路电流ISCR几乎等于光电流,有ISCR=Iph;在处于开路状态时,I=0,光电流全部流经二极管D,开路电压为
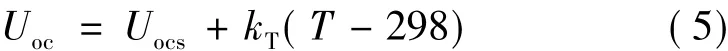
式中:Uocs为标准测试条件下的开路电压;kT为开路电压的温度系数。
3 MPPT算法及建模
在光伏发电系统中,影响MPPT控制效果的关键因素是最大功率点的跟踪速度与精度,而系统调节步长的大小直接影响到这两个要素的质量。当系统的工作点远离最大功率点的时候必须加大调节步长,以加快系统的跟踪速度;当工作点位于最大功率点附近的时候,必须适当减小调节步长,以避免系统在最大功率附近来回振荡,从而确保在达到系统跟踪精度的同时具备良好的稳定性[5]。
本文着重讨论利用占空比扰动法和模糊控制法实现光伏阵列MPPT的具体方法,通过仿真比较两种算法的动态和稳态性能,首先根据光伏阵列的数学模型建立Matlab仿真模型,然后根据Boost电路对阻抗变换规律建立一个DC-DC变换电路的子模块嵌入仿真模型中[6]。
3.1 占空比扰动法
3.1.1 占空比扰动法的原理
传统的扰动观察法的原理是先让光伏阵列工作在某一参考电压下,检测输出功率,在此工作电压基础上加一正向电压扰动量,检测其输出功率的变化。若输出功率增加,表明光伏阵列最大功率点电压高于当前工作点,需要继续增加正向扰动;若所测输出功率降低,则最大功率点电压低于当前工作点,需要反向扰动工作点电压[7-8]。
在文献[9]中对比传统的扰动观察法提出了一种占空比扰动法,通过当前功率与前一时刻功率比较,决定下一时刻直流变换器的占空比D是增加或减小。输出功率P与D之间的关系如图4所示,当d P/d D=0时,输出功率达到最大值。这种方法是直接把占空比D作为控制参数,只需要一个控制循环,从而减小了控制器设计的复杂度。
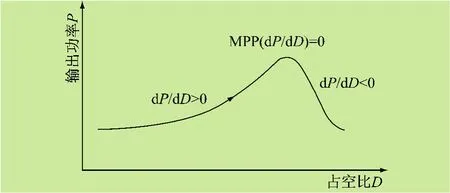
图4 P—D关系的示意图
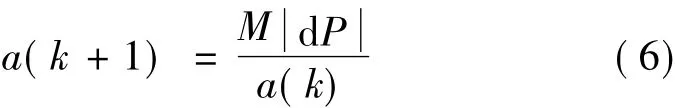
式中:a(k)为占空比D的调整步长,在0和1之间变化;d P=P(k)-P(k-1),表示功率的变化大小;M为一常数。
3.1.2 占空比扰动法建模
利用占空比扰动法建立最大功率点跟踪算法的仿真系统,如图5所示。其中PV模块为光伏电池模块,MPPT控制算法由M文件编写的S函数中实现,分别编写了改进的具有在线参数调整功能的自适应扰动算法MPPT.m,S函数的输入信号为光伏电池当前输出功率P(k)与前一时刻功率P(k-1)之差,输出信号为经MPPT运算得到得占空比D(k)。Transport Delay模块实现输出功率P一个采样周期的延迟[10]。
3.2 模糊控制法
3.2.1 模糊控制法的基本原理
取目标函数为光伏电池的输出功率,控制量为用来控制开关管的PWM信号的占空比D。模糊自寻优在扰动观察法中,调整占空比D时还存在调整步长大小的选择问题:若步长过小,跟踪时间会拉长而影响系统的动态响应特性;若步长过大,输出功率波动加大,其平均值大大小于最大值,则稳态误差变大。通过加入步长a的自动在线调整器(式(6))得到了解决,同时保证了系统的动态和稳态性能。控制器以光伏阵列第n时刻的功率变化量和第n-1时刻的占空比调整步长值为第n时刻的输入量,以光伏阵列第n时刻的占空比调整步长值为第n时刻的输出量。将语言变量E和A分别定义为8个和6个模糊子集,即
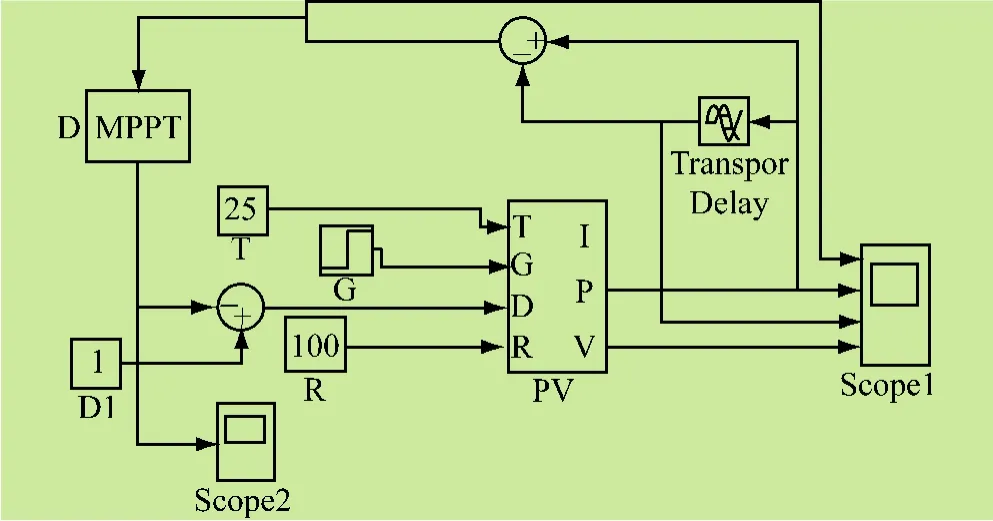
图5 占空比扰动法MPPT仿真系统图

其中 NB,NM,NS,NO,PO,PS,PM,PB 分别表示负大,负中,负小,负零,正零,正小,正中,正大等模糊概念。将它们的论域规定为14个和12个等级,即E={-6,-5,-4,-3,-2,-1,-0,+0,+1,+2,+3,+4,+5,+6};A={-6,-5,-4,-3,-2,-1,+1,+2,+3,+4,+5,+6}[11]。
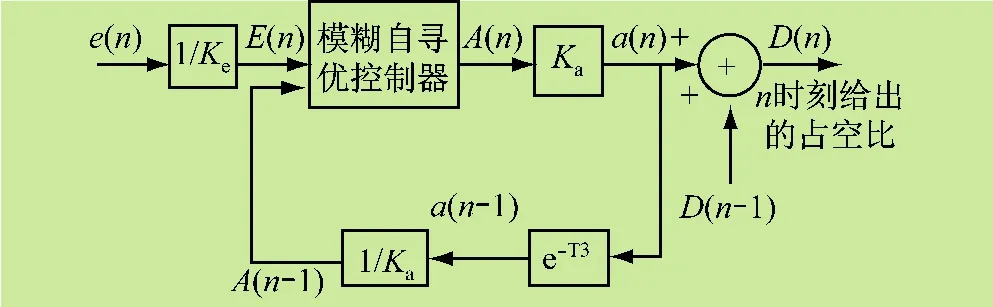
图6 光伏系统模糊控制原理图
根据光伏系统的特点,选择三角形作为隶属度函数的形状[12],功率差E和占空比步长A(n-1)的隶属度函数如图7、图8所示:
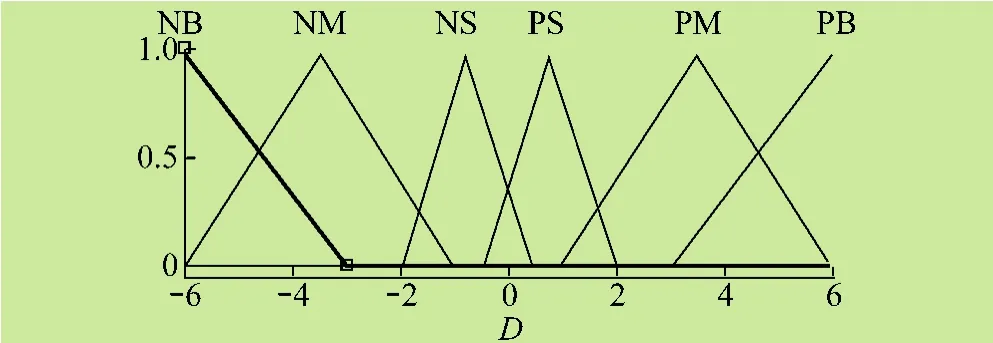
图7 占空比步长隶属度函数
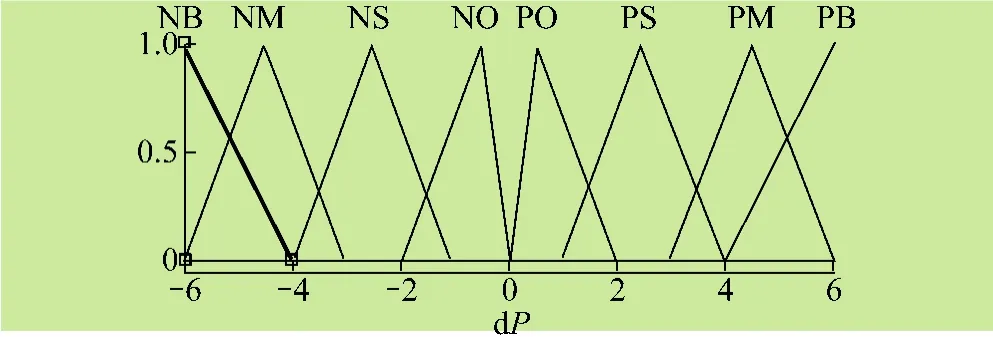
图8 功率差隶属度函数
分析独立发电系统输出功率P与占空比D之间的关系曲线,并根据E和A(n-1)的状态确定步长变化值,使其功率靠近最大点,制定模糊规则如表1所示。
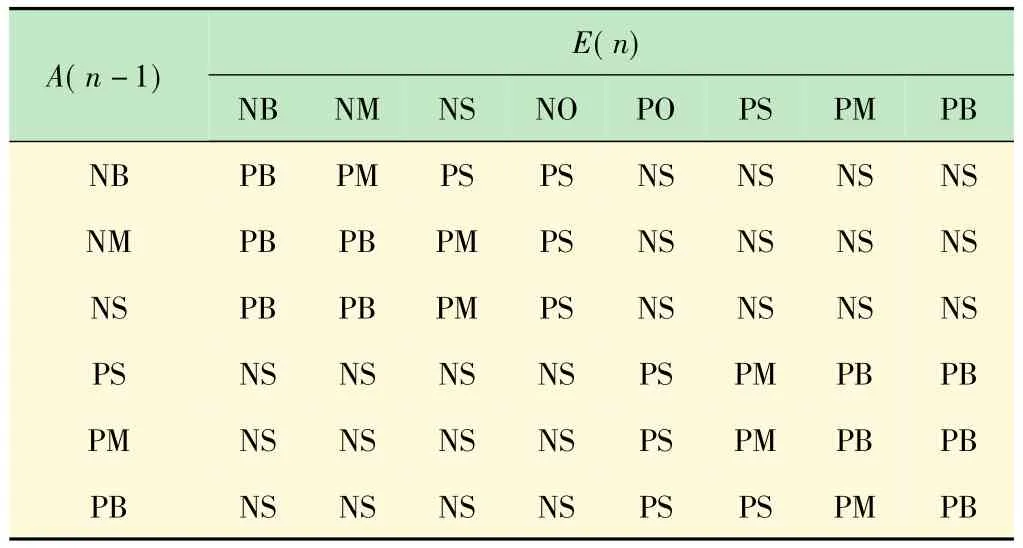
表1 模糊控制的规则
3.2.2 模糊控制法建模
在模糊控制编辑器中,模糊决策选择成熟且容易实现的Mamdani推理算法,“交”方法为min,“并”方法为max,推理方法为min,聚类方法为max,解模糊方法[13]选择具有较高精度的(centroid)。
通过以上完成模糊控制器的设计,进行保存记为fuzzy1。根据光伏阵列的数学模型,通过 Matlab/Simulink建立MPPT模糊控制系统图[14]。其中PV模块为光伏电池模块,两个单位延迟模块分别实现输出功率P、占空比D一个采样周期的延迟,然后对相关参数进行适当的设置[15]。
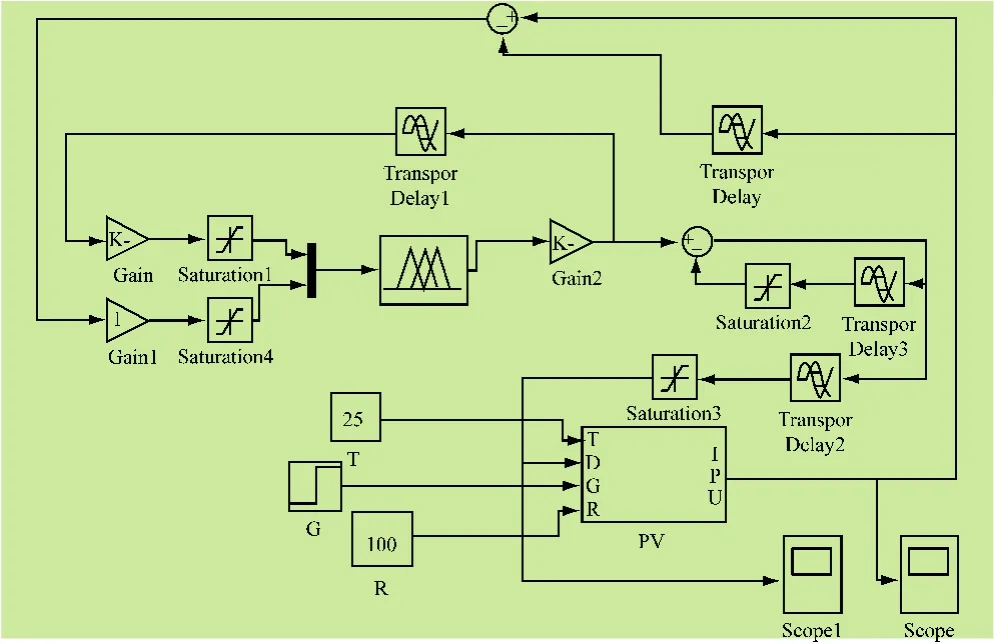
图9 MPPT模糊控制器仿真系统图
4 仿真实验结果分析
光伏电池的额定功率为100 W,光伏阵列的开路电压为21.7 V。短路电流为4.8 A,采样频率为20 kHz,设置仿真外界因素日照强度从600 W/m2突然增大到1 000 W/m2,光伏电池表面温度T=25℃,负载阻值R=100Ω。以下采用占空比扰动法和模糊控制两种算法进行仿真对比。
对于占空比扰动法采用变步长ode 45,设置仿真时间为1 s,扰动步长为0.000 2。运行仿真后就可通过scope观察系统的仿真输出结果。如图10和图11所示,MPPT跟踪速度较快,动态响应性能较好,但到达稳态后有微小的波动。
对于模糊控制法采用Fix-step Discrete,步长是0.000 2,运行仿真后就可通过scope观察系统的仿真输出结果,如图12和图13所示。相比于占空比扰动法,模糊控制器的控制使光伏电池模块更迅速平稳地跟踪到最大功率点,在最大功率从点几乎没有波动,减小了由于振荡而引起的功率损耗,当外界环境变化时,如图12所示在0.5 s时迅速地跟踪到新的最大功率点,没有发生误判,稳态也没有震荡,表现出良好的动态和稳态性能。参数的计算方法也没有前述的改进的自适应占空比扰动法那么繁琐。反复调整参数得出仿真输出结果如图10~12所示。
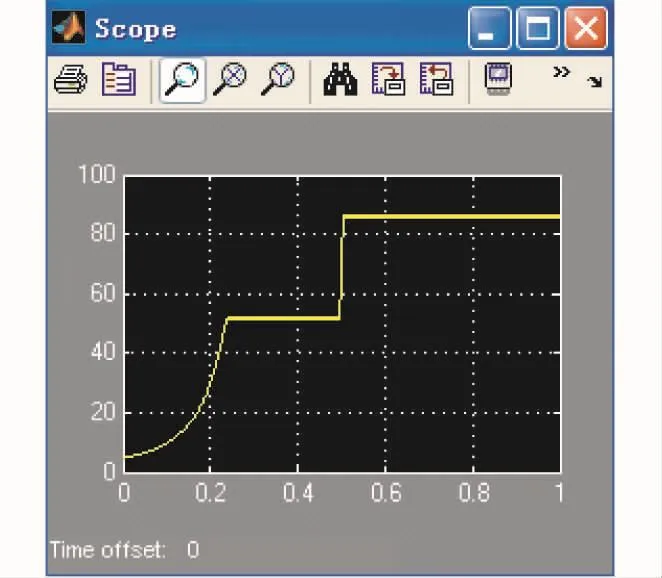
图10 功率输出(采用占空比扰动控制)
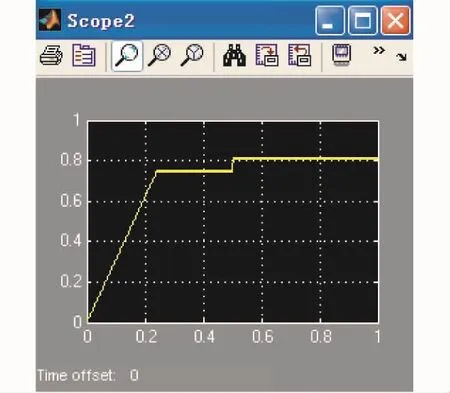
图11 占空比输出(采用占空比扰动控制)

图12 功率输出(采用模糊控制)
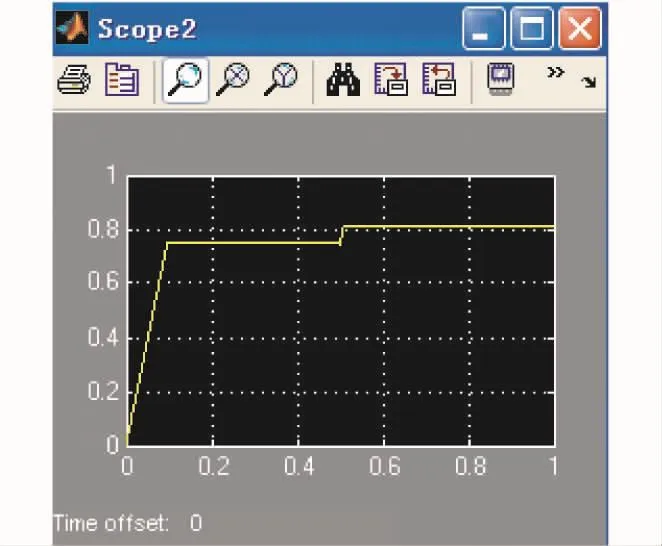
图13 占空比输出(采用模糊控制)
5 结语
对光伏发电系统进行建模分析,直接将占空比步长作为控制变量,采用占空比扰动法和模糊控制法,根据光伏功率变化的幅度对占空比进行自适应调节,对比两种控制算法的仿真结果,验证了模糊控制方法在快速跟踪最大功率点的同时,也具有非常小的稳态功率波动的优点。实验证明将模糊逻辑技术应用于最大功率点跟踪控制,相较于占空比扰动法具有更好的动态性能和稳定性。
[1] 叶秋香.光伏电池最大功率跟踪器的模糊控制及其应用研究[D].上海:东华大学,2006.
[2] 赵争鸣.太阳能光伏发电及其应用[M].北京:科学出版社,2005.
[3] 靳瑞敏.太阳能电池原理与应用[M].北京:北京大学出版社,2011.
[4] 滨川圭弘.太阳能光伏电池及其应用[M].北京:科学出版社,2008.
[5] 黄克亚.光伏电池最大功率点跟踪算法研究及实现[D].兰州:兰州大学,2010.
[6] 张德丰.Matlab自动控制系统设计[M].北京:机械工业出版社,2010.
[7] 赵争鸣,刘建政,孙晓瑛,等.太阳能光伏发电及其应用[M].北京:科学出版社,2005.
[8] 吴理博,光伏并网逆变系统综合控制策略研究及实现[D]北京:清华大学,2006.
[9] WEIDONG XIAO,DUNFORD W G.A modified adaptive hill climbing MPPT Method for photovoltaic power systems[C]∥35th annual IEEE power electronics specialists’conferences,germany,2004,1957-1963.
[10] 于 群,曹 娜.Matlab/Simulink电力系统建模与仿真[M].北京:机械工业出版社,2011.
[11] 席爱民.模糊控制技术[M].西安:西安电子科技大学出版社,2008.
[12] 石辛民,郝整清.模糊控制及其Matlab仿真[M].北京:清华大学出版社,2008.
[13] Chung-Yuen Won, Duk-Heon Kim, Sei-Chan Kim. A new maximum power point tracker of Photovoltaic arrays using fuzzy controller[J].IEEE Translnd Electron,2004(3):396-403.
[14] 张德丰.Matlab自动控制系统设计[M].北京:机械工业出版社,2010.
[15] 张 静.Matlab在控制系统中的应用[M].北京:电子工业出版社,2007.

