电网连锁故障预防的多阶段序贯博弈模型

常辉 刘树伟 朱旭凯 张艳 徐得超 徐树文

1中国民航机场建设集团公司规划设计总院，北京 朝阳 100101

2中国电力科学研究院，北京 海淀 100053

1 引言

近年来，国内外电力系统发生过多次大规模连锁故障导致的大停电事故[1]，如何有效地防止电力系统连锁故障是避免大停电事故的关键，这一问题成为当前的研究热点。现有的研究方法尚未很好解决连锁故障预防问题，这一问题也是当前的研究难点。

博弈理论应用于电力系统的研究主要集中于电力市场方向，其在社会学、经济学、管理学、政治学、军事学等领域[2-3]，将博弈理论用于电网连锁故障及大停电的预防尚属首次。

序贯博弈是博弈方按照先后次序采取策略或行动的一类博弈。电网产生故障或其他扰动后，电网调度运行人员需根据电网的实际情况做出调整以保证电网持续可靠运行。实际电网发生连锁故障时，伴随着电网扰动（或故障）与调度运行人员对电网调整（有的时候这种调整可能恶化系统运行）的交替，若假定电网调整都是正确的，且电网的扰动也是具有理性的，则电网预防连锁故障的过程表现为“扰动方”（定义为A方）与“防御方”（定义为B方）的攻防博弈。

2 连锁故障多阶段序贯博弈描述

2.1 几个假定

⑴“理性”的不对称假设：具有完全理性的A方总是试图采取最能威胁B方的一个或多个行动，实际电网中电网的扰动有的时候是随机的，因此A方具有有限理性更符合实际，也就是说A方清楚本方的目标与利益，但不知道哪些行动是具有威胁的，其收益是系统损失负荷，其目标是电网发生连锁故障；而B方行动具有针对性，因此假定具有完全理性；

⑵“可观察行动”的不对称假设：博弈方B完全了解电网中的情况，即在决策时清楚电网中发生的扰动事件；而A并不关心B的任何行动和信息；

⑶博弈方A的收益定义为增加系统负荷的损失，这个值总是大于等于零的；博弈方B的收益定义为减少系统负荷的损失，该值总是小于等于零。二者完全对立；

⑷实际电网中A与B的行动往往是非同时的，这里也假定二者交替而不同时。

2.2 连锁故障博弈树

对于连锁故障的博弈过程可采用博弈树的方式来描述。连锁故障博弈方的决策点定义为结；示博弈方可能采取的行动定义为枝，两个结之间通过枝来链接，博弈的结果成为末端结。

图1为具有两个阶段博弈过程的连锁故障描述。这里初始结为a，末端结为f、g、h、i。在结a处标有字母“A”，表示博弈方A在此处决策（B方不决策），同样结b、c上标字母“B”,表示B方决策（A方不决策），在两个结之间的枝都标有行动，在末端结标有博弈双方的收益。连锁故障博弈的一个局势可为从开始结到终止结的任一路径。

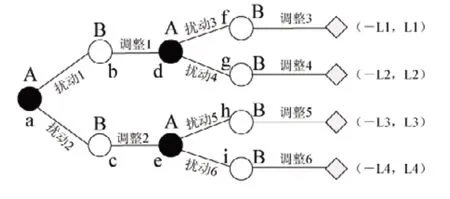
图1 二阶段连锁故障博弈例Fig.1 Example of two-phase cascading failure game

连锁故障博弈树能够清晰的描述博弈双方序贯博弈的过程，表现形式十分形象、清晰。

3 连锁故障多阶段序贯博弈模型与目标函数

3.1 博弈模型

按照上述博弈双方交替序贯博弈过程，可建立预防连锁故障的多阶段序贯博弈模型，该模型可采用图2进行描述。在该模型中，博弈方A的行动按照不同的方法进行分类，例如按照故障元件可分为保护误动、线路故障、发电机故障等；博弈方B的行动可按照不同的关注角度进行分类，例如考虑A方行动可能产生的功角稳定问题。

图2 连锁故障多阶段序贯博弈模型Fig.2 Multi-stage sequential-move game model for Cascading failure

图2中的模型中，在某一阶段的博弈过程中，博弈方B选择行动时，应考虑下一阶段博弈方A的可能行动，进而防止博弈方A下一阶段的行动导致系统出现博弈方B来不及调整的情况。进入下一阶段博弈，博弈方A采取行动后，博弈方B继续调整，如此反复，形成多阶段序贯博弈。

3.2 目标函数

连锁故障预防的目标是以最少的负荷损失作为控制代价确保系统不发生连锁故障，预防电网大面积停电。目标函数定义为：

式中，R为可调整负荷节点集合， 表示在序贯博弈第j阶段在可调整负荷点i的调整值，K为序贯博弈的阶段序号。

目标函数最小化的同时，博弈方B的收益函数达到最大化，同时博弈方A收益函数最小化。

4 结语

世界范围内发生的大停电事故有一个共同特征：包含连锁故障阶段。本文构建了预防电网连锁故障多阶段序贯博弈模型，对于防止电网大规模停电具有重要意义。基于该模型，结合连锁故障多集中在初始故障附近区域的特点，赋予博弈方A一定理性，可使模型计算量大大降低，提高计算效率。

[1]电网技术编辑部．进入新世纪世界各地频发大范围停电事故[J]．电网技术，2005，29(11)：84．

[2]Thmas L C. Games-theory and applications(M). Ellis, Horwood Limited, 1984.

[3]Osbome M J, Rubinstein A. A course in game theory[M]. The MIT Press, 1994, 277-298.