A New Algorithm for TSP Using Hopfield Neural Network with Continuous Hysteresis Neurons

ZHANG Wei

(Mathematics,Physics and Information Science School of Zhejiang Ocean University,Zhoushan 316004,China)

1 Intorduction

The auto associative memory model proposed by HOPFIELD[1-2]has attracted considerable interest both as a content address memory(CAM)and,more interestingly,as a method of solving difficult optimization problems[3-5].The Hopfield neural network contain highly interconnected nonlinear processing elements(“neurons”)with two-state threshold neurons[1]or graded response neurons[2].TAKEFUJI and LEE[6]proposed a two-state(binary)hysteretic neuron model to suppress the oscillatory behaviors of neural dynamics.However,TATESHI AND TAMURA[7]showed TAKEFUJI and LEE’s model did not always guarantee the descent of energy function,WANG[8]also explained why the model may lead to inaccurate results and oscillatory behaviors in the convergence process.Since their report,several modifications on the hysteretic function,for example GALÁN and MUÑOZ’s[9]binary and BHARITKAR and MENDEL’s[10]multivalued hysteretic functions.Despite the improvement of the performance of the Hopfield networks over the past decade,this model still has some basic problems and no satisfactory refinement was found,when applied to the TSP[11-12].

In this paper,we introduce a new Hopfield neural network algorithm for efficient solving TSP.Different to the original Hopfield neural network,our architecture uses continuous hysteresis neurons.We prove theoretically that the emergent collective properties of the original Hopfield neural network also are present in the Hopfield network with continuous hysteresis neurons.Simulations of randomly generated neural networks are performed on both networks and show that the Hopfield neural networks with continuous hysteresis neurons have the collective computational properties like the original Hopfield neural networks.What a more,the Hopfield neural networks with continuous hysteresis neuron converges faster than the original Hopfield neural networks do.In order to see how well the Hopfield neural networks with continuous hysteresis neurons do for solving practical combinatorial optimization problems,a large number of computer simulations are carried out for the TSP.The simulation results show that the Hopfield neural network architecture with continuous hysteresis neurons is much better than the previous works including the original Hopfield neural network architecture and Hopfield neural network with hysteresis binary neurons for the TSP in terms of both the computation time and the solution quality.

2 Hopfield Network with Continuous Hysteresis Neurons

For the original Hopfield neural networks,let the output variable yifor neuron i have the rangeand be an continuous and monotone-increasing function of the instantaneous input xito neuron i.The typical input-output relation gi(xi)yi=1/(1+e)shown in Fig.1(a)is sigmoid with asymptotes y0iand y1i.as,

Where r is the gain factor and θ is the threshold parameter.

In biological system,xiwill lag behind the instantaneous outputs yiof the other cells because of the input capacitance C of the cell membranes,the transmenmbrane resistance R,and the finite impedancebetween the output yiand the cell body of cell i.Thus there is a resistance-capacitance(RC)charging equation that determines the rate of change of xi.

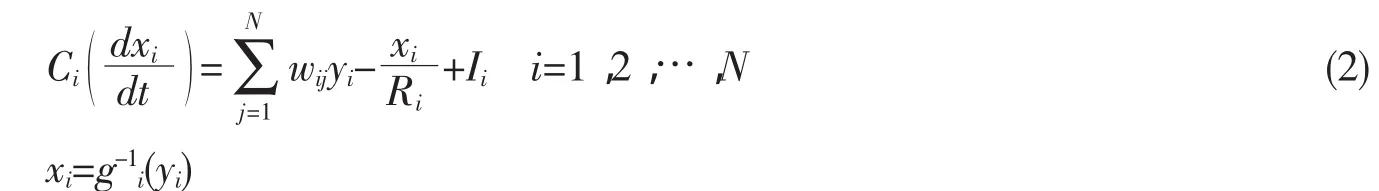
where Ciis the total input capacitance of the amplifier i and its associated input lead.wijyirepresents the electrical current input to cell i due to the present potential of cell j,and wijis thus the synapse efficacy.Iiis any other(fixed)input current to neuron i.In terms of electrical circuits,gi(xi)represents the input-output characteristic of a nonlinear amplifier with negligible response time.It is convenient also to define the inverse output-input relation,

In order to improve the solution quality of TSP,we proposed a new neural network method for efficiently solving the TSP.In this method,a continuous hysteresis neuron is applied to the Hopfield neural network.

The hysteresis continuous neurons change the value of their output or leave them fixed according to a hysteretic threshold rule(Fig.1(b)).Mathematically,hysteretic neuron function is described as:

β＞α,and(γα,γβ)＞0,there is a resistance-capacitance(RC)charging equation that determines the rate of change of xi.

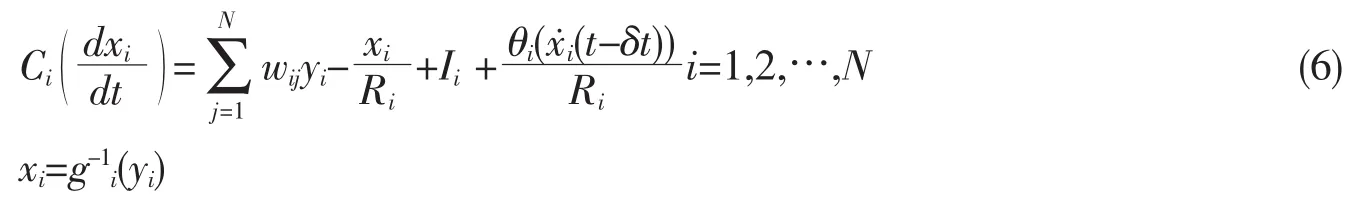
Consider the energy:

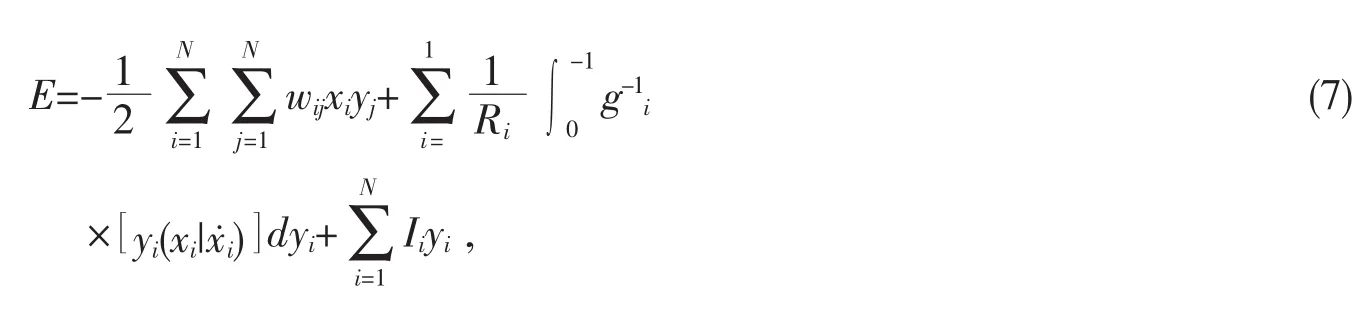
Its time derivative for a symmetric W is:

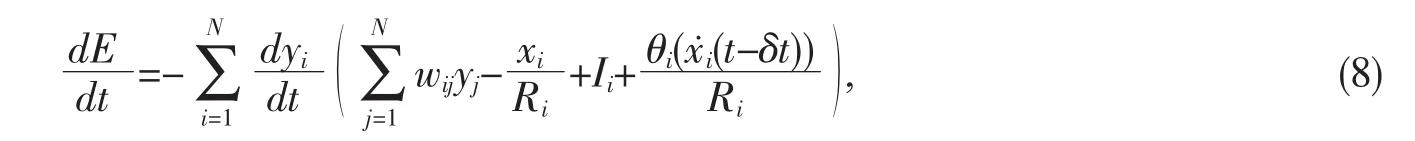
The parenthesis is the right-hand side of Eq.6,so

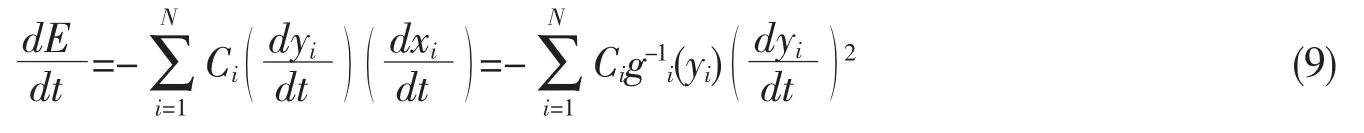
Since g-1i(yi)is a monotone increasing function and Ciis positive,each term in this sum is nonnegative.Therefore:

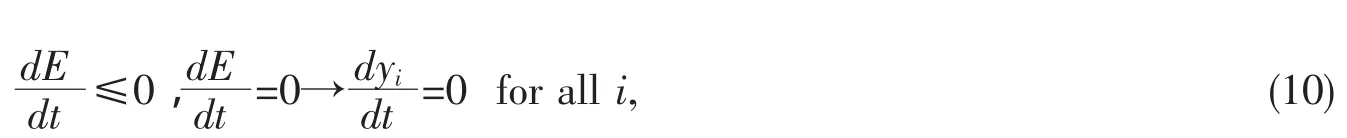
Together with the boundedness of E,Eq.(6)shows that the time evolution of the system is a motion in state space that seeks out minima in E and comes to a stop at such points.E is a Liapunov function for the system.

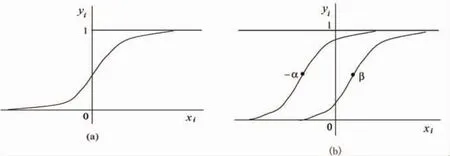
Fig.1 Hysteresis functions图1 连续滞后神经元结构图

3 Application to TSP

The TSP is a classic of difficult optimization problem.It may be stated as follows:given a group of cities to be visited and the distance between each city,find the shortest tour that visits each city only once and re－turns to the starting point.If an initial arbitrary ordering of the N cities is given,a solution to the TSP may be represented as an N×N permutation matrix.Each row of this matrix corresponds to a particular city,while each column corresponds to a particular position in the tour.HOPFIELD and TANK[3]proposed an approach of using a neural network to find a suboptimal solution of the TSP.In their approach,a TSP instance is represented by an energy function including the cost and constraint terms that reflect the objective of a solution.The objective of the constraint term is to find a valid tour,which requires that each city must be visited once and only once.The objective of the cost term is to find the shortest valid tour.

The constraints and the cost function for the TSP can be represented by an energy function.The Hopfield’s original energy function for an N-city TSP is given by[3]:

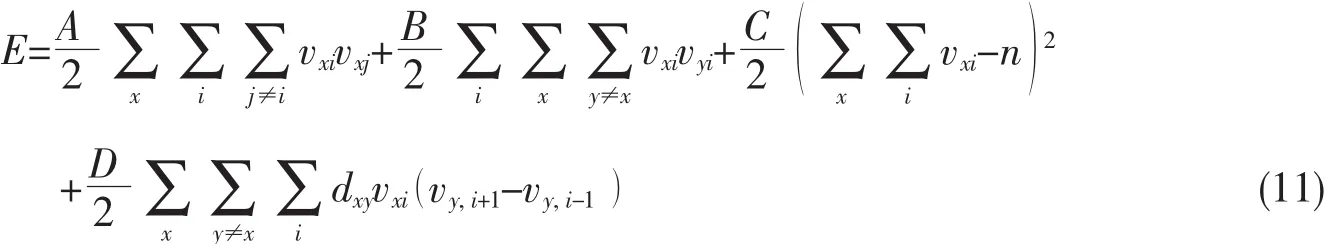
where x and y are row indices;i and j are column indices;vxiis output value for each neuron;dxyis a measure of the distance between cities x and y.The first term will be zero if each row corresponding to a city contains no more than one “1”,with all the other values being zero.Similarly,the second term is zero if each column,corresponding to a position in tour,contains no more than one “1”.The third term is zero if and only if there are N entries of“1”in the entire matrix.The last term represents the distance cost function.

Parameters A,B,C and D,which are all positive constant,are the measure of the importance of the corresponding term.

4 Simulation Results

Experiments were first performed to show the convergence of the Hopfield neural networks with continuous hysteresis neurons.In the simulations,a 100-neuron Hopfield neural network with continuous hysteresis neurons(i=1,2,…,100)was chosen.Initial parameters of the network,connection weights and thresholds were randomly generated uniformly between-1.0 and 1.0.Simulations on a randomly generated 100-neuron Hopfield network with different value of α and β (α=β=0 and α=0.6,β=0.6 for i=1,…,100)were also carried out.Fig.2 shows the convergence charactoristics of both networks.From this figure we can see that both the Hopfield neural networks with continuous hysteresis neurons(α=0.6,β=0.6)converged to stable states that did not further change with time.It is worth to note that the Hopfield neural network with continuous hysteresis neurons (α=0.6,β=0.6)seek out a smaller minimum at seek out E=-158.87 than the Hopfield neural network without hysteresis neurons at E=-127.85(α=β=0).

The Hopfield neural network with continuous hysteresis neurons were also applied to TSP and simulations were also carried out.The proposed algorithm was implemented in C++on PC Station (PentiumIIII 3GHz).A sigmoid function was used as intput/output function and the temperature parameter γα=γβwas set to 0.05.The evaluation in our experiment is based on 100 randomly generated the 10-city TSP data sets,including wide varieties of city distributions.That can reduce the effect of the location distribution of the cities.

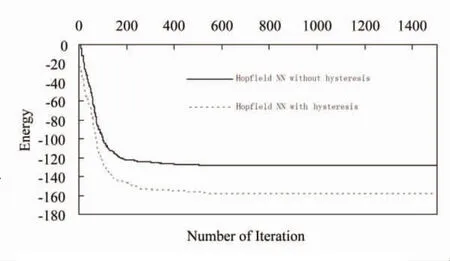
Fig.2 The convergence characteristic of a 100-neuron Hopfield network with and without the continuous hysteresis neurons图2 100个普通神经元与100

The simulations were done using parameters sets at or near A=B=5,C=1,D=2 and n was set to be:n=N+3,where N is the number of city[3].In the simulation,100 runs are conducted for each of the 100 data sets.For each of 100 runs,different random initial states are used.

Fig.3 shows the average number of iterations for converging to valid tour of the 10-city TSP by the Hopfield networks with continuous hysteresis neurons.Each data point shown in Fig.3 is averaged over different runs for each data set and then averaged over 100 different data sets as shown in the following.

The iteration steps of each valid tour j for data set i is averaged over all valid tours:

where Stepiis the average iteration steps for data set i,Nistepis the number of the iteration steps of valid tour j,Nivalidis the number of valid tours among the total 100 runs for data set i.

The iteration steps shown in Fig.3 is the average step in all data set:

We can see in Fig.3 that the Hopfield networks with continuous hysteresis neurons converges to valid tour faster than the original Hopfield network does.The result shows that the networks with continuous hysteresis neurons can obtain valid tours in much fewer numbers of iterations than the network with zero.

Using the similar condition(over 10 data sets),the network with continuous hysteresis neurons was also executed to the 20,30 and 50-city TSP for comparison.Fig.4 shows the average percentage of valid tours of the 20,30,50-city TSP by the Hopfield networks with different continuous hysteresis neurons.Fig.5 shows the average number of iterations for converging to valid tour of the 20,30,50-city TSP by the Hopfield networks with continuous hysteresis neurons.The simulation results show that the Hopfield networks with positive parameter has a rate of success higher than original Hopfield network for solving the TSP,and converges faster to valid solution than the original Hopfield network does.

Fig.3 The average number of iterations for converging to valid tour of the 10-city TSP by the Hopfield networks with different α and β(α+β=-2.0,-1.8…6.0)图3 α与β取不同值时(α+β=-2.0,-1.8…6.0),10城市TSP问题的收敛性

5 Conclusions

We have proposed a continuous hysteresis Hopfield neural network architecture for the TSP,and showed its effectiveness by simulation experiments.The proposed architecture was based on a modified Hopfield neural network in which the continuous hysteresis neurons were added to improve solution quality.We proved theoretically that the emergent collective properties of the original Hopfield neural network also were present in the Hopfield neural network architectures with continuous hysteresis neurons.A large number of computer simulations have been carried out for the TSP to verify the potential of this network in combinatorial optimization problems.The simulation results showed that the Hopfield neural network architecture with continuous hysteresis neurons was much better than the previous works including the original Hopfield neural network architecture for TSP in terms of both the computation time and the solution quality.

Fig.4 The average percentage of valid tours of the 20,30,50-city TSP by the Hopfield networks with different α and β(α=β=-0.5,0,1.5)图4 α与β取不同值时，20、30、50城市TSP问题的有效平均百分比

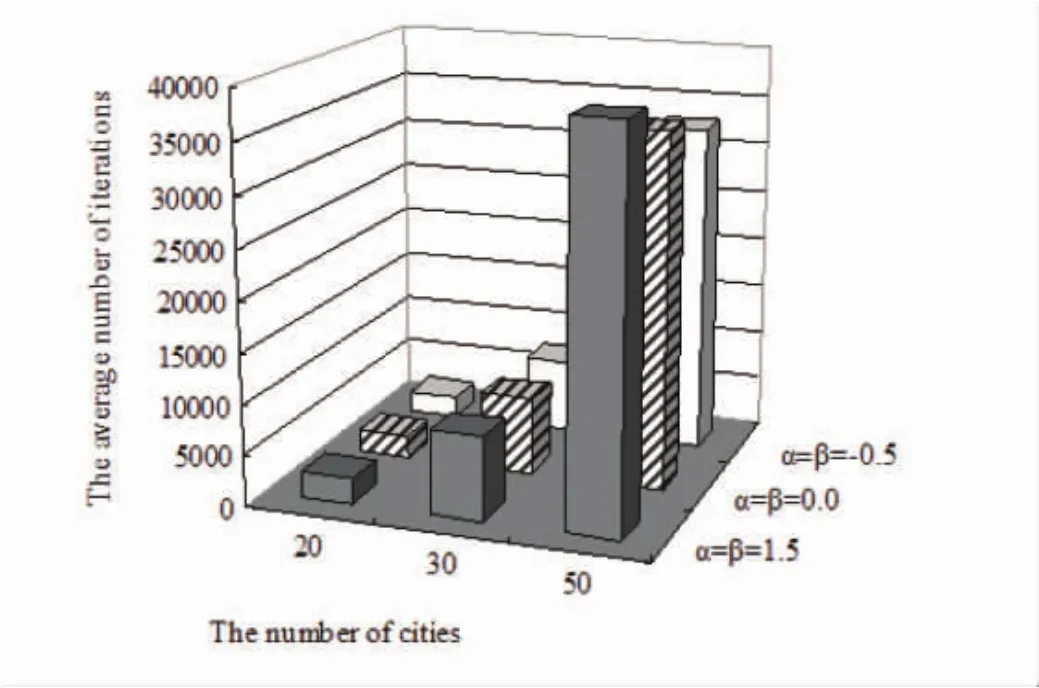
Fig.5 The average number of iterations for converging to valid tour of the 20,30,50-city TSP by the Hopfield networks with different α and β(α=β=-0.5,0,1.5)图5 α与β取不同值时，20、30、50城市TSP问题的有效平均迭代次数

[1]HOPFIELD J J.Neural network and physical systems with emergent collective computational abilities[J].Proc Natl Acad Sci(USA),1982,79:2 554-2 558.

[2]HOPFIELD J J.Neurons with graded response have collective computational properties like those of two-state neurons[J].Proc Natl Acad Sci(USA),1984,81:3 088-3 092.

[3]HOPFIELD J J,TANK D W.‘Neural’computation of decisions in optimization problems[J].Biol Cybern,1985,52:141-152.

[4]HOPFIELD J J,TANK D W.Computing with neural circuits:a model[J].Science,1986(233):625-633.

[5]TANK D W,HOPFIELD J J.Simple neural optimization network:An A/D converter,signal decision circuit,and linear programming circuit[J].IEEE Trans,Circuits&Systems,1986,CAS-33(5):533-541.

[6]TAKEFUJI Y,LEE K C.An hysterisis binary neuron:A model suppressing the oscillatory behavior of neural dynamics[J].Biol Cybern,1991,64:353-356.

[7]TATEISHI M,TAMURA S.Comments on Artificial neural networks for four-coloring map problems and K-colorability problems'[J].IEEE Trans Circ Syst-I:Fundamental Theory and Applications,1994,41(3):248-249.

[8]WANG L.Discrete-time convergence theory and updating rules for neural networks with energy functions[J].IEEE Trans Neural Networks,1997,8(5):445-447.

[9]Galán-Marín G,Muñoz-Pérez J.A new input-output function for binary Hopfield neural networks[C]//Proceedings of the International Work-Conference on Artificial and Natural Neural Networks:Foundations and Tools for Neural Modeling,1999:311-320.

[10]BHARITKAR S,MENDEL J M.The hysteretic Hopfield neural network[J]IEEE Trans Neural Networks,2000,11(4):879-888.

[11]COOPER B S.Higher Order Neural networks-can They Help us Optimize?[C]//Proceedings of the Sixth Australian Conference on Neural Networks(ACNN’95).1995:29-32.

[12]VAN DEN BOUT D E,MILLER T K.Improving the Performance of the Hopfield-Tank Neural Network through Normalization and annealing[J].Bio Cybern,1989,62:129-139.