基于现场可编程门阵列的广义逆矩阵求解
赵 兵,赵辽英
(杭州电子科技大学计算机应用研究所,浙江杭州310018)
0 引言
近几年,现场可编程门阵列正被越来越多的用于各种矩阵运算[1],如定点、浮点数的运算,矩阵乘法[2],矩阵求逆[3,4],矩阵特征值分解[5]等。一般的逆矩阵只是对非奇异矩阵才有意义。实际问题中遇到的矩阵不一定是方阵,即使是方阵也不一定是非奇异的,广义逆是奇异方阵和一般矩阵的广义逆[6]。目前基于可编程门阵列的矩阵求逆设计与实现都只适合非奇异矩阵的求逆,针对广义逆的硬件实现研究未曾报道。本文提出了基于迹方法求矩阵广义逆的可编程门阵列实现方案,对这一领域的研究具有一定的参考价值。
1 矩阵的广义逆求解算法
矩阵的广义逆求解方法主要有方程求解法、KL分解法、递推法和迹方法[6]4种,其中迹方法精炼明确,也便于并行计算设计,所以本文选用了此方法来求解矩阵的广义逆。
1.1 矩阵广义逆求解的迹方法
设已知矩阵Am×n的秩为r,矩阵求广义逆的算法如下:
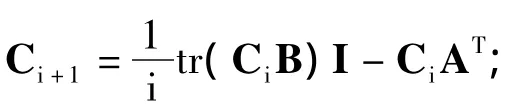
1.2 基于初等行变换的矩阵求秩
求矩阵伪逆的迹方法需要已知矩阵的秩,矩阵的初等行变换可以确定矩阵的秩[7]。
先给出Hermite标准型的定义[7]。
定义1 设B∈Cm×nr(r>0),且满足:
(1)B的前行中每一行至少含一个非零元素,且第一个非零元素是1,而后m-r行元素为零;
(2)若B中第i行的第一个非零元素1在第ji列(i=1,2,…,r),则j1<j2<…jr;
(3)B中的j1,j2,…,jr列为单位矩阵Im的前r列。那么就称B为Hermite标准形。
显然,任意非零矩阵A∈Cm×nr可通过初等行变换化为Hermite标准形B,且B的前r行线性无关,其中r就是矩阵的秩。
矩阵的初等行变换有3种:(1)对调两行;(2)以数k(k≠0)乘某一行的所有元素;(3)把某一行所有元素的k倍加到另一行对应的元素上去。3种初等行变换结合使用,可以将任意非零矩阵化为Hermite标准型,3种变换中的第1、2两种变换很容易实现,但第3种变换比较繁琐,目的是将矩阵中某元素所在列的其余元素全化为0。针对第3种变换,文献8给出了一种矩形对角线计算法。通过分析,可以发现该算法具有很强的并行性,非常适合用可编程门阵列实现。
2 算法的可编程门阵列实现
根据算法描述,将硬件实现电路划分为5个主要模块:控制模块、数据暂存模块、矩阵乘法模块、矩阵求秩模块、广义逆求解模块。硬件系统结构框图如图1所示。

图1 系统硬件结构框图
2.1 控制模块和矩阵乘法模块
控制模块负责协调系统各个功能子模块的运行,控制着数据流的流向和各个模块的动作运行的开始和停止。矩阵乘法计算模块是由一系列乘累加运算组成的,是计算量比较大的模块,耗时也比较多。因此把矩阵乘法模块单独拿出来进行设计,与矩阵求秩模块并行来进行计算,提高了设计的并行性,从而提高系统的运算速度。本文调用了4个单精度浮点乘法IP核和4个单精度浮点加法IP核组成浮点乘累加运算单元,进而组成4×4浮点矩阵乘法运算模块。
2.2 矩阵求秩模块
算法中要求已知矩阵的秩r(A)。求秩模块不仅在最后求解广义逆模块用到,而且控制着循环计算模块的循环计算次数。根据矩形对角线计算法[8]设计如图2所示的硬件结构。根据算法流程对矩阵求秩模块进行详细的模块划分。顶层模块主要包括控制模块、数据输入、数据存储、接口模块、选主元模块、主元化为1(行倍乘运算)、行交换和数据输出8个子功能模块。控制模块(control module),用来启动和停止数据的流动,接收状态条件以并根据状态条件决定下一步需要做什么。需要将控制模块设计成状态机。整个模块的运行是在状态机控制下有序进行的,把整个运算过程分解为几个按一定顺序进行的子过程来进行运算实现,而子过程刚好可以用对应状态来表示,子过程进行顺序计算的过程刚好对应状态转换的过程。因此可以用状态机的思想来实现整个运算过程。
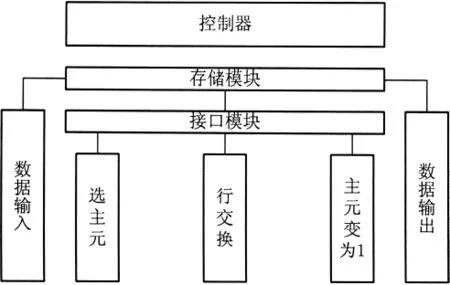
图2 矩阵求秩模块结构
2.3 伪逆计算模块
广义逆求解模块的核心模块是循环计算模块。正如前文所述矩阵的秩是一个关键参数就体现在这一模块中,更新矩阵的循环计算过程中矩阵的秩r直接控制着循环计算的次数。广义逆计算模块在求出矩阵秩r后开始工作的。核心模块循环计算模块包括矩阵求迹,矩阵减法,矩阵乘法运算。求矩阵迹可以通过对对角线元素进行累加即可实现,矩阵乘法可以调用前边所用的矩阵乘法模块,矩阵减法实现比较简单,只需要读取存储在存储器中的矩阵数据输入减法器按顺序计算。
3 实验仿真结果分析
软件程序的编写和仿真采用Mathworks公司的MATLAB R2010a软件环境,输入非奇异方阵

硬件仿真波形输出如图3所示。系统设计用Verilog HDL语言来描述,电路的综合采用Altera公司的Quartus II 9.1软件完成。结果数据采用单精度浮点十六进制数表示。

图3 硬件仿真结果波形图
从仿真波形可以看出,硬件仿真结果与软件仿真结果完全吻合。求取10次运算的平均用时得出用MATLAB求解示例矩阵广义逆耗时约7.5ms;用同样的矩阵进行广义逆求解运算实验,通过仿真验证可以得出采用现场可编程门阵列的方案仅用时约15μs,说明对于4×4的奇异方阵求逆,硬件实现在保证结果精确的基础上运算速度提高了近500倍。
4 结束语
本文通过对矩阵求广义逆算法的理论分析,阐述了矩阵求广义逆的硬件实现方法,再用Matlab和Quartus II分别进行了软硬件代码仿真。结果表明硬件实现在保证结果精确的基础上大大提高了运算速度。由于充分利用了硬件的速度优势,矩阵求广义逆的可编程门阵列实现非常适合于要求算法实时性高的领域。并且,经过适当配置,本设计可以用来求解其它任意矩阵的广义逆。因而比采用专用ASIC(专用集成电路)的方法具有更高的灵活性,同时也节约了成本。
[1] 周宁宁,陈燕例,李爱群.基于FPGA技术的浮点运算器的设计与实现[J].计算机工程与设计,2005,26(6):1 578-1 581.
[2] Ioannis Sotiropolos,Ioannis Papaefstathiou.A Fast Parallel Matrix Multiplication Reconfigurable Unit Utilized in Face Recognitions Systems[C].Prague:IEEE International Conference on Field Programmable Logic and Applications,2009:276-281.
[3] 王锐,胡永华,马亮,等.任意维矩阵求逆的FPGA设计与实现[J].中国集成电路,2007,16(4):51-56.
[4] 李涛,张忠培.矩阵求逆的FPGA实现[J].通信技术,2010,43(11):147-149.
[5] 王飞,王建业,张安堂,等.实对称矩阵特征值分解高速并行算法的FPGA实现[J].空军工程大学学报(自然科学版),2008,9(6):67 -74.
[6] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004∶85-93.
[7] 房月华,陈萍.矩阵的满秩分解及其方法[J].衡水学院学报,2011,13(4):16-18.
[8] 夏日,张裕生.对矩阵初等行变换的算法改进[J].工科数学,1994,10(3):121-123.

