基于概率极限状态的RAIM风险评估

杨传森，徐肖豪

（1．金陵科技学院机电工程学院，南京211169；2.中国民航大学空中交通管理研究基地，天津300300）

基于概率极限状态的RAIM风险评估

杨传森1，徐肖豪2

（1．金陵科技学院机电工程学院，南京211169；2.中国民航大学空中交通管理研究基地，天津300300）

为了提供准确可靠的完好性服务，提出了基于概率极限状态的RAIM完好性风险评估。考虑所需导航性能参数和噪声的因素，建立了安全系数与可靠系数相结合的完好性风险评估指标体系，确立风险评价准则。非精密进近的算例分析表明，系统评估方法是可行的且有效的。

接收机自主完好性监测；概率极限状态；所需导航性能；非精密进近；漏检率

为了提供更精确可靠的完好性服务[1]，保障飞行安全，需要研究用户端接收机自主完好性监测（receiver autonomous integrity monitoring，RAIM）算法。RAIM利用用户接收机的冗余观测值监测用户定位结果的可靠性，保障定位的精度[2]。文献[3]利用机载气压高度表来增强RAIM，提高了故障检测灵敏性，但只适合于单故障目标。文献[4]提出了基于最小二乘残差RAIM改进算法，考虑了卫星几何分布和漏检率因素，但没有考虑噪声较大的情况。针对Snapshot RAIM对多故障不敏感的缺陷，文献[5]提出了将时域处理和集合统计综合实现RAIM算法，但是，有偏估计会造成斜坡故障变大，导致检测失效或错误，甚至导致卡尔曼滤波器发散。文献[6]提出了假设验证法RAIM算法用于卫星导航多星故障识别，但是，对于多系统兼容接收机，由于可视卫星数量多，导致假设验证的情况增多，计算量大幅增加，会破坏接收机的自主完好性。

实际上，全球导航卫星系统（GNSS）定位精度容易受到时间同步、轨道确定、传播时延和几何精度因子影响；传播时延有不确定性，各航段的完好性要求存在差异，且完好性与其他参数之间具有相关性。而现有RAIM研究算法一般是通过预设阈值并进行一致性检测来实现完好性监测[7-8]，提供快速报警，即为RAIM定值分析法[9]。基于定值分析法的RAIM算法是建立在确定性基础上，用此方法来描述具有复杂性、不确定性和自有相关性的系统是不适宜的。

随着GNSS发展，基于多卫星系统组合导航的传统RAIM改进与优化算法，应用于含有垂直引导的LPV200航段[10-12]并取得一定效果。从本质上说，组合导航是一种多传感器的数据融合而获得的对环境或目标状态的最优估计的导航方法[13]，进一步提高了整个系统的复杂性。不同于传统的“非有即无”式的确定性的定值分析法，概率极限状态分析法是以概率理论为基础，计算系统的故障概率来确定系统安全与可靠的方法[14]，也是对系统同时具有确定性和随机性的两重性的认识结果。因而，它能有效地解决系统内实际存在的复杂性和不确定性。

针对不同航段上完好性差异、噪声不确定性，文献[14]提出了概率极限状态，由于存在边界状态，发生概率虽小，但发生后易造成灾难性后果的风险，缺乏对其风险性评估进行探讨。本文针对导航系统的复杂性（例如，不同航段上存在完好性差异、噪声不确定性）等特点，将定值分析和概率分析相结合，进一步探讨并建立有效实用的安全系数与可靠系数相结合的RAIM完好性风险评价体系，并提出评价准则。最后的算例分析将验证该评价体系的可行性和有效性。

1 基于概率极限状态RAIM算法

文献[14]首先采用概率极限状态模型对RAIM算法进行分析，并设计与漏检率Pf有着一一映射关系的可靠指标β进行概率度量，给出可靠指标β求解方法以及故障检测和故障识别方法。

1.1 概率极限状态函数

考虑到噪声对定位误差的影响，定义概率极限状态函数

其中：RNPΔX是所需导航性能规定所允许的限定值；ΔX和V分别是由伪距偏差和噪声产生的定位误差，两者之差表示真实定位误差，且两者相互独立，各自服从正态分布N（μΔx^，σΔx^），N（μv^，σv^），因此R也服从正态分布N（μR，σR）。

若定义fV（v）·dv为观测噪声在区间（v，v+dv）上的概率，FΔX（v）为P（R≤0），且在V的全域内积分，有Pf为漏检率

1.2 可靠指标β求解

用指标β来代替Pf概率度量，使得β和Pf有着一一映射关系，如表1所示。在各个航段上，漏检率均取0.001，即对应的β取值3.1。

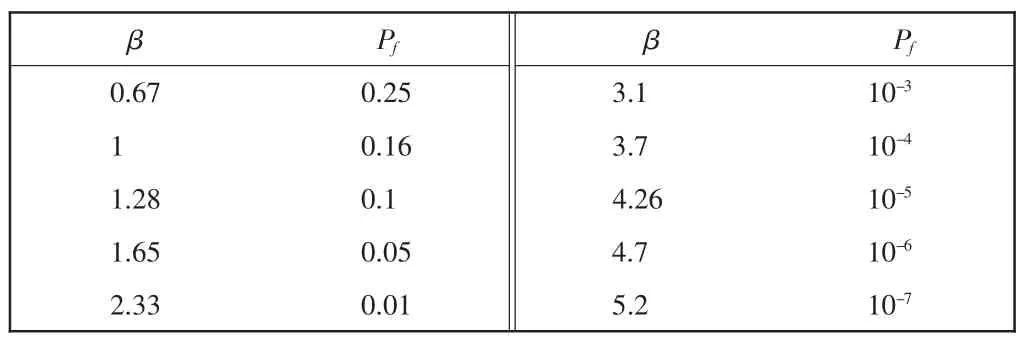
表1 指标β与Pf漏检率的一一对应关系表Tab.1 Single-valued mapping between index β and probability Pf

在式（1）中，将变量ΔX和V作正则化处理，有

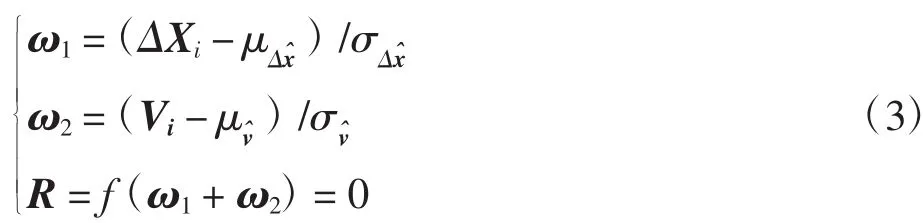
方程f（ω1+ω2）=0是以β为半径的球面方程的公切面。有约束条件

拉格朗日乘数因子法是解极值问题的有效方法，其中

将式（5）代入式（3）中，通过迭代计算，可获得可靠指标β数值解[14]。

1.3 故障检测

故障检测是RAIM算法的首要任务。它主要判断是否存在故障卫星，及时发现导航中的异常情况，避免飞行危险。根据在各个航段上，漏检率均取0.001，即对应的β取值3.1。选定预定漏检率对应的β值作阈值βT，如果实际β估算值大于阈值βT，则认定系统无故障，否则，认定系统有故障。即有

1.4 故障识别

在故障识别过程中，需将卫星定位误差真值与航段定位误差保护限值相比较。如果大于航段定位误差保护限值就认定为故障星

其中敏感误差矩阵D为

测量值z是一个列向量，包括两个部分：有偏值和无偏值，设z1为无偏值，z2为有偏值，并假设第j个参数含有错误，其值记为bj，有

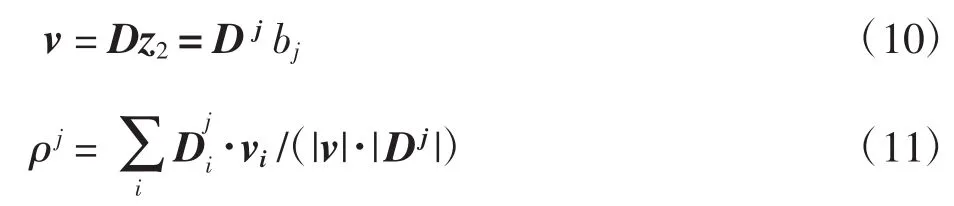
其中：Dj为D矩阵第j行对角元素。如果相关系数ρj的绝对值等于1，在理论上可以说明第j颗卫星有错误。用ej表示第j颗星的误差真值，有

2 完好性风险评估体系

概率极限状态存在边界状态，极值风险发生概率虽小，一但发生超出边界状态的事件，容易造成灾难性后果。针对导航系统的复杂性等特点，建立有效实用的安全系数与可靠系数相结合的完好性风险评估体系并提出评价准则，进行风险性评估。研究内容包括：安全系数、变异系数与可靠系数以及完好性风险评估体系的评价准则。

2.1 安全系数

安全系数定义为

其中：U表示导航性能规定所允许的定位误差；V表示定位误差的综合效应。变量（x1x2…xn）是定位误差的影响因素。实际取值中均有一定的变异性，可视为随机变量，服从正态分布。变量（x1x2…xn）的平均值为，即F的数学期望E（F），也是通常意义下的安全系数。

由于存在边界状态，安全系数法是建立在确定性之上的定值分析法。传播时延存在不确定性，航段的完好性存在差异，完好性参数之间具有相关性。为克服上述因素及噪声带来的缺点，建立在不确定概念之上的概率分析方法被引入性能评价之中，基本思想是以安全系数为基础，利用可靠指标计算模型求出可靠系数。

2.2 变异系数

假设安全系数F的方差D（F）可知，则安全系数的变异系数定义为

同样的安全系数，可靠性却不一样。由于计算参数是离散的，具有变异性、相关性，导致“反常”现象：有时会出现安全系数大于l却发生破坏，造成重大损失；安全系数小于1，却是安全的。实际的安全系数不一定恰恰好是分子和分母的均值之比，因此产生这种反常现象是很正常的。

在非精密进近阶段参数U是定值556 m，假设故障漏检概率为0.001，用户定位误差均方差σ=30 m，表2是F函数的参数V的变异性对系统稳定性的影响，其安全系数均相同，均为1.85大于1，但仍存在不稳定的可能，其故障概率也是不一样的，变异系数越大，破坏概率越大。因此，系统可靠性随参数V的变异性增加而减少，其不确定性对系统稳定性的影响是非常灵敏的。

表2 参数V变异性对系统可靠性的影晌Tab.2 Influence of parameter V variability on system reliability

2.3 可靠系数

可靠系数定义为可靠指标比率βr与系统无故障概率（1-PF）乘积，共同度量系统的稳定性，记为Re

2.4 完好性指标体系的评价准则

依据安全系数F0和变异系数δF，计算故障概率PF（以此故障概率为漏检率限值），且以变异系数为变量，得到安全系数在不同变异系数下的故障概率。根据式（17）将可靠指标比率与系统可靠概率相乘，对可靠指标与其阈值之比进行折减，得到系统安全的可靠系数。最大可能可靠系数R0与临界故障概率P0计算值列于表3。图1反映了可靠指标与临界故障概率的响应曲线。

表3 最大可能可靠系数与临界故障概率Tab.3 Maximum possible reliability coefficient and critical failure probability

完好性指标体系的评价准则：

1）可靠系数大于1，系统稳定可靠；

2）可靠系数小于1，系统失稳且不可靠；

图1 可靠指标与临界故障概率响应曲线Fig.1 Curves of reliability index and critical failure probability

3）可靠系数等于1，系统处于极限状态，不可靠。

根据可靠系数的状态，可计算出不同最大可能可靠系数和临界故障概率。由此获得可靠指标和故障概率联合判别系统稳定性与可靠性。

3 算例与分析

以GNSS导航系统为例，通过非精密进近算例进行完好性指标分析，验证可靠指标和失效概率联合判别系统稳定性与可靠性。

3.1 参数设置

在算例中，完好性指标体系依然采用式（17）所建立的可靠系数来体现。各项参数设置列于表4，其中RNPΔX取为非精密进近的所需导航性能规定的参数，定位偏移参数ΔX和噪声V为随机变量，且ΔX和V相互独立且均服从正态分布。

表4 参数ΔX与VTab.4 Parameter ΔX and parameter V

3.2 实验方法与模拟成果

采用蒙特卡罗方法，得到故障概率与安全系数构成的模拟计算如表5所示。

由表5知模拟次数为20万次时，误差为2.7×10-5。事实上，从N=10万次起，相邻两次的破坏概率差值小于0.000 04，说明故障概率趋于稳定，已经收敛。因此，可将N=20万次对应的故障概率作为系统的漏检率，即Pf=2.8×10-4，可靠指标β=3.450 3。安全系数的平均值为1.317 8，与F0安全系数相近（首先取ΔX、V均值，将参数代入式（13），计算系统处于极限平衡状态对应的系统的安全系数F0=1.308 2）。计算得到的系统可靠系数大于1，并趋近于1.115，如图2所示。

表5 蒙特卡罗模拟结果Tab.5 Result of Monte-Carlo simulation

图2 可靠系数响应图Fig.2 Response of reliability coefficient

可靠指标β=3.450 3，系统处于无告警状态，但仍需要对系统稳定性与可靠程度进行评估。

3.3 系统可靠性验证

图3为采用蒙特卡罗法模拟非精密进近过程的系统稳定性与可靠性的结果。

图3 系统状态分布Fig.3 System state distributions

在系统稳定性与可靠性验证中，采用矩估计法来计算安全系数的均值与方差。安全系数的均值和方差分别为

所得安全系数略高于1.317 8与1.308 2。由式（14）计算变异系数，由式（15）计算的故障概率Pf=0.003 7（μF=1.318 85，σ2F=0.014 147）。阈值 βthreshold取为3.1，根据式（17）计算的可靠系数为3.564，以上结果并分析，对照图3，系统处于稳定状态。

4 结语

本文以GNSS导航系统为例，综合考虑航段上RNP定位误差保护限值和噪声的影响，建立了定值分析和概率分析相结合的完好性风险评估指标体系，并详细阐述了形成过程，提出了风险评价准则；给出了非精密进近算例，模拟了完好性风险评估过程，验证了风险评价的安全与可靠性。在拓展了现有的极限概率算法的基础上，为解决完好性风险评估提供了一种新方法。

[1]WANG JINLING，OBER P B.On the availability of fault detection and exclusion in GNSS receiver autonomous integrity monitoring[J].The Journal of Navigation，2009，62：251-261.

[2]孙明菡，孙国良.接收机自主完好性检测可用性判断方法研究[J].遥测遥控，2006，27（2）：24-27.

[3]刘 准，陈 哲.GPS自主式完整性检测技术研究[J].北京航空航天大学学报，2003，29（8）：673-676.

[4]陈小平，滕云龙.接收机自主完好性监测算法研究[J].电子科技大学学报，2008，37（2）：218-220.

[5]孙国良，孙晓萌，陈金平.时-集综合的接收机自主完好性监测方法研究[J].航空学报，2006，27（6）：1171-1175.

[6]张 强，张晓林，常啸鸣.用于卫星导航多星故障识别的新方法[J].航空学报，2008（5）：1239-1244.

[7]OCHIENG W Y.GPS integrity and potential impact on aviation safety[J].The Journal of Navigation，2003，56：51-65.

[8]ENEA，BLANCHJ，WALTERT.Galileo-GPS RAIM for Vertical Guidance[C]//Proceedings of ION NTM 2006，Monterey，CA，18-20 January，2006.

[9]徐肖豪，杨传森，刘瑞华.GNSS用户端自主完好性监测研究综述[J].航空学报，2013，34（3）：451-463.

[10]CHOI M，BLANCH J，WALTER T，et al.Demonstrations of Multi-Constellation Advanced RAIM for Vertical Guidance Using GPS and GLONASS Signals[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation（ION GNSS 2011），Portland，OR，Sep 2011：3227-3234.

[11]BLANCH J，WALTER T，ENGE P，et al.Critical elements for a multi-constellation advanced RAIM[J].Navigation，2013，60（1）：53-69.

[12]LEE Y C.New advanced RAIM with improved availability for detecting constellation-wide faults，using two independent constellations[J].Navigation，2013，60（1）：71-83.

[13]姚 静，易东云，朱炬波.多种导航卫星系统的组合共用技术探讨[J].全球定位系统，2008（2）：31-36.

[14]YANG CHUANSEN，XU XIAOHAO，LIU RUIHUA，et al.New algorithm for receiver autonomous integrity monitoring[J].Transactions of Nanjing University of Aeronautics and Astronautics，2010（2）：155-161.

（责任编辑：杨媛媛）

Risk assessment for receiver autonomous integrity monitoring based on probability limit state

YANG Chuan-sen1，XU Xiao-hao2
（1．College of Mechanical and Electrical Engineering，Jinling Institute of Technology，Nanjing 211169，China；2．Research Base of Air Traffic Management，CAUC，Tianjin 300300，China）

In order to provide accurate and reliable integrity service，the integrity risk assessment for receiver autonomous integrity monitoring based on probability limit state is proposed.Taking into account the required navigation performance parameters and noise factors，the system indices of the integrity risk assessment are established combining with the safety factor and reliability coefficient.And then，the evaluation criterion is established for the integrity risk assessment of receiver autonomous integrity monitoring reliability.Simulation for non-precision approach validates both feasibility and effectiveness of the proposed algorithm.

receiver autonomous integrity monitoring；probability limit state;required navigation performance；nonprecision approach；missed detection probability

V249；P228.4

A

1674－5590（2013）06－0016－05

2013-05-13；

2013-08-26

金陵科技学院博士启动基金项目（JIT-b-201226）

杨传森（1968－）,男,安徽合肥人,讲师，博士，研究方向为卫星导航自主完好性监测.