基于无限长均匀带电圆柱壳产生的静电场的探讨
张丽琴,张金锋,徐士涛,尹新国
(淮北师范大学 物理与电子信息学院,安徽 淮北 235000)
基于无限长均匀带电圆柱壳产生的静电场的探讨
张丽琴,张金锋,徐士涛,尹新国
(淮北师范大学 物理与电子信息学院,安徽 淮北 235000)
静电场是物理学中重要内容之一,本文主要通过静电场高斯定理、电势的定义式计算了无限长均匀带电圆柱壳的电场强度及电势的分布,最后通过讨论得到无限长均匀带电圆柱面、无限长均匀带电圆柱体的电场强度及电势.本文可有助于学生对静电场高斯定理的理解及应用,并加深对电场强度、电势计算方法的掌握.
静电场;无限长;均匀带电;圆柱壳;高斯定理
众所周知,静电场的高斯定理说明静电场是有源场,而安培环路定理又说明它是无旋场,即静电场是有源无旋的保守力场[1-2].一般带电体电场强度主要利用电场强度的叠加原理来计算,文献[3-5]指出对于一些具有高度对称性的带电体通常利用静电场的高斯定理计算比较简单.关于静电场电势的计算有很多种方法,主要利用电势的叠加原理或者电势的定义式l进行计算[6-7].本文主要利用高斯定理计算了无限长均匀带电圆壳的电场强度,并利用电势的定义式计算其电势分布,最后通过讨论得到无限长均匀带电圆柱体及无限长均匀带电圆柱面的电场强度及电势分布.
1 无限长均匀带电圆柱壳产生的电场强度
真空中有一个无限长均匀带电圆柱壳,内部是空腔,圆柱壳内外半径分别为R1和R2,电荷的线密度仍为λ,其截面如图1所示,A、B、C三点代表r

图1 无限长均匀带电圆柱壳的截面图
分析 由于带电体的电荷分布具有高度的轴对称性,可知电场强度也具有轴对称性,可知电场场强的方向与圆柱面的中心轴垂直.过A、B、C三点分别做半径为rA、rB、rC,高为L的同轴心闭合圆柱高斯面,如图1所示,则电场场强的方向也与高斯面的侧面垂直,而与高斯面的上下底面平行.
当R1 同理可知当r 当r≥R2时 令R2=3R1,由此可得,无限长均匀带电圆柱壳的的电场强度大小分布情况如图2所示: 图2 无限长均匀带电圆柱壳所激发电场强度示意图 在计算电势之前必须先规定电势零点,为了计算方便起见,电势零点选在带电圆柱壳的外表面上 当r 利用公式(1)、(2)可得 当R0≤r 当r≥3 R1时,利用公式(3)得 令R2=3R1,则无限长均匀带电圆柱壳产生的电势分布曲线如图3所示: 图3 无限长均匀带电圆柱壳的电势分布曲线 当R0→0时,无限长均匀带电圆柱壳的空腔缩为一线,即圆柱壳就变成半径为R2圆柱体.将R0→0带入公式(1)、(3)、(5)、(6)得,无限长均匀带电圆柱体产生的电场强度和电势. 当r 当R1→R2时,无限长均匀带电圆柱壳就变成半径为R2无限长均匀带电圆柱面.R1→R2带入公式(2)、(3)、(4)、(6)得,无限长均匀带电圆柱面产生的电场强度和电势. 当r 利用洛必达法则求极限[8],可得 带入上式可得 r>R2时 在静电场中有很多非常重要的带电模型,如:均匀带电球体、均匀带电球面、无限长均匀带电圆柱体、无限长均匀带电圆柱面、无限大均匀带电平面等,几乎所有的大学物理教材都会涉及到这些带电模型电场强度、电势的计算.计算具有高度对称性的带电体所产生的电场强度时,通常选择静电场的高斯定理比较简单、方便,但是问题的关键是选择合适的高斯面,然后利用电势的定义式计算其大小. 〔1〕张玉民,戚伯云.电磁学[M].北京:科学出版社,2007.24-50. 〔2〕胡盘新,等.普通物理学简明教程(上)[M].北京:高等教育出版社,2007.56-61. 〔3〕张清泽,等.对高斯定理特性和应用的认识[J].高等函授学报,2011(1):29-30. 〔4〕张平伟.关于高斯定理的一个疑问[J].安庆师范学院学报,2012,18(2):124-126. 〔5〕李自华.高斯定理的理解及应用[J].廊坊师范学院学报,2009,9(3):55-56. 〔6〕张之翔.均匀带电圆环的电场强度[J].大学物理,2012,31(5):14-16. 〔7〕官邦贵,等.电场强度的几种计算方法及讨论[J].科技信息,2010,29(2):17-18. 〔8〕张再云,等.极限计算的方法与技巧[J].湖南理工学院学报,2009,22(2):16-19. O441 A 1673-260 X(2013)10-0010-02 淮北师范大学校级青年基金项目(2012xq36);安徽省高等学校质量工程项目(2011248);物理学(师范)特色专业建设点(800551)




2 无限长均匀带电圆柱壳产生的电势

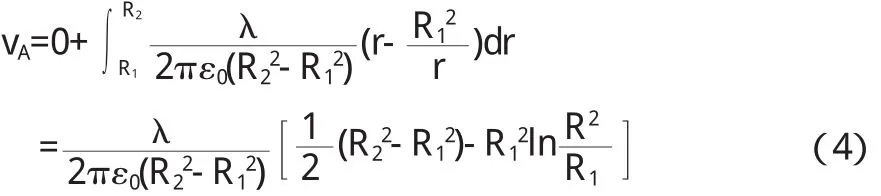



3 讨论与推广






4 结束语

