二元有理插值函数的构造新方法
荆科
(阜阳师范学院数学与计算科学学院,安徽阜阳236041)
二元有理插值函数的构造新方法
荆科
(阜阳师范学院数学与计算科学学院,安徽阜阳236041)
二元有理插值函数的构造方法大都是基于连分式进行的.本文利用二元拉格朗日插值函数的误差理论思想,建立一种二元有理插值公式.相对于其他的插值方法,本文所构造的二元有理插值函数具有次数较低,有更多的灵活性,计算量少,便于实际应用等特点.
二元有理插值函数;拉格朗日基函数;插值公式;二元多项式
1 引言
有理函数属于简单函数类,它比多项式复杂,用它近似表示函数时,却比多项式灵活,更能反映函数的一些特性.矩形网格上的二元多项式插值问题是适定的(解存在且唯一),但是二元有理插值问题没有多项式插值类似的结果.

其中p(x,y),q(x,y)均是二元多项式.
而目前构造有理插值函数的方法主要都基于连分式给出的,文[1]中为了解决有理插值函数的存在性问题,采用了混合方法或分块方法,但是构造的有理函数次数较高,且计算量较大.文[2]中利用牛顿基函数的方法给出了二元有理插值函数的表达式

文[3]中利用拉格朗日基函数的方法给出了二元有理插值函数的表达式

虽然文[4]利用牛顿差商的性质简化了文[2]中的方程组的系数矩阵.但是,无论是文[2-4]都需要求解线性方程组,且如果解的某个分量qij=0时,就会产生不可达点.而且在确定有理插值函数类型之前并不能判断其是否存在qij=0;另外,一旦插值节点和有理插值函数的次数给定,p(x,y)和q(x,y)也是唯一确定的,这样也就使二元有理插值函数丧失了很多灵活性,并且计算p(x,y)和q(x,y)的表达式也需要较大的计算量.
2 有理插值公式
本文利用二元多项式插值理的误差理论思想,建立二元有理函数插值公式,既降低了有理插值函数的次数,且与文[5]中推广文[7]的算法相比具有计算量低等特点.
定理1[6]矩形网格∏m,n={(xi,yj)/(xi,yj)∈R2,i=0,1…,m,j=0, 1,…,n}上的二元拉格朗日插值公式为:

其中
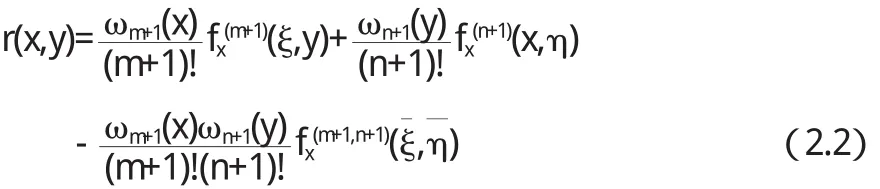
此处ξ和ξ¯落在包含x,x0,x1,…,xm的最小区间内,而η和η¯落在包含y,y0,y1,…,yn的最小区间内.
记Pm,n表示x与y的次数分别不超过m,n的二元多项式函数类.
定理2如果被插函数f(x,y)是属于Pm,n的二元代数多项式,则它在矩形网格…,n}上二元拉格朗日插值多项式就是它本身;有时也说插值是精确的.

是一个二元有理函数,且满足插值条件r(xi,yj)=fij,(i=0,1,…,m, j=0,1,…,n)但是(2.3)的缺点是二元有理插值函数的次数较高.
设qij≠0(i=0,1,…,m,j=0,1,…,n)是二元多项式

在矩形网格∏m,n={(xi,yj)/(xi,yj)∈R2,i=0,1…,m,j=0,1,…,n}上的函数值.其中s≤m,t≤n的正整数.

定理3对所有属于Pm,n二元多项式q(x,y),由式(2.5)给出的r(x,y)满足插值条件r(xi,yj)=fij,(i=0,1,…,m,j=0,1,…,n).
设fijqij≠0,i=0,1,…,m,j=0,1,…,n是二元多项式
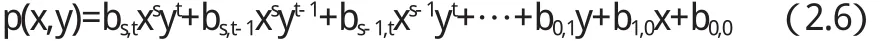
在矩形网格∏m,n={(xi,yj)/(xi,yj)∈R2,i=0,1…,m,j=0,1,…,n}上的函数值.其中s≤m,t≤n的正整数.
根据定理2,显然r(x,y)是次数较低的二元有理分式函数.则

定理4对所有属于Pm,n的二元多项式q(x,y),由式(2.7)给出的r(x,y)满足插值条件r(xi,yj)=fij,i=0,1,…,m,j=0,1,…,n.
式(2.5)和(2.7)就是给出的一般二元有理插值公式.通过选取次数较低的多项式q(x,y)或p(x,y)可以得到不同的次数类型的有理插值函数;且相比文[2]具有下列优点:
(1)文[5]中的有理函数的分母多项式是唯一确定的,而本文(2.5)的分母多项式可以是在矩形网格∏m,n={(xi,yj)/(xi,yj)∈R2,i=0,1…,m,j=0,1,…,n}处函数值不为零的任意属于Pm,n的二元代数多项式;
(2)文[5]中计算分母多项式需要很大的计算量,而本文是直接给出来的显示表达式;
式中:Td2和Td3的力矩值由曲线形上升段的半径所决定,即设计该助力特性曲线时,需要先根据实际需求给出曲线段特性曲线的函数表达式f(Td-Td2),然后以此为基础设定两直线段的斜率k1和k2,最后得出整段特性曲线的表达式.图11为根据改进后的特性曲线绘制出的三维曲面图.
(3)文[5]中计算分子多项式需要计算(m-d1)(n-d2)个二元插值多项式pi,j=(x,y),需要很大的计算量,而本文只需要计算一个二元拉格朗日插值多项式;
(4)文[5]中的方法只可以通过选取不同的正整数d1,d2,来降低分母多项式的次数,而本文既可以降低分母多项式的次数又可降低分子多项式的次数;
(5)文[5]中的方法对于不同的正整数d1,d2,需要重新计算pi,j=(x,y)和μi,j=(x,y);而本文无论分母多项式次数是多少,分子多项式中的基函数li(x)lj(y)始终不变,同样减少了较大的计算量.
本文的二元有理插值公式同样可以推广到二元向量值有理插值函数的情形,相比于文[5]中的方法同样具有上面的五个优点.
3 数值例子
例1[1]给定∏2,2及函数值f(xi,yj)如下表所示

x0=0x1=1x2=2 y0=0660 y1=1666 y2=2664
解法1用通常的分叉连分式插值方法是不可行的(因为逆差商为零).用[1]中的复合连分式的算法得到的二元有理插值函数为:
解法2取分母多项式y的次数全为零,按文[5]中的方法如下:
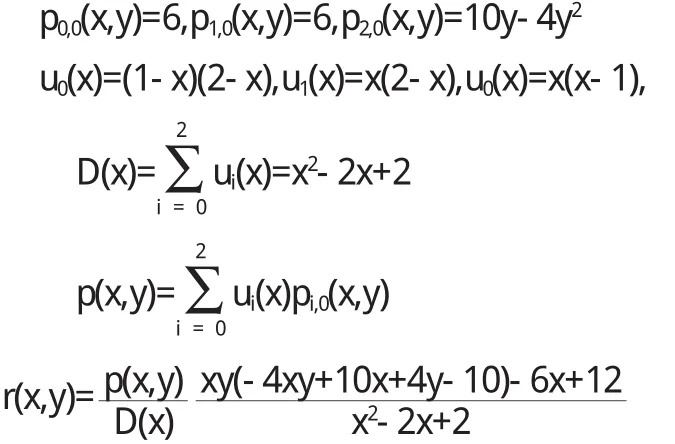
解法3取q(x,y)=x2-2x+2,那么q0,0=2,q1,0=1,q2,0=2,q0,1=2,q1,1=1,q2,1=2,q0,2=1,q2,2=2,
l0(x)=(x2-3x+2)/2,l1(x)=(2x-x2),l2(x)=(x2-x)/2
l0(y)=(y2-3y+2)/2,l1(y)=(2y-y2),l2(y)=(y2-y)/2
分子多项式为:

比较解法2和解法3,可以看出解法3比解法2更简便且计算结果完全一样.
〔1〕檀结庆,等.连分式理论及其应用[M].北京:科学出版社,2007.
〔2〕朱晓临.一种求二元有理插值函数的方法[J].大学数学,2003,19(1):90-95.
〔3〕荆科.构造有理插值函数的几种方法及其存在性的研究[D].合肥工业大学,2009.
〔4〕M.PolezziA.SriRanga.Onthedenominatorvaluesand barycentricweightsofrationalinterpolants[J].Journalof ComputationalandAppliedMathematics.2007,200: 576-590.
〔5〕朱功勤,郑林.矩形网格上的有理插值公式[J].自然科学进展,2009,19(5):520-525.
〔6〕王仁宏,梁学章.多元函数逼近[M].北京:科学出版社,1988.
〔7〕MichaelS.Floater,KaiHormann.Barycentricrationalinterpolationwithnopolesandhighratesofapproximation[J].NumerischeMathematik,2007,107:315-331.
O241.3
A
1673-260X(2013)03-0004-02
国家特色专业(数学与应用数学TS11496);阜阳师范学院科研项目(2012FSKJ07)

