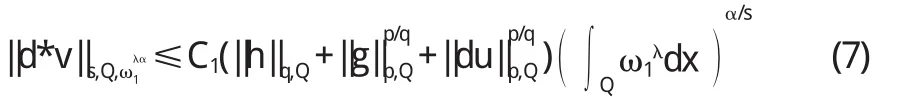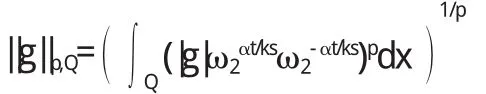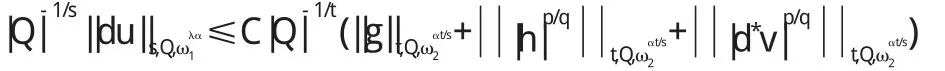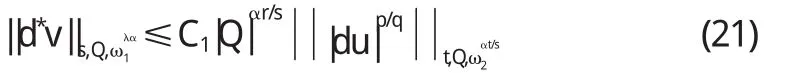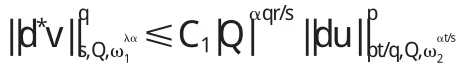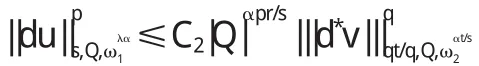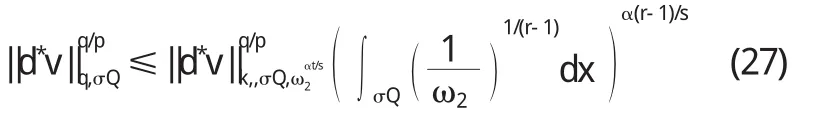共轭A-调和张量局部加权估计式
贺丹,金明浩
(黑龙江工程学院数学系,黑龙江哈尔滨150050)
共轭A-调和张量局部加权估计式
贺丹,金明浩
(黑龙江工程学院数学系,黑龙江哈尔滨150050)
本文将给出非齐次A-调和方程A(x,g+du)=h+d*v及共轭A-调和方程A(x,du)=d*v解的局部加权范数估计式.首先回顾了要用到的两个引理和A,(λ,Ω)-权函数的定义,并在这两个引理的基础上,给出了加A,(λ,Ω)-权的局部积分估计式.
非齐次A-调和方程;微分形式;双权函数;积分不等式
近年来,非齐次A-调和方程的理论研究取得了很大进展,C.A.Nolder[1]证明了非齐次A-调和方程解的可积性等.本文将给出非齐次A-调和方程

及共轭A-调和方程

解的局部加权范数估计式.
引理1设u和v是非齐次A-调和方程(1)在Ω上的解,如果g∈Lp(Q,Λl),h∈Lq(Q,Λl),那么du∈Lp(Q,Λl)当且仅当d*v∈Lq(Q,Λl),而且存在不依赖于u和v的常数C1、C2,使得对所有的球Q,若Q⊂Ω,则有

引理2设u和v是非齐次A-调和方程(1)在Ω上的解,则存在不依赖于u和v的常数C,使得对所有的球Q,若σQ⊂Ω,有

这里σ是一常数且σ>1.
定义1称权(ω1(x),ω2(x))满足Ar(λ,Ω)条件,r>1,λ>0,记为(ω1(x),ω2(x))∈Ar(λ,Ω),如果对任意的球体Q⊂Ω,满足

定理1设u和v是非齐次A-调和方程(1)在Ω上的解,(ω1(x),ω2(x))∈Ar(λ,Ω),r>1,那么存在一不依赖于u和v的常数C,使得对所有的球Q,若Q⊂Ω,有
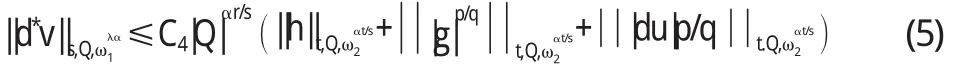
证明由于s=(1-α)q 综合(10)与(11)有 类似地,可得 综合(6)与(7),便有 把(8)、(12)、(13)代入(14)中,便得 由于(ω1(x),ω2(x))∈Ar(λ,Ω),于是 把(16)代入(15)便有 证毕. 采用相同的方法,可以得出关于du的Ls-加权估计. 定理2设u和v是非齐次A-调和方程(1)在Ω上的解,(ω1(x),ω2(x))∈Ar(λ,Ω),r>1,那么存在不依赖于u和v的常数C,使得对所有的球体Q,若Q⊂Ω,有 1.9 统计学处理 采用 SPSS 20.0 软件进行数据处理。呈正态分布的计量资料以±s 表示,两组间比较采用两样本均数比较的 t 检验(若方差不齐则采用 Welch 校正的 t 检验)。检验水准(α)为 0.05。 事实上,不等式(18)等价于 定理3设u和v是共轭A-调和方程(1-4)在Ω上的解,(ω1(x),ω2(x))∈Ar(λ,Ω),r>1,那么存在不依赖于u和c的常数C1与C2,使得对所有的满足Q⊂Ω的球体Q及任意的满足αr<1的正常数α,有 证明当g=0与h=0时,应用定理1可得 由计算可得 把(22)代入(21)可得 类似地,利用定理1在g=0、h=0时可得 定理4设u和v是共轭A-调和方程A(x,du)=d*v在Ω上的解,(ω1(x),ω2(x))∈Ar(λ,Ω),r>1,那么存在一不依赖于u和v的常数C1与C2,使得对所有的满足Q⊂Ω的球体Q及任意的满足αr<1的正常数α,有 证明应用推广的Hölder不等式及引理2有 由于 因此 经计算可得 综合(25)、(27)与(28),可得 由(ω1(x),ω2(x))∈Ar(λ,Ω)可得 把(30)代入(29)可得 (23)证明完毕,类似地可证(24). 〔1〕C.A.Nolder.GlobalIntegrabilityTheoremsforharmonicTensors.J.Math.Anal.Appl.2000,247:236~245. 〔2〕C.A.Nolder.Hardy-LittlewoodTheoremsforharmonicTensors.IllinoisJournalofMathematics.1999, 43:613~631. 〔3〕R.P.Agarwal,S.Ding.AdvancesinDifferentialForms andtheharmonicEquation.Math.Comput.Modelling. 2003,37(12-13):1393~1426. 〔4〕S.Ding,WeightedImbeddingharmonicTensors.PotentialAnalysis.2003,18:25~34. 〔5〕高红亚,陈银珠.A-调和方程弱解的逆Hölder不等式及其应用[J].应用数学,2002,15(4):102~104. 〔6〕S.Ding,C.A.Nolder.WeightedPoincaréInequalities forSolutionstoharmonicEquations.IllinoisJournalof Mathematics.2002,46(1):199~205. 〔7〕S.Ding,D.Sylvester.WeakReverseH?lderInequalities andImbeddingInequalitiesforSolutionstotheharmonicEquation.NonlinearAnal.TMA.2002,51(5): 783~800. 〔8〕冉启康.关于非齐次A-调和方程很弱解的合并问题[J].应用数学学报,2002,15(1):113~117. O175.2 A 1673-260X(2013)03-0001-03 黑龙江教育厅科学技术研究项目(12521457)