电磁兼容条件下的高功率因数PFC电路设计

赖龙龙，林维明

（福州大学电气工程与自动化学院，福建 福州350002）

0 引 言

随着电力电子设备的广泛使用，大量无功功率以及谐波电流被注入电网，由此引发的电网功率因数下降，电子设备受电磁干扰（EMI）的问题愈加严重。为此，各国对电子设备的功率因数（PF）、谐波含量以及电磁兼容性（EMC）做出了严格的限制，例如我国包括GB／T17626在内的电磁兼容相关标准体系以及国际电工委员会（IEC）发布的IEC61000、CISPR22等标准。因此，功率因数校正（PFC）以及EMI滤波器设计成为电子工程师在设计中必须考虑的问题［1，2］。

本文详细分析了EMI滤波器对PFC电路的影响，并在此基础上提出了采用BOOST型PFC电路时如何对EMI滤波器影响进行补偿的方法。

1 功率因数校正

功率因数（Power Factor，PF）是指设备的输入有功功率（P）与视在功率（S）之比，其值可由式（1）给出［3］。

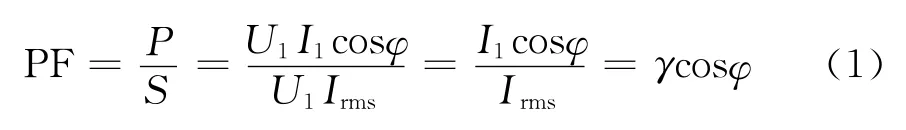
式中，U1为基波电压有效值；I1为基波电流有效值；φ为基波电流与基波电压相位差；Irms为输入电流有效值；γ＝I1／Irms为电流波形失真系数；cosφ为相移因子。

当输入电流波形失真而非正弦波时，定义输入电流的总谐波失真（Total Harmonic Distortion，THD）如式（2）所示［3］。

式中，In为第n次谐波电流有效值。将式（2）代入式（1）可得：

由式（3）可以看出，提高电子设备PF的方向有两个，即减小基波电流与基波电压相位差以及减小输入电流畸变。

接入电网的开关电源需要在前级对输入交流电进行整流，典型的桥式整流电路及其输入电压电流波形如图1所示［3］。由于整流桥后储能电容的存在，整流桥二极管仅在输入电压尖峰附近输入电压大于电容电压时才导通。因此输入电流形成如图1所示的尖峰电流，电流严重畸变致使PF下降。

图1 不控桥式整流及输入电压电流波形图

有源功率因数校正技术（Active Power Factor C－orrect，APFC），通过使电路中有源开关器件以高频通断的形式工作，可以使输入电流跟踪输入电压，从而实现提高功率因数，降低THD的目的。以Boost型PFC电路为例，其拓扑及其工作于BCM模式时输入电压电流波形如图2所示［4］。

图2 临界连续BOOST型PFC电路

2 EMI滤波器

电磁兼容（Electro Magnetic Compatibility，EMC）设计包括两个方面的内容，一是电子设备能够在一定的电磁干扰（Electro Magnetic Interference，EMI）条件下正常工作，即对电磁干扰有一定抗扰度；二是电子设备所发出的电磁骚扰信号被控制在一定的范围之内。电磁干扰信号按频率不同被分为传导干扰和辐射干扰，150 kHz至30 MHz频段为传导干扰，30 MHz至300 MHz为辐射干扰。传导干扰沿电源线传播，分为差模干扰和共模干扰。共模干扰信号由L线、N线共同进入，经地线回到电源；差模干扰则在L线和N线之间流动［5］。

开关电源中为了抑制传导干扰，需要在电源输入端加入共模和差模滤波器件。典型输入滤波电路如图3所示［5］，共模电感LY与共模电容 CY1、CY2构成共模滤波器，Cx与整流桥后π型滤波器C1、L1、C2共同构成差模滤波器。

3 差模滤波对APFC影响分析

图3 输入滤波电路

共模电感对于差模输入信号近似为零阻抗，在分析中仅考虑整流桥前差模电容、共模电感的漏感以及桥后π型滤波器对于PFC电路的影响。此外，在有源功率因数校正中通过控制芯片能够实现PFC部分输入电流完全跟踪输入电压，因此在分析中可以将PFC部分等效成电阻进行分析。

当不考虑EMC时，BOOST型PFC电路如图2所示。桥后的电容用于滤除由于开关造成的高频纹波，使输入电流平滑。电容的取值由式（4）给出［6］，此时电容仅用于滤除开关纹波，电容取值相对考虑EMC时要小的多，因此可以很容易的提高PF。此时输入电压和输入电流波形与不控整流相同，但由于C0很小，导通角接近π／2，故而PF更高。

式中，Iin为对应最小输入电压时的输入电流；fmin为PFC最小工作频率；r为C0电压纹波系数；Uacmin为最小输入电压。

当考虑EMC，在桥前加入差模电容，桥后加入π型滤波器时BOOST型PFC电路如图4所示。对PFC级进行等效，得到等效电路图如图5所示。图5所示电路输入电压输入电流波形如图6所示。

图4 加差模滤波BOOST型PFC电路

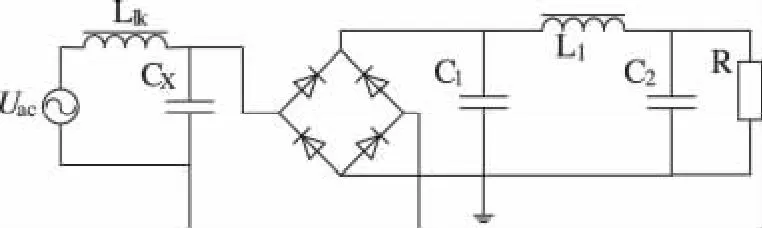
图5 加差模滤波BOOST型PFC电路等效仿真图

图6 经差模滤波及PFC电路校正输入电压电流波形

t0－t1：输入电压大于C1端电压，二极管 D1、D4导通，D2、D3截止，输入电流通过整流桥及π型滤波器流向负载。此时，输入直接给 Llk、Cx、C1、L1、C2以及 R构成的容性负载阻抗网络供电，输入电流超前输入电压，超前角为φ。

t1－t2：输入电流反向变负，二极管 D1、D4导通，D2、D3截止。此时电容Cx放电，电流分两路，一路流向输入端使输入电流反向，另一路通过D1、D4流向负载。

t2－t3：输入电压小于 C1端电压，二极管 D1、D4、D2、D3均截止。输入电流等于电容Cx放电电流。电容C1、C2放电，电流流向负载R，电容电压下降。至t3时输入电压大于C1端电压二极管D2、D3导通，D1、D4截止。t2至t3时刻整流桥截止，输入电压不向负载供电，输入电流畸变，β角、θ角为畸变角。

后半周期与前半周期类似，输入电流反向，本文不再展开讨论。从图6中可以看出，EMC滤波器的加入使输入电流波形严重畸变，PF值下降。桥前X电容及桥后π型滤波器中的电容使得电路输入阻抗呈容性，输入电流超前输入电压。

4 高功率因数滤波电路设计

对于图（6）中的超前相位角φ和畸变角β和θ，可以通过计算负载阻抗网络的阻抗角得出。在计算中忽略2次及2次以上纹波。

超前相位角φ可由式（5）给出。φ角是Llk、Cx、C1、L1、C2以及R构成的容性负载阻抗网络的阻抗角。

式中，ω为输入电压角频率，对于我国市电ω＝2πf＝2×3．14×50 rad／s＝314 rad／s。R 为负载等效电阻，其值可由 R＝Urms－in2／PPFC－in给出，Urms－in为输入交流电压有效值，PPFC－in为PFC级输入功率。

由式（3）和式（5）不难推出，PF随输入电压有效值和频率的上升而下降，随PFC输入功率的上升而上升。

对于β角的计算，可由式（6）给出。β角即为桥后π型滤波器与负载R组成的阻抗网络的阻抗角。

由图6可知，t0时刻前整流桥截止，在输入电压大于C1端电压后重新导通，这个过程相当于一个整流桥后带滤波电容的不控整流过程。此时θ角即为起始导电角，可由式（7）给出［3］。从式中可以看出，θ角随Rω（C1＋C2）的增大而增大。

从上述分析可知，EMC滤波器的引入使输入电流的相位角超前输入电压，输入电流波形产生畸变。为了提高功率因数，降低THD，应减小超前角φ，减小畸变角β和θ。据此，可以推出在综合考虑EMC和PFC时差模电容的两条设计原则：

原则一：在能满足EMC的前提下可以考虑增大差模电感的使用，尽量减小Cx＋C1＋C2的大小；

原则二：β角、θ角均随Rω（C1＋C2）的增大而增大，因此在保证Cx＋C1＋C2大小的前提下，Cx和C1＋C2的配合中，可以考虑增大Cx，减小C1＋C2，但C1＋C2的取值要大于式（4）中C0的值。

5 PFC补偿电路设计

第4节分析了如何设计Cx、C1、C2以保证在满足EMC的条件下尽可能的提高PF，减小THD。本节将分析在Cx、C1、C2已定的情况下，如何在PFC级中通过电路补偿，以减小超前相位和增大导通角，提高PF减小THD。

由式（5）、式（6）和式（7）可知，在输入电压过零点附近出现的φ、β、θ三个角均随负载R的增大而增大。在第3节的分析中均假设R值在整个周期中固定不变，但分析可知，如果使R在过零点处减小（即负载电流增大），在峰值处变大（即负载电流减小），整个周期内电流的平均值不变，则有可能使PF和THD得到改善。而定性分析的结果也是一样的，当过零点处负载电流变大时，C1、C2上的最低电压相应减小，整流桥的导通时间变长，电流畸变减小，PF和THD得到改善。因此，本节将重点讨论如何增大过零点负载电流，进行过零点失真补偿。

本文以临界过渡模式PFC控制芯片L6563［7］为例介绍PFC的电路补偿。如图7所示，L6563的MULT脚和INV脚分别是乘法器的输入端和误差放大器的反向输入端。MULT脚是L6563乘法器的输入端，整流桥后的电压波形经分压后被送入MULT脚，经乘法器用于提供电流波形基准。MULT脚的电平高则输出的峰值电流大。INV脚是PFC输出电压环误差放大器的反向输入引脚。通过调节INV上的分压电阻，可以调节PFC输出电压的大小。电压环的误差放大输出被送到乘法器用于调节电流参考基准。本文讨论的几种补偿方案正是建立在这两个引脚上的。

图7 L6563应用图

方案1是通过MULT脚进行补偿。如图8通过在MULT脚的分压电阻处增加一个稳压管ZD1，可以有效的对PFC电路进行过零补偿［8］。当整流线电压在峰值附近时MULT脚的电平被稳压管箝位，输入到乘法器的电平减小，而使得峰值附近电流减小，为维持输出功率过零点附近的电流就相应增大，从而达到增大过零点负载电流的目的，进而使PF得到提高。

方案2如图8所示，在MULT脚的下分压电阻处并一电容，使MULT脚电平滞后于整流线电压。当输入电压过零时，MULT脚电平不在谷底，从而增大过零点电流。通过调节下分压电阻和电容，可以有效地补偿过零点失真，提高PF降低THD。

图8 L6563补偿方案

方案3是通过INV脚进行补尝。通过向INV脚注入与整流桥后电压同相位的电压，可以使误差放大输出在电压尖峰附件减小，而在谷底附近加大。误差放大信号注入乘法器后就可以使输出电流在电压尖峰附近减小，在谷底附近增大，因此可以提高PF降低THD。

6 实验结果

根据上述分析，本文制作了一台基于L6563控制的150 W实验样机。设计参数：输入90～305 Vacrms，PFC级输出功率155 W，输出电压450 V。设计PFC电感为380μH。

图9为不同差模电感和差模电容组合下样机在220 Vac－rms满载时的传导干扰曲线。从图中可以看出，在3种组合下传导干扰曲线无太大变化。而从表1可以看出组合2和组合3的PF和THD则明显要优于组合1。实验结果证明了第4节中推出的两条设计原则的正确性。

图9 不同差模滤波组合的传导干扰图

表1 不同差模滤波组合的PF和THD对比

表2为采用3种不同补偿方案时的PF和THD与未采用补偿时的对比。从中可以看出第5节中所述的3种补偿方案能够有效的提高PF减小THD，证明了理论分析的正确性。

表2 不同补偿方案的PF和THD对比

此外，图10对未补偿和采用补偿方案2时的输入电流、输入电压与C1端电压的波形进行了比较。从图中可以看出，采用补偿方案2时C1在输入电压过零点时，最小端电压从64 V变为58 V，而整流桥截止时间由1．6 ms变为1．4 ms，畸变角减小。这与理论分析是一致的。

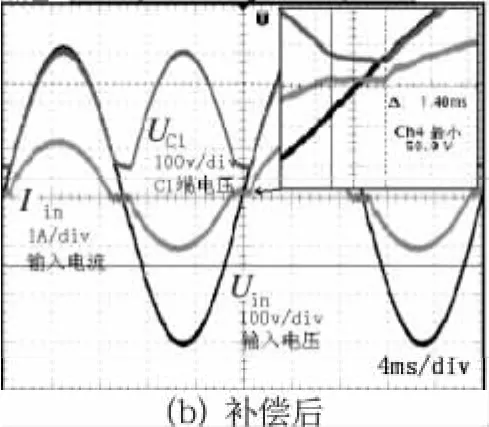
图10 补偿前后输入波形对比

7 结 论

本文详细分析了差模滤波电路对输入电流的影响，比较了不同输入差模滤波电路下的PF和THD，并推导出了差模滤波设计中的两条原则，同时介绍了PFC电路的补偿原则与几种常见的补偿方案。最后，文中制作了一台150 W的实验样机，实验结果证明了理论分析的正确性。合理设计差模滤波器，采用适当的补偿电路能够有效的改善PFC电路性能，提高PF降低THD。

［1］ MM Jovanovic，D E Crow．Merits and limitations of fullbridge rectifier with LC filter in meeting IEC 10002322 harmonic 2limit specifications［J］．IEEE Trans．on Industry Applications，1997，33（2）：5512557．

［2］ 林维明，宋辉淇，华晓辉，等．新电磁兼容标准条件下的功率因数校正电路的设计分析［J］．电工电能新技术，2006，25（2）：11－14．

［3］ 陈 坚．电力电子学［M］．北京：高等教育出版社，2004．

［4］ 周志敏，周纪海．开关电源功率因数校正电路设计与应用［M］．北京：人民邮电出版社，2004．

［5］ 钱照明，程肇基．电力电子系统电磁兼容设计基础及干扰抑制技术［M］．杭州：浙江大学出版社，2000．

［6］ 张振银．200 WLED驱动电源研究［D］．杭州：杭州电子科技大学硕士学位论文，2008．

［7］ L6563，datasheet．http：／／www．st．com／internet／com／TECHNICAL＿RESOURCES／TECHNICAL＿LITERATURE／DATASHEET／CD00003316．pdf．

［8］ 皇家菲利浦电子有限公司．功率因数校正电路［P］．中国，00800769．12000，4．27．