外加磁场下类氢施主杂质量子点中的激子

黄锦胜，林少光，林凯燕，陈国贵



外加磁场下类氢施主杂质量子点中的激子

黄锦胜，林少光，林凯燕，陈国贵

（揭阳职业技术学院 师范教育系，广东 揭阳 522051）

利用精确对角化方法计算了外加磁场下类氢施主杂质量子点中的激子的束缚能，发现系统的束缚能随着量子点的束缚势的增大而减小，随着外加磁场的增大而减小.

类氢施主杂质；量子点；磁场；束缚能

1 理论推导

引入二维谐振子波函数乘积基：

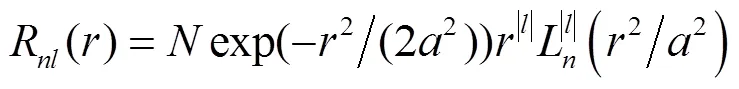
2 计算结果和讨论

本文着重考查束缚态的存在会受到哪些条件的影响. 参照文献[17]束缚能表示为

其中，是杂质系统激子的本征能量，是空穴在抛物势量子点中的最低能量，其不受库仑势作用，是杂质束缚着电子的基态能. 从式(6)可以看出，束缚能就是把空穴从杂质系统内激子的束缚态中分离出来，成为在量子点中具有基态能为的单粒子态所需的最低能量. 当时，激子在杂质系统存在束缚态.

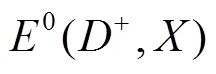
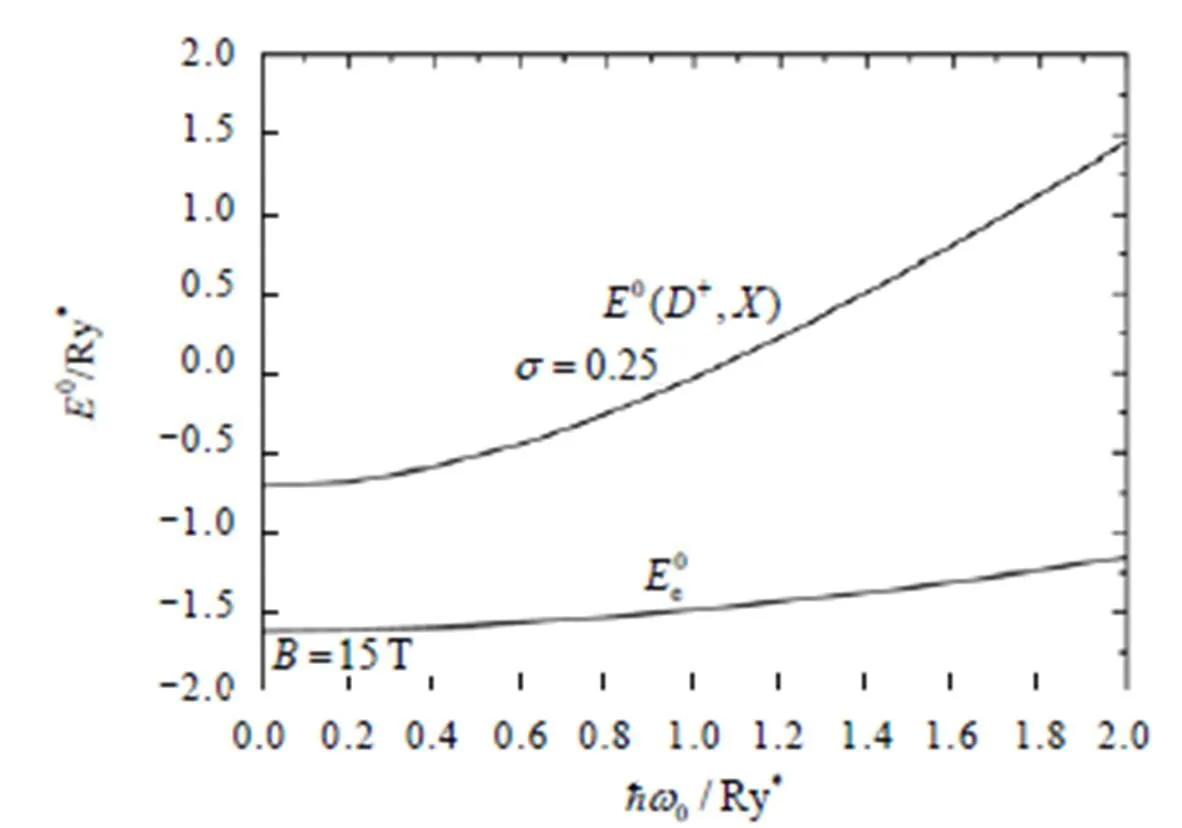
图2 施主杂质系统中激子基态能和电子基态能随束缚势大小的变化关系

图3 施主杂质系统中激子基态(L=0)和第一激发态(L=1)束缚能随外加磁场大小的变化关系

图4 施主杂质系统中激子基态束缚能随电子空穴质量比大小的变化关系

3 结论

[1] JACAK L, HAWRYLAK P, WOJS A. Quantum Dots [M]. First Version. Berlin: Springer, 1998: 5-12.

[2] YOFFE A D. Semiconductor quantum dots and related systems: electronic, optical, luminescence and related properties of low dimensional systems [J]. Adv Phys, 2001, 50(1): 1-208.

[3] BROZAK G, MCCOMBE B D. Potential and magnetic field confinement of shallow donor impurities in semiconductor quantum wells [J]. Phys Rev B, 1989, 40(2): 1265-1270.

[4] KASAPOGLU E, SARI H, SOKMEN I. Binding energies of shallow donor impurities in different shaped quantum wells under an applied electric field [J]. Physica B, 2003, 339(1): 17-22.

[5] KASAPOGLU E, SOKMEN I. Shallow donor impurity binding energy in the V-shaped quantum well under the crossed electric and magnetic fields [J]. Physica E, 2005, 27(1-2): 198-203.

[6] KASAPOGLU E, SARI H, SOKMEN I. Geometrical effects on shallow donor impurities in quantum wires [J]. Physica E, 2003, 19(4): 332-335.

[7] VARSHNI Y P. Binding energy of a screened donor in a spherical quantum dot with a parabolic potential [J]. Superlattices and Microstructures, 2001, 29(3): 233-238.

[8] GOMEZ S S, ROMERO R H. Binding energy of an off-center shallow donor D- in a spherical quantum dot [J]. physica E,2010, 42(5): 1563-1566.

[9] ZENG Zaiping, GAROUFALIS C S, BASKOUTAS S, et al. Stark effect of donor binding energy in a self-assembled GaAs quantum dot subjected to a tilted electric field [J]. Phys Lett A, 2012, 376(42-43): 2712-2716.

[10] XIE Wenfang, GU Juan. Exciton bound to a neutral donor in parabolic quantum dots [J]. Phys Lett A, 2003, 312(5-6): 385-390.

[11] BASKOUTAS S, SCHOMMERS W, TERZIS A F, et al. Stability of an exciton bound to an ionized donor in quantum dots [J]. Phy Lett A, 2003, 308(2-3): 219-225.

[12] SKETTRUP T, SUFFCZYNSKI M, GORZKOWSKI W. Properties of excitons bound to ionized donors [J]. Phys Rev B, 1971, 4(2): 512-517.

[13] STAUFFER L, STÉBÉ B. Binding energy of ionized-donor-bound excitons in two-dimensional semiconductors [J]. Phys Rev B, 1989, 39(8): 5345-5348.

[14] RUAN Wenying, CHANG Yia-chung, Stability of ion-bound excitons in two dimensions [J]. Phys Rev B, 2002, 66(11): 115-314.

[15] STÉBÉ B, ASSAID E, Dujardin F, et al. Exciton bound to an ionized donor impurity in semiconductor spherical quantum dots [J]. Phys Rev B, 1996, 54(24): 17785-17793.

[16] GROOTE DE J J, HORNOS J E, COELHO H T, et al. Hyperspherical formulation of impurity-bound excitons in semiconductors [J]. Phys Rev B, 1992, 46(4): 2101-2108.

[17] XIE Wenfang, GU Juan. Binding energies of an exciton bound to a charged impurity in quantum dots [J]. Physica B, 2003, 337: 58-63.

[18] HUANG Jinsheng, XIE Wenfang. Positively charged exciton in double-layer quantum dots [J]. Commun Theor Phys, 2007, 48(2): 353-356.

[责任编辑：韦 韬]

Exciton of a Hydrogenic Donor Quantum Dot in a Magnetic Fields

HUANGJin-sheng, LINShao-guang, LINKai-yan, CHENGuo-gui

(Department of Normal-education, Jieyang Vocational Technology College, Jieyang 522051, China)

An investigation of binding energy of a hydrogenic donor in a parabolic quantum dot with exciton under magnetic field is calculated by using the matrix diagonalization method. The results indicate that the binding energy decreases with increasing confinement strength and also decreases with increasing the magnetic field strength.

Hydrogenic donor; Quantum dot; Magnetic field; Binding energy

1006-7302（2013）01-0050-05

O474

A

2012-10-09

揭阳职业技术学院重点资助项目（JYCKZ1102）

黄锦胜（1980—）, 男，广东梅州人, 讲师，硕士，主要从事低维半导体材料光学性质研究.