涉及分担值的亚纯函数族正规族

潘佛文，徐俊峰



涉及分担值的亚纯函数族正规族

潘佛文，徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

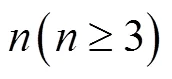
亚纯函数；正规族；微分多项式

1 引言及主要结果

首先介绍以下2个定义.

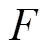
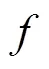
1959年，W. K. Hayman[3]证明了如下著名的结果.

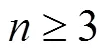
许多作者[5-10]研究了Hayman猜想，最终其被陈怀惠等[8]解决. 近年，利用分担值研究正规定则得到了大量关注[10-14]，如张庆彩[10]利用分担值对Hayman猜想进行推广并得到了如下结果.

2 相关引理

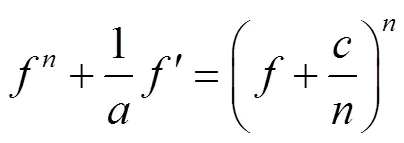
由式（2）有

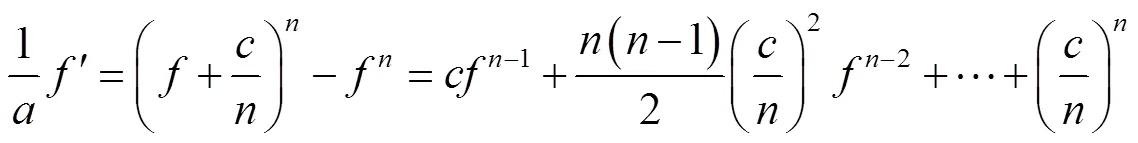
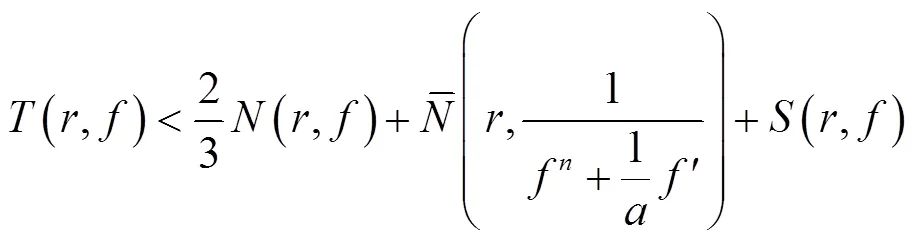
注意到

接下来，分2种情形进行讨论.

因此

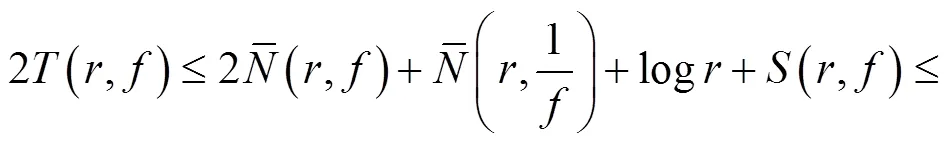
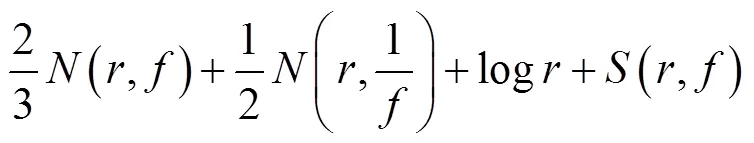
因此

3 定理1的证明

[1] YANG Lo. Value distribution theory [M]. Berlin: Springer-Verlag，1993.

[2] 仪洪勋，杨重骏. 亚纯函数惟一性理论[M]. 北京：科学出版社，1995.

[3] HAYMAN W K. Picard values of meromorphic functions and their derivatives [J]. Ann of Math, 1959, 70: 9-42.

[4] HAYMAN W K. Research problems in function theory [M]. London: Athlone Press, 1967.

[5] DRASIN D. Normal families and the Nevanlinna theory [J]. Acta Math, 1969, 122: 231-263.

[6] LANGLEY J K. On normal families and a result of Drasin [J]. Proc Royal Soc Edinburgh:Ser A, 1984, 98(3-4): 385-393.

[7] 杨乐. 正规族与微分多项式[J]. 中国科学：A辑，1983, 26: 21-32.

[9] 叶亚盛. 一个新的正规定则及其应用[J]. 数学年刊：A辑，1991, 12（增刊）：44-49.

[10] ZHANG Qingcai. Normal families of meromorphic functions concerning shared values [J]. J Math Anal Appl, 2008, 338(1): 545-551.

[11] 常建明. 与分担值有关的正规族[J]. 中国科学：A辑，2009，39(4): 399-404.

[12] 吕锋，徐俊峰，仪洪勋. 全纯函数的正规族[J]. 数学学报：中文版，2010, 53(5): 963-974.

[13] 徐俊峰. 全纯函数的正规族与分担集[J]. 五邑大学学报：自然科学版，2011, 25(1): 1-6.

[14] 顾永兴，庞学诚，方明亮. 正规族理论及其应用[M]. 北京：科学出版社，2007.

[15] PANG Xuecheng，ZALCMAN L. Normal families and shared values [J]. Bull London Math Soc, 2000, 32: 325-331.

[16] ZALCMAN L. Normal families [J]. New perspectives Bull Amer Math Soc, 1998, 35: 215-230.

[17] ZHANG Zhanliang, LI Wei. Tumura-Clunie’s theorem for differential polynomials [J]. Complex Variables, 1994, 25: 97-105.

[18] 仇惠玲，刘丹，方明亮. 涉及正规族与分担值的Hayman问题[J]. 中国科学：数学，2012, 42(6): 603-610.

[责任编辑：熊玉涛]

Normality Families of Meromorphic Functions Concerning Shared Values

PANGFo-wen, XUJun-feng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

meromorphic function; normal family; differential polynomials

1006-7302（2013）01-0016-05

O174.52

A

2012-10-19

国家自然科学基金资助项目（No. 11126327）；广东省自然科学基金资助项目（S2011010000735）

潘佛文（1989—），男，安徽安庆人，在读硕士生，研究方向为复分析及其应用；徐俊峰，副教授，博士，硕士生导师，通信作者，研究方向为复分析及其应用.