精细结构对分形天线小型化的影响
刘 成, 雷 虹, 何慧芬
(1.沈阳航空航天大学 辽宁 沈阳 110136;2.沈阳飞机设计研究所 辽宁 沈阳 110035)
无线通讯技术的飞速发展,通讯设备的小型化设计有了更高的要求,天线作为辐射和接收电磁波的重要媒介,也作为系统的最不可或缺的部分,则随着电子设备的发展趋势,也有着小型化的要求。
小型化天线是指天线在保证带宽不变的前提下,与具有相同带宽的天线的尺寸相比较小的天线。天线的小型化中,天线的尺寸指的是天线的三维尺寸,无论是在哪个维度缩减了天线的尺寸,都可认为天线实现了小型化的目的[1]。而通常所使用的普通天线,由于天线的性能与其波长尺寸有着紧密的联系,天线尺寸的改变,总会使天线的带宽、增益等技术指标发生改变,因此,天线要实现其小型化设计总体上是很困难的[2]。
分形技术是近些年出现的一种新型的天线小型化技术,由于分形技术所使用的分形结构具有自相似特性和空间填充性,使得在将其应用到天线的设计中后,所设计的天线不仅具有很好的小型化效果,而且,天线的各种指标也有可能变得更好[3]。
1 分形技术和分形天线
1975年,美籍法国数学家 B.Mandelbrot首次提出了分形(Fractal)的概念,其拉丁文原意为“破碎”,用来研究自然界中非线性科学里的不光滑、不规则的物体对象[4]。分形几何学是分形理论的最初始的形式,也是专门研究无限复杂但具有特定意义的自相似图形或结构的几何学。
20世纪80年代以来,电磁理论与分形结构之间相互作用的研究变得越来越多,可是直到1990年,D.L.Jaggard提出了分形电动力学,才正式确定了分形结构和电磁理论结合的新方向[5]。
分形天线,就是天线的几何结构是分形结构的天线,而分形结构,大都是通过迭代产生的具有较强的空间填充型和自相似性的几何结构。分形结构由于其整体与局部以及局部与局部之间具有较强的自相似性,是一种与标度无关的几何结构,在用于天线的设计后可以使天线具有多频和宽频特性;而其还具有的较强的空间填充性,可以在较小的空间内具有较长的几何长度,在用于天线设计后,可以相应的增加天线的电长度,从而降低天线的谐振频率,因此可以用作小型化天线的设计[6]。
目前,在天线的小型化设计中常用的分形结构有:树形分形曲线、Koch 曲线、Hilbert曲线,Peano 曲线、Minkowski曲线、3/2维曲线等。
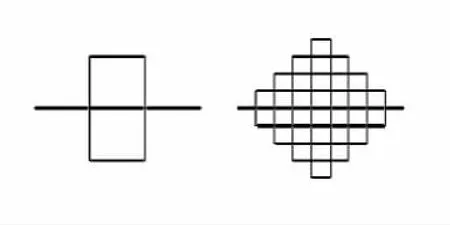
图1 Peano曲线Fig.1 Peano curve
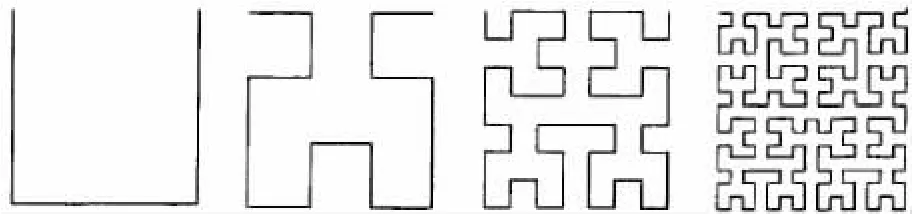
图2 Hilbert曲线Fig.2 Hilbert curve
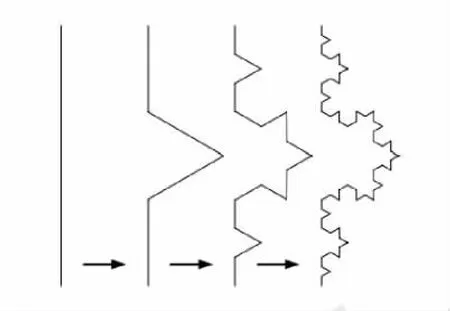
图3 Koch曲线Fig.3 Koch curve

图4 树形分形曲线Fig.4 Tree fractal curve
图1~图4所示的这些分形结构,在应用到天线的设计中后,都能够缩减天线的尺寸,尤其是Hilbert曲线,在应用到天线的小型化设计后,天线比例的缩减更是能做的很小(最大波长的1/10左右,甚至更小),而且天线的各种指标也未恶化。
2 精细结构对分形天线的影响
在分形天线中,精细结构指的是分形结构中最基础的分形单元,通常也就是指一阶分形结构,研究表明:精细结构的参数会对分形结构能否继续进行产生直接影响,继而对分形天线的小型化产生间接影响[7-11]。
图5所示的是普通单极子天线,在改变其结构的参数,即天线的高度(长度)h和宽度(直径)w后,所得的天线上电流分布的仿真示意图。
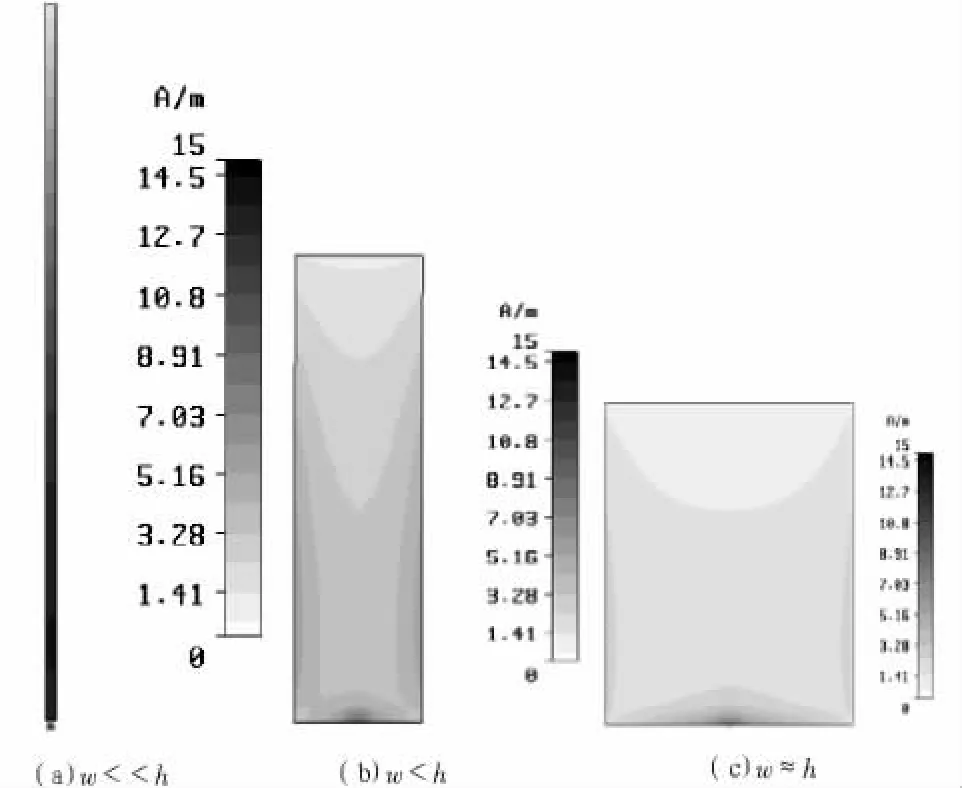
图5 普通单极子天线电流分布示意图Fig.5 Current distribution diagram of ordinary monopole antenna
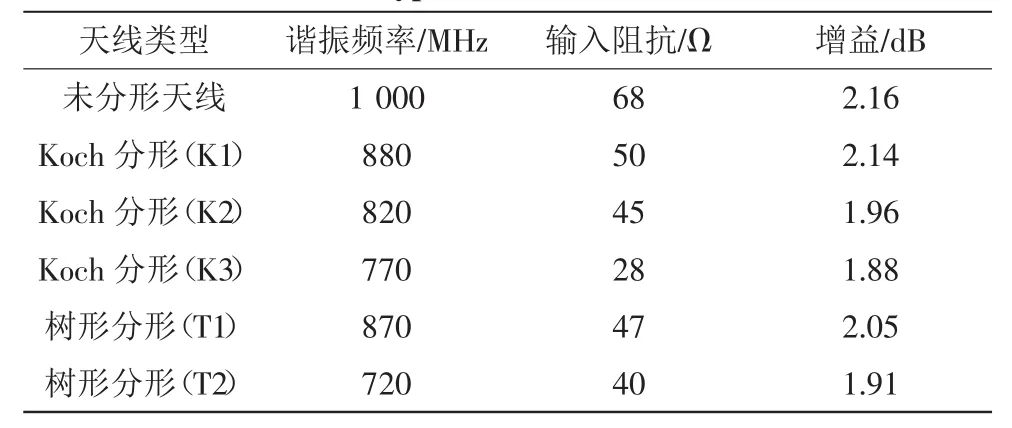
在图 5 中,图 5(a)、图 5(b)、图 5(c)所代表的分别是在保证天线的高度不变的基础上,改变天线的宽度,使其满足w< 而图6所示的是Koch曲线精细结构所设计的单极子天线,在改变天线的高度(长度)h和宽度(直径)w后,天线上电流分布的仿真示意图。 图6 Koch单极子天线电流分布示意图Fig.6 Current distribution diagram of Koch monopole antenna 这里,对Koch精细结构单极子天线,也作和普通单极子天线的情况相同的参数改变,就可以得到如图6(a)、图6(b)和图6(c)所示的仿真示意图。从仿真示意图可知,对于Koch分形天线,随着天线宽度的变宽,天线上电流的流动已不再是沿着天线的表面流动,在精细结构的结构尖锐处,天线的电流密度变得较大,而这种分布在尖锐结构处的较大电流,不仅会损耗较多的电磁能量,同时对天线主体的辐射也是不起太大作用的。 Koch分形天线精细结构的仿真分析表明,分形天线实现天线的小型化、缩减天线的尺寸是有一定的条件的,即如果精细结构的长度略小于或可比拟其直径时,再通过继续分形来获得谐振频率的降低或是尺寸缩减就没有意义了。 在实际中,应用分形天线进行天线的小型化设计时,常常的情况是一阶的分形结构并不能够达到所需的小型化要求,这时就需要使用高阶的分形结构去进行天线的设计,以达到所需的小型化要求。然而,到底需要使用多高阶数的分形结构去实现天线的小型化设计以及这种分形程度的分形结构能否实际做出都是要考虑的,这就使得必须要借助于精细结构,通过分析精细结构而得到。 表1为普通的偶极子天线、Koch分形对称振子天线 (一阶 K1、二阶 K2、三阶 K3)和树形分形对称振子天线(一阶T1、二阶T2)在相同的天线直径及相同横向天线尺寸的情况下,仿真所得的天线性能参数的比较表。 表1 不同类型天线的性能参数比较Tab.1 Comparison of performance parameters of different types of antennas 由表1中的天线参数可知,分形天线虽然能够降低天线的谐振频率、缩减天线的尺寸,而且高阶的分形天线也能比低阶的分形天线更大程度的缩减天线的尺寸,获得更好的天线的小型化效果,可是,这种每增加一阶分形结构所带来的天线的缩减效果却是越来越小的。 高阶的分形结构都是由低阶的分形结构继续分形所获得的,而由图1~图4所示的分形曲线的迭代图可知,分形结构每提高一阶,其分形结构的复杂程度就会迅速的增加,而一旦确定分形天线所能够使用的天线直径,高阶的分形结构就可能会迅速的达到精细结构的限定条件,从而使得继续分形下去没有了意义,而继续分形所得的分形结构在应用到天线中去也不能够再继续获得缩减天线尺寸的效果。 实际的天线,毕竟是一个三维结构,因此天线的直径不可能做到无限的细,总是有一个限度,而一旦确定这个限度,知道了天线的能够做到最小直径,就可以通过精细结构的研究确定所使用分形曲线能够达到的最大分形阶数,就可以通过仿真分析该分形曲线的较低阶天线的性能参数,去预估要获得所需小型化效果的分形天线的阶数或是确定使用该分形结构的天线是否能够设计出所需要求的小型化天线。 分形结构由于自身的自相似性及分形维特性,在用于天线的设计中后,能够获得性能参数较佳、小型化效果的很好的分形天线。精细结构的精细程度越精细,分形结构就能够进行越多次数的分形,分形天线小型化的程度也就越好,然而由于实际天线的三维特性,精细结构总会有一个下限,因此,对于一个特定的分形结构,用其设计成的分形天线的小型化程度也总是有一个上限,超过这个限度,就不能使用这个特定的分形结构,就需使用小型化程度更好的分形结构。而精细结构特性的研究,能够帮助确定分形天线所使用的分形结构的阶数,以及确定待使用的分形结构曲线能否满足所需的天线的小型化要求和应该使用什么样的分形曲线才能够满足所需的天线小型化要求,从而使分形天线的小型化设计做到未雨绸缪,事半功倍的效果。然而,由于分形技术、分形天线整体上,都还处于初级研究阶段,还有待我们进一步的研究。 [1]王琪.天线的小型化技术与宽频带特性的研究[D].电子科技大学,2004:53-71. [2]高建平,张芝贤.电波传播[M].西安:西北工业大学出版社,2002:280-288. [3]阮成礼,王春.小型化准分形加载单极子天线[J].电波科学学报,2006,21(5):727-730. RUAN Cheng-li,WANG Chun.A miniature quasi-fractal monopole loaded antenna[J].Chinese Journal of Ratio Science,2006,21(5):727-730. [4]Werner D H,Ganguly S.An overview of fractal antenna engineering research[J].IEEE Anlennasand Propagation Magazine,2003,45(1):38-57. [5]Sanchez J L.Experiences on Multiband Fractal Antennas[C]//Antennas and Propagation Society International Symposium,2001,4(4):58-61. [6]许峰.若干分形天线分析研究[D].西安:西安电子科技大学,2002:1-2. [7]林澍.小型化分型天线的设计[D].哈尔滨:哈尔滨工业大学,2008:35-41. [8]Puente C,Romeu J,Pous R,et al.Small but long Koch fractal monopole[J].IEE Electronics Letters,1998,34(1):9-10. [9]Werner D H,Suman,Ganguly.An overview of fractal antenna engineering research[J].IEEE Antennas and Propagation Magazine,2003,45(1):38-57. [10]杨跃胜,武岳山,熊立志,等.一种新型加载Sierpinski垫片天线的设计[J].现代电子技术,2010(21):76-78,82. YANG Yue-sheng,WU Yue-shan,XIONG Li-zhi,et al.Design of novel loaded sierpinski gasket antenna[J].Modern Electronics Technique,2010(21):76-78,82. [11]苏雪娟,杨岳,胡楠,等.改进型Sierpinski分形微带天线仿真[J].电子科技,2011(8):85-86. SU Xue-juan,YANG Yue,HU Nan,et al.The simulation of modified sierpinski fractal microstrip antenna[J].Electronic Science and Technology,2011(8):85-86.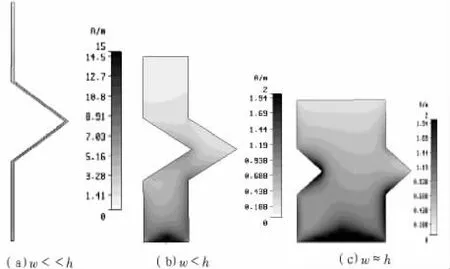
3 结 论

