基于聚类分析的警车巡逻方案的研究
周 媛,尹 乾,陈宁宁,高丽娜
(西安外事学院 工学院,陕西 西安 710077)
目前,在我国大中型城市的安全保卫基础工作中,110警车巡逻占据着不可或缺的地位。因此很多大中型城市都引入了警车巡逻的机制,安排若干辆警车在所辖范围内按照一定的方案巡逻。该机制不仅可以加快接处警(接受报警并赶往现场处理事件)时间,而且可以使警车以比较高的频率在市区内各个区域出现,从而在一定程度上对违法犯罪分子起到震慑作用,减少潜在案件的发生。然而,一个单位所拥有的警力资源却是相当有限的。因此,设计一种警车巡逻方案,使之能够在警车巡逻质量不变的情况下减少警车数量,是具有十分重要的实际意义的。换句话说,利用当前警车配备的较先进的定位和信息系统以及道路交通系统优化的思想和方法,制定一种较优的警车配置及巡逻方案对于社会安定具有至关重要的意义。针对这一重要问题,目前国内已有不少学者对此问题展开了研究[1-3]。
1 警车巡逻模型的建立
分析可知,警车的巡逻方案其本质就是对警车巡逻区域进行描述,也就是说其属于区域类划分问题,并且划分所得的区域还需要满足某些条件(如:接警后的到达时间)。因此,首先要解决的问题就是要确定合理的巡逻区域及划分方法,并依据一定的指标给出合理的巡逻方案。文中拟采用聚类分析[4]算法求解巡逻区域划分问题。在描述具体的模型之前,首先完成一些符号的定义作为模型的准备。
定义1:点到集合的聚类距离
d为点v到集合S的距离,如果d=max{d(v,vi)|∀vi∈S}。
定义 2:集合的直径
d为集合S的直径,当且仅当d=max{d(vi,vj)|∀vi,vj∈S}。
就目前国家安全部门的要求,警车在接警后3 min内赶到现场的比例不低于90%(下文中把该条件称为安全条件)。文中就以此要求为约束条件,设计警车数量最少的巡逻方案。在考虑110警车配置及巡逻方案时,若将事发现场抽象成一个点,巡逻道路抽象成一条直线,则在该直线上的每个点都有可能发生事故,这就要求所配置的110警车巡逻可控制的范围要能覆盖所有的道路。我们要做的就是在安全条件满足的情况下,使所需的警车配置数目的最小。也就是说,设法求该地区的一个划分,在每个划分区域中配置一辆警车。
因此,建立以划分的区域数目最少为目标的规划问题:
mink

其中k为划分的区域数目,并且要求该规划问题满足安全条件。
应用聚类分析的算法求解上述区域划分问题,这就要求该聚类算法的聚类标准能满足上述安全条件,同时聚类的区域要尽可能大。满足安全条件的聚类方案为:在所形成的非重点区域内,至少存在一个点,使得该点能在3 min内到达该区域内的其他点;在重点区域内,至少存在一个点,使得该点能在两分钟内到达该区域内的其特点。具体而言,对非重点区域,取尚未聚类的一些点为聚类的初始集合Si,任取剩余的未聚类的点 vj,计算其到 Si的聚类距离 dj,如果 dj<2·d3,则将 vj归入区域 Si,否则vj∉Si。 按此聚类标准,则在区域 Si中一定存在一个点,使得警车位于该点时均能按时到达该区域内的其他的点(最差情形下可取该类的外接圆,该圆的圆心就为所求的点)。类似的可以得到重点区域的聚类准则,只需更改点到该类的聚类距离的最大值小于2·d2即可。
由于在道路上的每个点都可能发生事故,所以应将道路上所有的点都进行聚类。但若将每个点都进行区域划分,这在实际情况中是无法完成的,而且原则上只要求警车赶到现场的比例不低于90%,故可只考虑道路交叉点的聚类问题。
v1和 v2是某段道路的两个端点,且 v1∈Si,v2∈Sj,但区域Si和Sj只覆盖了该段道路的一部分,道路段r1不属于任何区域,即警车无法在规定的时间内到达,最坏的情况为区域Si和Sj分别以v1和v2作为区域的端点,则v1和 v2整条道路都属于无人管辖区域。为了能够保证警车在非重点部位赶到现场的比例不低于90%,则警车不可能按时到达的所有道路长度总和不能超过所有道路长度总和的10%。因为该聚类方法是按照交叉路口点聚类的,所以各条道路中出现无人管辖的路段的概率相差不大,故可以用道路的平均长度来近似。又因为交叉路口处的道路可以近似认为是直线,所以可以假设相邻类别之间相互连通,且相连通的道路数为1,所以无人管辖的路段的个数可以近似认为是所划分区域的区域数。如果令道路的平均长度为x,分类数为n,所有道路的长度为l,则警车按时到达非重点部位的概率P≥1-。在不考虑重新加点的情况下,如果1-≥90%,则不要求再增加新的节点。否则,根据求得的分类数,计算出道路的平均值,从而得到需要增加的点数。
2 警车巡逻模型的求解
由上述的分析中可知,此问题的目标就是要求警车数量最少(即,划分区域的数目最小)和满足安全条件。假设所需的最小警车数为k,建立如下求解模型:

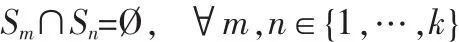
因为每一条道路上的每一点都可能发生事故,但若将所有道路上的所有点都进行聚类,这在实际中是无法办到的,故上述模型没有可以实现的解法。但根据问题分析,可以只对交叉路口进行划分,即将模型中的V转化成交叉路口点的集合V′。在聚类时,首先对重点部位进行聚类,以保证对于重点部位中的道路,警车能以100%的概率按时赶到。在对非重点部分进行聚类时,为了使该划分能尽可能多的覆盖这个地区,我们规定:距离已划分区域较近的点集优先聚类。
下面详述该模型的求解步骤:
Step0:V={v1,v2,…,vn}为要聚类的顶点集,d 为所要划分类别的直径的最大值。
Step1:设从该地区的某些顶点 v1,v2,…,vm开始聚类,令

Step2:判断某个点是否属于某个类。
任取vj∈V并标记 vj,根据定义 1,计算vj到类 Si的聚类距离dj。
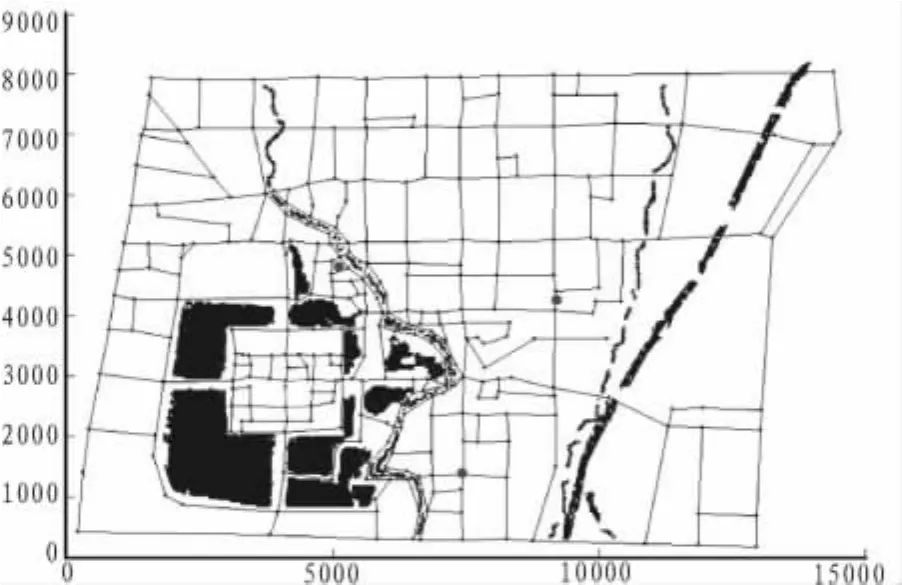
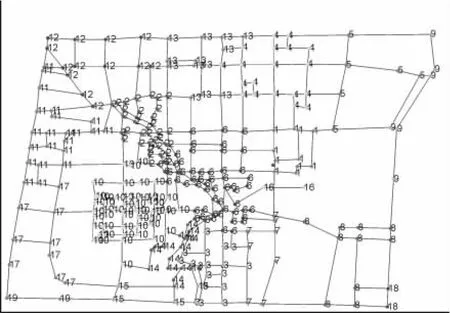
如果 dj Step3:如果V仍存在未标记的点,则循环step2;否则转到step4。 Step4:判断V是否为Ø,如果V≠Ø,则在所有不属于类Si的点中,选取到距离类 Si最近的一些点 vl,…,vs(l≤s),作为下一个类的初始集合,转到step2;否则算法停止,分类结束。 依据上述的分析可知,判断其是满足警车按时到达非重点部位的比例是否大于90%,如果是,则算法停止,否则按分析中给出的算法进行调整,直到满足条件为止。 图1给出了某城市的道路分布情况图,以该图为例,采用文中提出的算法进行求解。在求解时假设警车的平均巡逻速度为20 km/h,接警后的平均行驶速度为40 km/h。 图1 某市的道路分布图Fig.1 Road distribution map of a city 依据上述算法,得到如下的分类情形: 从图2中可以看出,该地区最少的分类区域数目为19(图中不同的数字所划分的不同区域),即满足安全条件时,该地区最少需要配置19辆警车巡逻,并由图2还可以看出文中算法得到的结果具有很强的定量化性质,其结果可以十分有效地对实际中警车的分配提供恰当准确的依据。 图2 最少警车配置图Fig.2 Minimum police car allocation graph 文中从警车巡逻这一实际问题出发,建立了警车巡逻的优化模型,提出了一种基于聚类分析的求解模型,用以解决这类问题。文中算法得到的结果完全符合现实应用需要,实现了警车巡逻的优化,可以有效的辅助公安部门制定合理高效的巡逻方案。 [1]甘若迅,吕睿,江一飞,等.基于遗传算法的警车巡逻问题求解[J].数学的实践与认识,2011,31(1):116-121. GAN Ruo-xun,LV Rui,JIANG Yi-fei,et al.Solution to police car patrolling problem based on genetic algorithm[J].Journal of Computer Applications,2011,31(1):116-121. [2]林阳斌,陈碧黎,苏圳泷.110警车配置及巡逻方案[J]. 数学的实践与认识,2010,40(15):185-193. LIN Yang-bin,CHEN Bi-li,SU Zhen-long.Distribution of 110 police wagon and the patrol scheme[J].Mathematics in Practice and Theory,2010,40(15):185-193. [3]李路,王行愚,江开忠.基于k阶不可逆邻接矩阵的警车巡逻[J].电气自动化,2010,32(4):32-34. LI Lu,WANG Xing-yu,JIANG Kai-zhong.Police cars patrol based on k-order irreversible adjacency matrix[J].Electrical Automation,2010,32(4):32-34. [4]边肇祺,张学工,等.模式识别[M].2版.北京:清华大学出版社,2000. [5]吴祈宗.运筹学与最优化方法[M].1版.北京:机械工业出版社,2008. [6]姜启源,谢金星,叶俊.数学模型[M].3版.北京:高等教育出版社,2010.3 模型结果分析
4 结束语

