高职数学闭环式教学模式的思考与研究

杨 菲

（天津市河西区职工大学，天津 300203）

高职教育，在层次上属于高等教育，在类型上是职业教育，培养的是技术型、技能型人才，也就是在生产和管理第一线从事全面技术性工作的人员。高等数学课程是高职教育必不可少的基础课程，数学教育是学习知识、提高能力和培养素质的统一体，数学的思想和方法在人们的学习和工作中发挥着潜移默化的作用，是任何一门学科所无法替代的。［1］数学学习可以培养学生严谨的处世态度，培养学生的创新能力，培养学生继续学习的能力。实践表明，在学生数学教育活动中有选择地运用操作学习，即理论联系实际，让学生在操作中主动地去探究、发现、验证，能在很大程度上促进其知识的增长、思维的发展和能力的提高，从而完善学生的大脑，造成大脑中新链接的形成。［2］因此，学生在数学学习中，不仅学会了数学知识，还掌握了数学的思想方法，学习潜力和创新能力也能够得到较大程度地挖掘，同时培养和提高了其继续学习、终身学习的能力。目前我国高职的数学教学实践仍然过分注重数学的基础知识的传授，漠视了数学思想方法和数学史蕴含的科学精神对学生的影响，影响了高职学生数学素养的培养和全面素质的提高。因此，探索一套适合高职的数学教学模式对于高职培养目标的实现有着重要的作用。

一、高职学生数学学习情况调查

（一）问题的提出

本研究基于问卷调查了解学生目前的数学学习状况、对数学应用的基本认识，进而研究高职数学课程的改革。

（二）调查对象及实施

学习高等数学的高职生，在第一学期高等数学讲授结束后对学生进行的问卷调查。

（三）结果与分析

1．关于学生数学学习情况的分析

高等数学是高职教育的基础课，对将来专业课的学习会起到一定的指导作用，教师会尽可能地系统地将高等数学中的重要知识传授给学生，但是从调查问卷的结果来看，只有9．52%的学生学习兴趣很浓，4．76%的学生学习兴趣浓，其他学生的学习兴趣不高；52．39%的学生认为数学课内容复杂、枯燥，方法繁琐难以理解；29．76%学生为了拿毕业证学习数学，38．1%的学生因为学校开设数学课而不得不学习数学，只有23．81%的学生认为学习数学是为了专业打好基础，从调查中可以分析得到大部分学生的数学学习较为吃力，学习主动性较差，总体的学习状况令人堪忧。即使数学教师很辛苦地进行解题步骤的讲解，但是学生的学习兴趣不足，越来越觉得数学学习枯燥无味。从这些可以看出，高职数学课程改革迫在眉睫。

2．关于学生数学思维能力的分析

从调查结果来看，超过半数的学生认为自己具备一定的数学思维能力，这是令人欣慰和可喜的结果，一是学生较为自信，二是学生在过去数学学习的过程中也获得了某方面一定的提高，这就为高等数学教学奠定了一定的基础。

3．关于学生对数学的作用认同度的分析

从调查结果中可以看出大多数的学生认为数学与自身的工作、日常生活、经济、计算机、哲学、教育有一定的关系，还可以看出在以前的数学教学中教师欠缺数学美、数学史的渗透。以后的数学课教学中16．67%的学生希望上课渗透数学史知识，26．19%的学生希望上课多联系日常生活知识，23．81%的学生介绍与本专业相关的数学知识，这些都表明学生对数学应用知识的渴望，从另外一个方面肯定了数学对其工作、生活、学习的作用。

二、闭环式教学模式的涵义

闭环控制是控制论的一个基本概念，指作为被控的输出以一定方式返回到作为控制的输入端，并对输入端施加控制影响的一种控制关系。［3］在控制论中，闭环通常指输出端通过“旁链”方式回馈到输入，输出端回馈到输入端并参与对输出端再控制，这才是闭环控制的目的，这种目的是通过反馈来实现的。从控制论的角度来看，任何一个教学系统，都应该是一个可控的闭环系统。高职数学教学同样应该是一个闭环系统，如图1所示。

图1 高职数学教学闭环系统

三、高职数学闭环式教学模式实现的对策思考

引入数学趣味题和渗透数学史可以激发学生的学习兴趣，结合专业实例能够促使学生掌握必要的数学知识，评价方式的改革促使学生数学素养的提高，从而提高学生的综合素质，而综合素质的提高又能进一步激发学生的学习兴趣，形成了如图1所示的闭环系统。

（一）引入数学趣味题，营造活跃的课堂气氛

学习兴趣的有无和强弱对学习的效果有很大的影响，如果要促进学生自主地学习数学，就必须激发和培养学生们的兴趣。一个有效的途径就是用趣味问题来激发学生的学习兴趣，使学生产生强烈的求知欲望，克服学生学习数学的厌倦心理，促进学生能有效地进行思维活动，营造活跃的课堂气氛。高职学生的数学基础较差，但是思维能力已接近成人水平，因此趣味题的选择应该难易适中，既不能太简单使学生觉得无聊，也不能太难使学生丧失自信心。以选择的一道趣味题为例：

甲和乙比赛100米冲刺，结果，甲领先10米到达终点。乙再和丙比赛100米冲刺，结果，乙领先10米取胜。现在甲和丙作同样的比赛，结果甲会领先多少米呢？

答案：如果你的答案是“甲领先20米取胜”，那就错了。甲和乙的速度之差是百分之十，乙和丙的速度之差也是百分之十，但以此得不出结论，甲和丙的速度之差是百分之二十。如果三个人在一起比赛，当甲到达终点时，乙落后甲的距离是100米的百分之十，即10米；而丙落后乙的距离是90米的百分之十，即9米。因此，如果甲和丙比赛，甲将领先19米。

这道题用到的计算简单但是考察的数学思维方法却很细致，这些就提示学生考虑问题的时候必须要具备一定的推理能力和计算能力，这些都是通过数学学习可以获得的，并且会对学生的日常生活和工作带来一定的影响，这必然会提高学生的数学学习兴趣，提高数学教学的效果。

（二）渗透数学史知识，营造良好的文化氛围

从20世纪70年代起，数学史在数学教育中的重要性逐渐为人们所认识，在20世纪70年代举行的几次国际数学教育会议上，曾开展过关于这方面的专题讨论，大家一致认为数学史对激发学生的学习兴趣有重要的作用。数学史，实际上是一部数学思想史，同时也是一部数学思维影响人的思想的历史，充分展示了数学知识产生、形成、发展的全过程，并展望知识发展的前景。通过联系数学史，可以使学生认识到，在数学领域任何一个定理的发现，都是前辈学者艰苦努力的结晶，数学知识的产生与自然客观的需求是分不开的。对数学史的介绍可以帮助学生了解数学创造的真实过程，使学生把握数学发展的脉络，加深对数学概念、思想方法的理解。如果教师能在数学教学活动中通过深挖数学知识的文化背景，充实他们的数学文化底蕴，将发现过程中活生生的数学“返璞归真”地教给学生，学生清楚地看到知识产生的原因，就能揭开数学神秘的面纱，消除学生对数学的畏惧感，使他们在内心深处亲近数学。

对于高职的高等数学教学，根据学生的学习水平较低的情况，在数学史的讲授中要注意小学、中学、大学知识的链接，以初等数学到高等数学的发展为时间主线，将数学史合理巧妙、恰如其分地渗透，循序渐进，给学生以知识调整的时间和过程，改变学生以前数学学习的恐惧感，培养学生的学习兴趣，建立学生学习高等数学课程知识的信心。

（三）贯穿数学与专业的关系，体现数学的应用价值

数学已广泛应用于自然科学、社会科学、管理科学等社会各个领域，成为这些领域的工具和语言。数学化，不仅仅是自然科学发展的趋势，而且是所有科学发展的趋势；不仅仅自然科学数学化，而且出现了社会科学数学化。［4］教师要与专业教师经常交流，深入专业了解情况，在教学中结合专业实例进行教学。［5］比如利用高等数学的知识可以分析商品的市场价格与需求量（供给量）之间的函数关系、经济最优化问题。下面讨论在物流经济中如何调配购货（或原材料）即订货批量与库存量之间的关系达到费用最省的问题。在一定的时期内，物资的总需求量一定时，订货批量大，订货次数就会减少，订货费用就会降低，然而保管费用会升高；若订货批量小，保管费用就会降低，而订货次数会增加，订货费用会升高。假定在一定时期内物资的总需求量为，每次的订货费用为S，单位物资在一定时期内的保管费用为C，订货批量为Q，则在瞬时到货方式下一定时期内保管费用为订货费用为总费用为Y＝Y1＋Y2，要使总费用最低，应用导数求最值的方法，解得利用数学知识建立模型以后，成功解决了许多经济问题。

因此，在对数学知识的讲解中，既要使学生掌握了经典的微积分知识，又介绍了专业相关的案例，让学生了解了学习目的，知道了学习的数学知识将来在专业学习中的作用，激发了学习兴趣，提高了学习效率。另外，在数学教学过程中贯穿数学在专业中的应用，并不意味着简单地将数学中的公式、定理、结论照搬，而是培养学生数学学习的思想和方法，能够在将来的专业课学习中较为熟练的运用数学知识解决专业问题，从而加深对专业问题的理解，真正做到理论联系实际。

（四）改革评价方式，形成闭环式的教学系统

学生数学素养的提高，不仅要依靠教师知识的传授，还要依靠学生主动的学习。以往的数学考核都是一纸定乾坤，学生的学习能力只限于对概念、结论的记忆与模仿上，这也就失去了数学课开设的意义。因此，高职数学教学改革的另一关键点就是要将多元化的评价方式运用到教学评价中，建立一套以“学生为本，学生为主体”的评价方式。笔者思考将考核内容分为三个部分，包括应用研究报告考核、演讲考核、期末笔试考核。应用研究报告是将学生分为小组，专业教师作为小组辅导教师，在教师的指导下利用数学模型来解决某些专业知识，在合作交流中解决问题，增进了同学间友谊，营造数学学习的氛围，最后形成小组的应用研究报告，并在最终考核成绩中占30%。演讲考核指的是学生根据本学期学习的数学知识和数学典故等内容写一篇学习体会论文，主要叙述数学对自身的影响以及学习数学后的自身感悟等，在课堂上演讲并在最终考核成绩中占30%，这种演讲是学生对学习的一种反思过程，并且能够锻炼学生的表达能力，从而提高学生的综合素质。［6］期末笔试考核的目的是督促学生掌握本学期学习的数学知识和数学运算方法，在最终考核成绩中占40%。学生数学评价方式及考核成绩如表1所示。

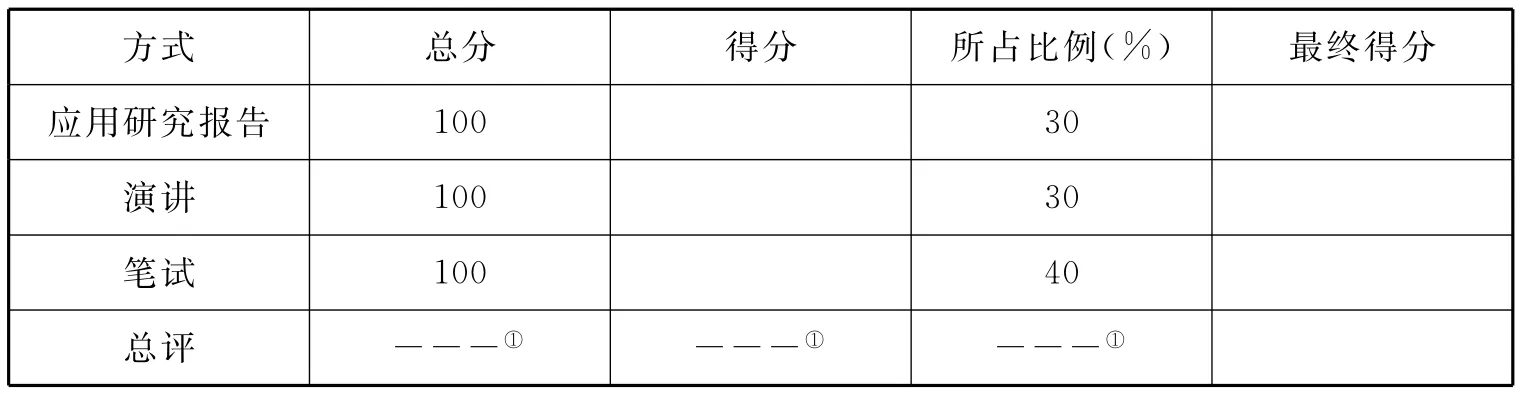
表1 高职数学考核成绩表

这种闭环式教学模式实施的目的不是检测学生数学学习是否合格，而是要通过这种模式的实施激发学生的学习兴趣，提高学生自主学习的能力，真正从数学学习中体会到数学的思想和方法，领悟到数学科学家不断探索创新、不惧困难的工作态度，从而提高自身的综合素质。综合素质的提高也必会进一步激发学生的学习兴趣，这种良性循环系统的实现也正是高职数学教学的最高目标。这些研究都是初步的，我们将在以后的教学中不断探索，不断改进教学内容和教学方法，为适应高职教育的发展而不懈努力。

［1］曾庆柏．高职数学课程体系改革研究［J］．中国职业技术教育，2008，（31）．

［2］张华．对高职高专院校数学教学的思考［J］．山西经济管理干部学院学报，2009，（02）．

［3］袁德成．现代控制理论［M］．北京：清华大学出版社，2007．

［4］丁石孙．张祖贵．数学与教育［M］．大连：大连理工大学出版社，2009．

［5］云连英．面向专业需求的高职数学课程设置研究［J］．数学教育学报，2008，（04）．

［6］陈丽华．数学反思学习的发展价值及其局限性［J］．教育学术月刊，2010，（04）．