准分子激光治疗设备光斑能量密度的可视化分析*

姜伟平 姚绍卫 张 超/ 江苏省计量科学研究院

0 引言

对于准分子激光治疗设备而言，手术端的光斑形状与激光能量密度是影响手术效果的最直接参数，对其进行准确辨识是评价准分子激光治疗设备的重要依据。LASIK 或LASEK 手术中，从激光出射到角膜消蚀完成，一般需要20～ 90 s的时间，视矫正的度数和准分子激光治疗设备的工作频率而定。激光出射后，因谐振腔内高压激励的热效应而导致腔内气体升温、粒子数反转浓度、腔内电子元器件稳定性等因素，会影响到激光光斑的能量密度。

由于激光的高单色性，用于判读的准分子激光光斑图像通常为灰度图像。人的眼睛虽然只能分辨少量不同的灰度级，但对色彩却相当敏感，能区分有不同亮度、色度和饱和度的成千上万种颜色。根据这个特点，可借助彩色化处理以得到对人眼来说增强了的视觉效果，提高光斑灰度图像的可鉴别性。一种常用的彩色增强方法，是对原来灰度图像中不同的灰度值区域赋予不同的颜色以更明显地区分他们。由于原图并没有颜色，所以人工赋予的颜色常称为伪彩色。因此，针对准分子激光治疗设备光斑能量密度的可视化分析，通过利用伪彩色变换和灰度插值运算，可以更加直观和清晰地分析激光光斑能量密度分布，从而为评价准分子治疗设备的性能提供参考依据。

1 伪彩色变换原理

伪彩色变换就是把图像的各个灰度值按一定的线性或非线性函数关系映射成相应的颜色，不同的灰度级对应不同的色彩。具体应用来说，灰度图像伪彩色处理的目的是为了得到对视觉效果更好、更有利于人眼辨识的图像。伪彩色变换不改变像素的几何位置，而仅仅改变其颜色，是一种很实用的图像增强技术。由于具体的应用和要求的不同，所需要的具体伪彩色变换方式也可以大不相同，可以有多种方式实现从灰度到彩色的变换。最简单的就是把灰度图像的灰度级别从0 到255 分成256 个区间，给每个区间指定一种色彩。此方法比较简单直观，缺点是变换出的色彩有限，表现力不强。

伪彩色变换的实现方法有多种，如密度分割法、灰度级-彩色变换法、滤波法等。其中，密度分割法是一种不连续的伪彩色处理方法，灰度级-彩色变换法则是一种连续的伪彩色处理技术，这两者都是空间域的伪彩色处理；而滤波法则是频率域的伪彩色处理技术。灰度级-彩色变换法更为通用，它能得到比密度分割法范围更宽的伪彩色增强效果。根据色度学原理，任何一种颜色都可以由红、绿、蓝三基色按不同的比例来合成。因此伪彩色处理首先要设定红、绿、蓝三个变换函数，对应每一个像素都有相应的红、绿、蓝输出，之后三者又合成一个颜色。其基本方法是在任何一个像素的灰度级上进行三个独立的变换，作为各自的三基色强度，用配色方程表示：

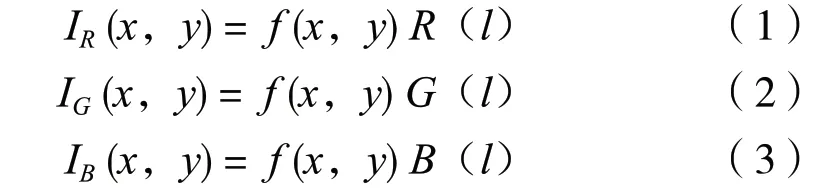
式中 ：f (x，y)—像素在坐标 (x，y) 处的灰度值；

R（l），G（l），B（l）—三基色变换函数；

IR(x，y) ，IG(x，y) ，IB(x，y)—变换后的三基色强度

把三基色强度信号单独送到R，G，B 三基色通道进行处理，合成产生一幅受变换函数所调制的伪彩色合成图像，f (x，y) 变换后的色彩表示为

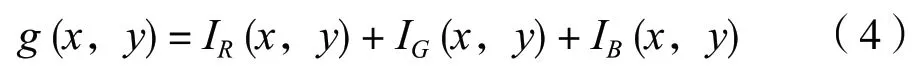
灰度级彩色变换方法使用的是光滑的非线性变换函数，变换函数常用取绝对值的正弦函数，其特点是在峰值处比较平缓而在低谷处比较尖锐。通过变换每个正弦波的相位和频率就可以改变相应灰度值所对应的颜色。当三个变换具有相同的相位和频率时，输出的图仍是灰度图；当三个变换间的相位发生一点微小变化时，其灰度值对应正弦函数峰值处的像素受到的影响较小，但其灰度值对应正弦函数低谷处的像素受到的影响较大，特别是在三个正弦函数均为低谷处，相位变化导致幅度变化更大。在三个正弦函数的数值变化剧烈处，像素变换后的色彩受灰度变化的影响最明显，不同灰度值范围的像素就得到了不同的伪彩色增强效果。

2 波面拟合

2.1 泽尼克多项式

镜面的波面一般趋于光滑和连续，所以可将镜面的面形变化表示成一个完备基底函数的线性组合或一个线性无关基底函数系的组合。利用多项式进行波面拟合非常方便，由于泽尼克多项式在连续的单位圆上正交，且自身具有旋转对称性，并与初级像差存在一定的对应关系，因此可使用泽尼克多项式对采集到的光斑进行波面拟合。单位圆上定义的泽尼克多项式在极坐标下的表达式为

式中：ρ—极轴；

θ—极角

m 和 n为整数，且有n -m=2p (p=0，1，2，…)，q 为模序列，且为m 和n的函数。

径向多项式Rnm定义为

根据式（8）即可计算出泽尼克多项式每项的表达式。

2.2 波面拟合算法

采用泽尼克多项式进行波面拟合，将被测波面用n 项泽尼克多项式表示为

对于m 个离散测量数据点 wi(xi，yi) (i=1，2，…，m)，令 aii=Zi(xi，yi) (i=1，2，…，n)，代入式（9）得到矛盾方程组：

将方程组(10)记为

其中：H=（aij）为 m×n 矩阵；

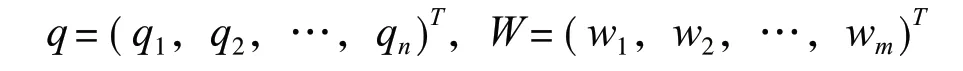
矛盾方程组式(11)一般不存在通常意义下的解，即对任何n 维向量 q，W -Hq≠ 0，此时用最小二乘法求解参数q1，q2，…，qn，可导出线性方程组：

式（12）即为求解最小二乘问题的方程组，求解此方程组即可得到q1～ qn，但在实际应用中，特别当处理的数据量较大时，为避免直接求解方程组，可以有两种方法：

1）以基底函数系为基础，通过交换函数族基底改变方程组状态，如Gram-Schmidt 正交法和协方差矩阵法；

2）不用构造法方程组，直接从矛盾方程组Hq=W开始，应用Householder 变换将系数矩阵正交三角化，从而求解。

3 激光光斑检测技术

激光光斑测量方法有机械扫描法和面阵CCD探测法等，实际检测中选择了以色列OPHIR 公司SP620U 型号的CCD 相机，并配备了1×UV Image Converter 和Optional Beam Splitter 附件用以衰减并转换193 nm的准分子激光为可见光入射相机进行分析（见图 1）。以面阵CCD 为探测器的检测技术具有响应时间快、可同时测量光束截面二维方向的能量密度分布等特性，并可以通过USB 接口和计算机进行数据通信，为进一步的图像处理分析提供光斑图像数据。

图1 检测中使用的SP620U 型号CCD 相机

4 准分子激光光斑伪彩色可视化

相对于二维图像，三维模型可以提供更全面和生动的信息表示。用计算机处理的光斑图像都是经过采样、量化和编码而生成的，在空间和灰度上均为离散化的数字图像。如果将这样的二维图像直接转换为三维显示，其效果并不理想。空间分布数据的插值是三维可视化过程中的重要环节，其性能将直接影响三维表示的质量。因此，将离散的空间分布数据形成合理的三维模型，首先必须进行数据的插值，然后才能进行可视化操作。

在数字图像中，其像素值仅在坐标值为整数处有定义，所以在非整数处的像素值要用其周围一些整数处的像素值计算，称为灰度插值。灰度插值的方法很多，最简单的是最近邻插值。最近邻插值就是将离非整数坐标(x，y)点最近像素的灰度值赋给图像中对应的点。这种方法的缺点是生成的图像粗糙，不易辨识；若提高样条插值的精度，则计算量大，处理时间长。双线性插值是一种较好的折衷方法，它利用(x，y)点4 个最近邻像素的灰度值计算该点灰度值。设(x，y)点的四个最邻近像素为A、B、C、D，坐标分别为(i，j)、(i+1，j)、(i，j+1)、(i+1，j+1)，灰度值分别为g (A)、g (B)、g (C)、g (D)。首先设：

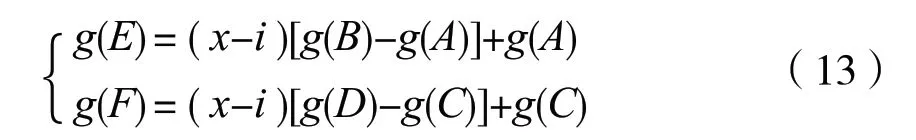
则(x，y)点的灰度值g (x′，y′)为

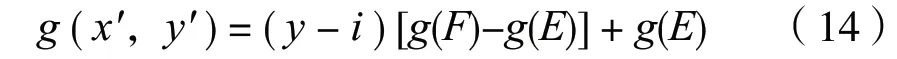
上述方法很容易推广到三维情况，设(x，y，z)点的8 个最邻近像素为O、P、Q、R、S、T、U、V，其坐标分别为(i，j，k)、(i+1，j，k)、(i，j+1，k)、(i，j，k+1)、(i+1，j+1，k)、(i，j+1，k+1)、(i+1，j，k+1)、(i+1，j+1，k+1)，灰度值分别为g (O)～ g (V)。计算四个点的灰度值有：

此时问题转化为二维情形，再通过式(13)和式(14)即可求出(x，y，z)点的灰度值。

5 结语

激光光斑的图像信息可以帮助人们直观地掌握激光能量密度分布，但由于受制于人眼对不同灰度级的识别能力，光斑灰度图像中所蕴含的丰富信息难以被充分利用。根据人眼对色彩非常敏感的视觉特性，通过正弦波函数调制的非线性伪彩色变换，将光斑的256 级灰度图像转换为色彩连续变化的伪彩色图像，而且随能量变化分布的色彩符合人们的视觉习惯，突出了光斑的特征。同时，经过空间灰度插值运算将离散的图像数据生成光斑的彩色三维模型，实现激光光斑能量分布结构的三维可视化，以反映光斑在不同区域能量分布的相对大小和位置，并可以通过3D 坐标变换进一步方便人们从各个角度观察激光的能量分布。

比较拟合前的准分子激光光斑的常规灰度图像（见图 2）和拟合后的光斑的二维伪彩色图像（见图3）以及激光光斑能量分布的三维重建能量密度示意图（见图 4）。不难发现经过灰度插值和伪彩色变换，光斑能量密度的三维模型过渡自然、色彩流畅，符合人的视觉习惯。针对拟合后的光斑图像进行三维伪彩色可视化处理，可以更直观地显示准分子激光光斑能量密度分布，定性和定量分析准分子激光光斑能量，从图像处理的角度为评价准分子激光治疗设备提供重要依据。

图2 拟合前的激光光斑灰度图像

图3 拟合后的激光光斑伪彩色图像

图4 激光光斑三维重建能量密度示意图

[1]单宝忠,王淑岩,牛憨笨,等.Zernike多项式拟合方法及应用[J].光学精密工程,2002,10(3)：88-93.

[2]杨枝灵,王开.数字图像获取、处理及实践应用[M].北京：人民邮电出版社,2003.

[3]张可村,赵英良.数值计算的算法与分析[M].北京：科学出版社,2003.

[4]章毓晋.图像处理和分析[M].北京：清华大学出版社,1999.

[5]刘钦圣.最小二乘问题计算方法[M].北京：北京工业大学出版社,1989.

[6]Hadenfeldt A C,Sayood K.Comp ression of Color2mapped Images [J].IEEE Transactions on Geoscience and Remote Sensing,1994,32(3) ：534-541.

[7]Lieberman DM,Grierson JW.A mathematical model for laser in situ keratomileusis and photorefractive keratectomy [J].J Refract Surg,2000,16：177-186.

[8]Mrochen M,Kaemmerer M,Mierdel P,et al.Principles of Tscherning aberrometry [J].J Refract Surg,2000,16(5)：570-571.

[9]HADENFELDT A C,SAYOOD K.Compression of color-mapped images[J].IEEE Transactions on Geoscience and Remote Sensing,1994,32(3)：534-541.

[10]Novak J,Miks A.Least-squares fitting of wavefront using rational function [J].Optics and Lasers in Engineering,2005,43(7)：776-787

[11]Bueeler M,Mrochen M.Maximum permissible lateral decentration in aberration sensing and wavefront-guided corneal ablation [J].J Cataract Refract Surg,2003,29：257-263.