优化三垂线定理教学之我见
郭雄英
摘要:在高中数学教学中,三垂线定理是非常重要的内容,要求学生必须重点掌握。三垂线定理及其逆定理是高考重点考核的知识点之一。因此,在教学中,教师如何将三垂线定理及其三垂线定理的逆定理讲透是非常重要的。本文针对于优化三垂线定理教学进行了具体的分析和研究。教师通过不断对三垂线定理进行优化教学,促进学生学习上的进步。
关键词:三垂线定理;逆定理;爪子定理;教学
0 前言
在高中数学教学中,针对于三垂线定理的教学,是重点的教学内容,教师需要采用有效的教学方法,提高学生学习三垂线定理及其三垂线定理的逆定理的学习效率,使学生能够全面的掌握三垂线定理及其三垂线逆定理的重点,并且将其融会贯通的应用到实际的解题当中。本文针对于三垂线定理主要进行如下几个方面的分析,对三垂线定理讲解的重点进行了研究,区分了三垂线定理以及逆定理,三垂线定理及其逆定理是爪子定理的特例这一事实,并且详细的探讨了如何灵活的的运用三垂线定理及其三垂线定理的逆定理。下面就进行具体的研究。
1 如何进行三垂线定理的讲解
在高中数学的教学中,教师只有想办法对三垂线定理进行有效的讲解,才能够使学生全面的掌握三垂线定理方面的相关知识。教师在进行三垂线定理讲解的时候,应该注意以下几个方面[1]。一是,在强化三垂线定理条件的时候,教师应该与学生一定对三垂线定理的内容进行解析,教师与学生一起对三垂线定理逐字逐句的进行解释,包括每个条件和结论的含义。二是,教师应该揭示三垂线定理及其逆定理的实质,三垂线定理及其逆定理是研究直线和直线之间垂直关系的。三是,应该拟清三垂线定理的结构关系。教师在进行三垂线定理教学的过程中,学生刚开始可能分不清各条直线之间的关系,教师应该帮助学生将所涉及的面与线,线与线之间的关系进行理顺,三垂线定理及其逆定理的条件和结论一共涉及到四线、三垂以及一平面[2]。因此,在实际学习中学生一定要先找出两个垂直,再推出第三个垂直。
2 正确区分三垂线定理及其逆定理
学生在实际的学习中,三垂线定理及其逆定理在理论上叙述非常的相似,很多学生在学生中,容易将三垂线定理和三垂线定理的逆定理混淆。因此,教师应该教授学生的鉴别的方法。实际上,三垂线定理是判定平面内一直线与该平面外的一直线(指斜线)垂直关系的,而三垂线定理的逆定理是判定平面内一直线与这平面的斜线在该平面内的射影的垂直关系的。三垂线定理及其三垂线定理的逆定理是有着本质的区别的。
3 三垂线定理及其逆定理是爪子定理的特例
在高中数学中,三垂线定理及其逆定理是爪子定理的一个特例所存在。
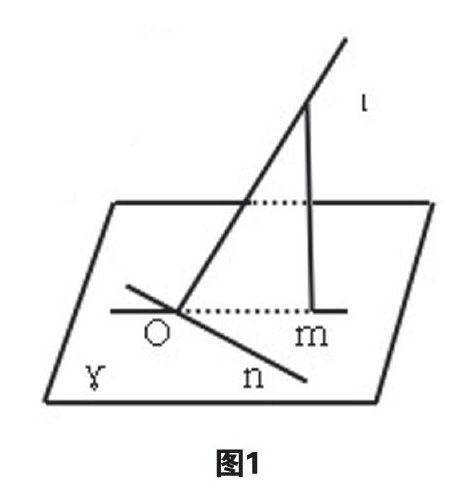
爪子定理是:如图1,ι是平面γ的斜线,m是ι在平面γ内的射影,n为γ内的任一直线,ι与平面γ所成的角为α,m与n所成的角为β,ι与n所成的角为θ,则cosθ=cosα·cosβ。
当β=90°时,必有θ=90°,此时为三垂线定理;
当θ=90°时,必有β=90°,此时为三垂线定理的逆定理。
4 如何灵活的的运用三垂线定理及其逆定理
在高中数学的教学中,教师对三垂线定理的教学,主要是为了学生能够灵活的运用三垂线定理,使学生能够运用三垂线定理解决实际的问题[7]。教师应该教会学生充分运用平面位置的变化打破定势思维习惯,通过下文的例题有意识的对学生加强训练,进而确保学生能够全面的掌握三垂线定理及其三垂线定理的逆定理。
例题:
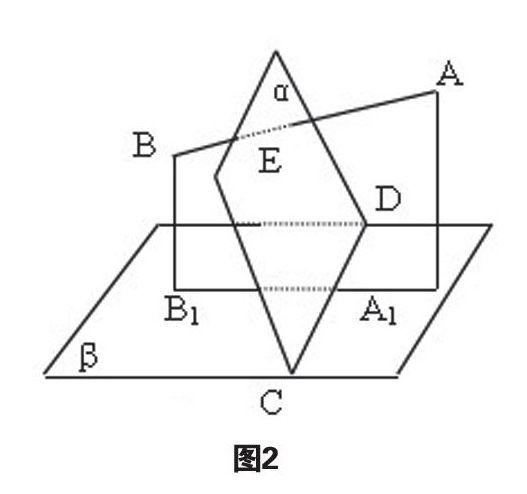
如图2所示,α∩β=CD,
AB⊥α于点E,AA1⊥β于点A1,
BB1⊥β于点B1,求证:CD⊥A1 B1
分析:
在本道习题中,一共涉及到2个平面,从图1上看,CD和A1 B1均在平面β上,因此,这属于内内二线,因此,我们在进行证明的时候针对于CD和A1 B1均在平面β上我们应该运用三垂线定理的逆定理进行论证。而由题目我们可以推出,AB⊥CD,因此,我们在进行证明的过程中,需要充分的利用这个条件,在本题中,我们可以将AB⊥CD理解为平面α的垂线一定会垂直于所处在平面α内的CD,由图1我们可以了解,平面α和平面β是相交的,因此,我们可以得知AB是β的斜线,而由题目中AA1⊥β于点A1,BB1⊥β于点B1,我们所得,A1 B1是斜线AB在平面β中的射影。又从,α∩β,我们可以得知AB⊥CD是平面β中直线CD垂直于平面β的斜线AB。通过依据题目和图1我们进行分析,进而理清了本题的证明思路,而本题主要就是应用三垂线定理的逆定理进行证明。
5 结束语
本文主要对优化三垂线定理的教学进行了具体的分析和研究,通过本文的探讨,我们了解到,教师在实际的教学中,需要采取相应的教学策略,使学生全面的掌握有关于三垂线定理及其逆定理的相关方面的知识。另外,在教学中,教师应该让学生充分的理解三垂线定理的实质和内涵,学生只有掌握三垂线定理的实质,才能够真正的掌握有关于三垂线定理的知识,在平时的数学学习中,解决实际的问题,进而不断的促进学生学习上的进步。
参考文献
[1] 张朝霞.浅谈三垂线定理的应用[J].赤峰教育学院学报。 2009(03)。
[2] 楼可飞. 三垂线定理及其逆定理的题根[J].高中数理化(高二版)。 2009(02)。
[3] 王志强.应用“垂面、三垂线定理”求“二面角”(高二)[J].数理天地(高中版)。 2011(03)。
[4] 胡燕丽,楼可飞.对三垂线定理及其逆定理的一点认识[J]. 数学大世界(高中辅导)。 2011(10)。
[5] 楼可飞.对三垂线定理及其逆定理的认识[J].数理天地(高中版)。 2011(06)。
[6] 王永怀,霍振化.“三垂线定理”的说课和点评[J].中学数学教学参考。 2011 (04)。
[7] 朱伟卫.例谈三垂线定理及其逆定理图形变换的训练[J].数学通报。 2009(06)。

