对反散射方法所得S-G方程解的数值模拟
史 伟,曹建莉
(河南工业大学 理学院,河南 郑州 450001)
对反散射方法所得S-G方程解的数值模拟
史 伟,曹建莉
(河南工业大学 理学院,河南 郑州 450001)
本文采用反散射方法得到给定初始值的条件下S-G方程的解,再利用maple软件编程选取适当的参数得到解的数值模拟.
S-G方程;反散射方法;maple软件
S-G方程是数学物理领域中的热点方程,反散射方法是孤立子理论中的一种经典方法,得到了广泛的应用[1-3],而与数学软件的结合却是近几年的事[4].本文讨论在给定初始条件q(x,t)|t=0=q(x),r(x,t)|t=0=r(x)时S-G方程的解,首先求出以初始条件中q(x),r(x)为位势的方程(1)的散射数据,然后求出当q(x,t),r(x,t)作为S-G方程解的时候,其相应的散射数据随时间的变化规律,最后由T-L-M积分方程组,根据散射数据来恢复q(x,t),r(x,t),最后用maple软件选取适当的参数给出S-G方程解的数值模拟.
1 S-G方程
首先考察一般特征值问题

其中q=q(x,t),r=r(x,t),并设φ1,φ2随时间t的演化规律为

其中A,B,C是x,t,ξ的函数,并设ξt=0,由φ1xt=φ1ix,及φ2xt=φ2tx推出A,B,C要满足以下三个方程

将A,B,C取为ξ的多项式

代入(3)并比较ξn+1的系数,得bn=cn=0;比较ξn的系数,可得anx=0,bnx+2ibn-1=-2qan,cnx-2icn-1=2ran.由此定出an=常数及bn-1,cn-1.如此反复,即可定出aj,bj,cj,比较ξ0的系数,给出非线性演化方程.取n=3,用maple软件计算得

(4),(5)中的系数a0,a1,a2,a3均为常数,适当选取这些常数,并取q(x),r(x)建立关系,方程可约化为:


2 利用反散射方法得到S-G方程的解定义

为S-G特征问题的散射数据.给定散射数据(8)后,再恢复S-G特征值问题(1)中的位势q(x),r(x).

积分方程(10)的解未必对所有的x都是存在唯一的.例如,当ρ(ξ)=(ξ)=0,上,下平面各有一个特征值λ(Imλ>0(Imλ<0)对应的归一化因子是c,,积分方程化为

用maple解代数方程得

设q(x),r(x)分别是方程(5),(6),(7)的解,q,r及其导数当|x|→∞时很快趋于零,当t=0时,q=q(x),r=r(x),而且以q (x),r(x)为位势的特征值问题(1)的散射数据为

因此,r=-q为实函数时的n孤子解为
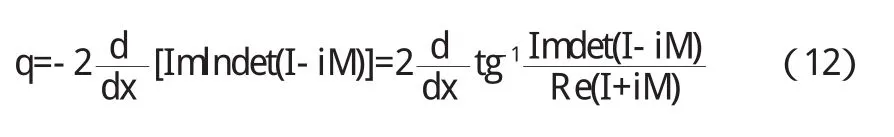
3 利用maple软件作图

用maple软件做图,并选择参数的值代入程序,运行程序得图1.

图1

图2

用maple软件做图,并选择参数的值代入程序,运行程序得图2.


用maple软件做图,并选择参数的值代入程序,运行程序得图3.

图3
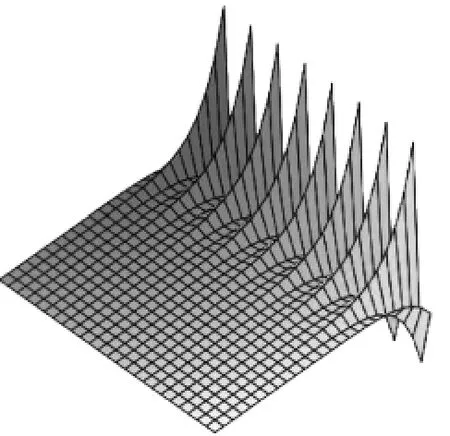
图4

用maple软件做图,并选择参数的值代入程序,运行程序得图(4).
4 总结
计算机科学的发展,使复杂、冗长的代数计算可以顺利完成,完成了人力所不能及的复杂计算,利用数学软件得到更多的精确解,还可以得到其解的数值模拟.
〔1〕李翊神.特征值问题,散射与反散射理论.南京大学学报,1987.
〔2〕LiYishen,Chin Ann moth.2(1981),147-156.
〔3〕L.Hormander,Complex Analysis in Several Variables, 1966.
〔4〕马开平.maple高级应用及经典实例.2002.
O241.82
A
:1673-260X(2013)01-0004-03
河南工业研究生创新基金资助(11YJCX 58);郑州市科技发展计划项目资助(20110306)

