输气管道泄漏音波信号传播特性及预测模型
孟令雅,付俊涛,李玉星,刘翠伟,刘光晓
(1.中国石油大学信息与控制工程学院,山东青岛 266580;2.中国石油大学储运与建筑工程学院,山东青岛 266580)
输气管道泄漏音波信号传播特性及预测模型
孟令雅1,付俊涛2,李玉星2,刘翠伟2,刘光晓2
(1.中国石油大学信息与控制工程学院,山东青岛 266580;2.中国石油大学储运与建筑工程学院,山东青岛 266580)
输气管道泄漏音波在管内传播过程中发生衰减,在安装音波传感器前必须明确管内音波信号的传播距离。综合考虑介质黏滞吸收和热传导作用及特殊管件(弯管、分支及变径管)的吸收作用,建立泄漏音波在管内传播模型。利用改进的小波分析法对泄漏音波信号时频域特征进行分析,模拟分析不同特殊管件对音波传播的影响,并利用高压泄漏试验装置对建立的传播模型进行验证。结果表明:泄漏音波在管内以平面波形式传播,泄漏信号幅值能量占优的频带主要集中在0~0.366 Hz及2.93~46.88 Hz内,直管和弯管对音波衰减影响较小,只有分支和变径(变径流量计、阀门)对音波传播影响较大;得到的拟合音波吸收系数与理论吸收系数吻合较好,模型计算结果较为准确,可提高音波泄漏检测的准确性。
输气管道;泄漏音波;传播模型;声学模拟;吸收系数
当输气管线发生泄漏时,由于管壁与管内介质的交互作用在管内产生压力波动,这一动态压力将通过管内介质以声速向管线上下游传递,从而形成泄漏音波[1-2]。通过在管线上下游安装音波传感器,检测这一动态压力,即可实现泄漏检测和定位[3]。 Muggleton等[4]针对充液圆管道中泄漏引起的声音和振动波的传播行为进行分析,推导出介质中充液管道的声振耦合系统的频散效应[5]。Kim等[6]利用时频联合分析的试验方法及边界元法得到了管道系统的声波的截止频率,Matjaz Prek[7]提出了利用频域分析确定弹塑性充液管内音波特性的方法,刘敬喜等[8]研究了弹性介质中充液管道的波衰减特性,利用沿实波数轴搜索求根的方法得到了频散方程的完全解。而气体由于可压缩性引起的音波信号传播特性明显不同于液体管线,并且必须考虑管内介质的黏滞吸收和热传导等作用和弯管、分支管或变径管等特殊构件引起的音波衰减[9]。笔者综合考虑黏滞吸收作用、热传导作用及特殊管件的吸收和反射作用,建立天然气长输管道泄漏音波的传播和衰减模型,得到泄漏音波在管内介质中的传播规律。
1 模 型
对于一般的声源在无界空间中辐射球面波,而将声源限制于受管壁束缚的管道中传播,当音波的频率低于圆管内平面波的截止频率时,管内音波会以一维平面波的模式进行传播。而圆管中平面波的截止频率[10]为

在管内能够长距离传播且可用作音波泄漏检测的音波频段主要集中在次声及可听声的低频部分(0~100 Hz),由式(1)可得,对于实际管线,当管径达到1219 mm时,频率小于163.4 Hz下音波在管内传播模式为一维平面波,因此对实际现场天然气管线,可以认为其传播模式为一维平面波形式。
1.1 介质黏滞吸收和热传导作用的影响
考虑黏滞吸收作用、热传导作用,对声波基本方程联立求解可得到音波信号阻尼波动方程[11-12]:
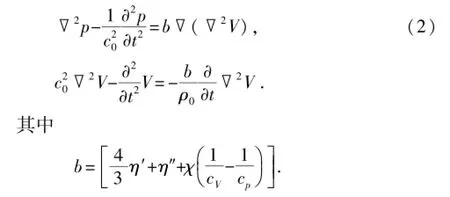
式中,η′、η″分别为切变黏滞系数和介质容变黏滞系数,Pa·s;χ为热传导系数,W/(m·K);cV为质量定容热容,kJ/(kg·K);cp为质量定压热容,kJ/(kg ·K)。
阻尼介质中声波声压传播方程为

式中,α为媒质的阻尼吸收系数,是描述声波振幅随距离衰减快慢的一个物理量;ρ0为介质密度,kg/m3; ω为角频率;f为声波频率,Hz,c为声波传播速度,m/ s;x为声波传播距离,m;k0为无阻尼波的波数。
式(3)代表着以传播速度为c,角频率为ω向正x方向传播的声波,其振幅为p0e-αx。
因此,音波沿管道传播的幅值衰减公式为

式中,r为管径,m;c0为传播速度,m/s。
1.2 不同特殊管件对泄漏音波传播的影响
当音波在管道中传播时,遇到一些特殊突变结构如弯管、变径、分支或障碍物时,声阻抗也会发生变化,使得音波信号发生不同程度的衰减。
根据试验管道模型分别对直管、弯管、分支和变径等结构对音波传播影响进行分析,利用ANSYS建立弯管等构件模型,网格模型采用六面体,并采用映射网络的方法进行划分(特殊结构采用四面体,自由划分),然后导入到声学软件SYSNOISE中进行声学处理,得到音波衰减规律。
通过计算管件入射和出口的声压来计算传递损失,在入口平面施加单位速度激励,出口施加全吸收边界条件,不考虑壁面的吸收作用。传递损失的计算公式[13]为

式中,pi、pt分别为管件入口声压和出口透射声压, Pa;S1、S2分别为管件入口截面和出口截面积,m2; u1为管线入口振速,m·s-1,ρ0、c0分别为管内介质的密度(kg/m3)和音速(m/s)。
图1为直管、弯管、分支和变径管模拟结果。直管段的管内径为10 mm,管长为10 m,压力为5 MPa;弯管段的管内径为10 mm,90°弯头,曲率半径为15 mm,压力为5 MPa;主干管段管内径为10 mm,管长为10 m,分支段长为20 cm,内径为8 mm,压力为5 MPa;变径管的入口、出口管内径10 mm,管长10 cm,变径管内径2 cm,管长20 cm,压力为5 MPa。
由图1可知:(1)不考虑介质黏滞性和热传导情况下,在管道本身的截止频率下,音波在直管道中的传播损失基本为0,高于管道截止频率,管内将出现高次模态波,而引起音波的损失;音波经过弯管时,音波的衰减较少,主要是管径较细,曲率半径较大的原因,考虑现场大管径弯管,会有较大的能量损失,但低频范围(0~100 Hz)内相对较少,不予考虑;(2)音波经分支管时,音波的衰减较小,但分支管长度等于音波波长的1/4的奇数倍时,管口产生强烈驻波共振而使音波的损失最大;音波经过流量计、阀门变径腔体或变径管时,将产生较大的衰减,衰减程度主要受变径前后管道尺寸影响,对试验室变径情况,不能忽略其影响,需要在建立实际音波传播模型时对其进行修正。

图1 不同特殊管件内音波传播规律Fig.1 Acoustic attentuation principle of different kinds of pipelines
因此在了解现场情况下,可以对理论传播公式添加修正经验系数,来修正理论模型的误差,即得到实际音波信号传播公式为

式中,σ为修正经验系数,通过对理论吸收系数和模拟结果的对比,可得,σ=1.2~3,现场需要根据实际情况确定。
此外分别对不同压力等级和不同管径下这些特殊管件的影响作用进行了模拟分析,其规律基本相似,基本不受压力的影响,只是随管径的增大,衰减作用逐渐突出。因此,结合试验室管线情况和模拟结果确定式(7)中的修正经验系数,在此取σ=2。
2 试 验
2.1 试验装置
利用高压输气管道泄漏检测装置[14],装置总长251.5 m,测试管段全长199.85 m,最高承压8 MPa,设计运行最高压力6.4 MPa,设计流量为60 m3/h,沿线共设有3个泄漏点,分别距起点音波传感器40.34、88.33和149.02 m,泄漏点由内置孔板的法兰和球阀构成,根据试验要求改变泄漏孔径,通过迅速开关阀门模拟泄漏发生。在3个泄漏点及管线起、终点处分别安装音波传感器,实时采集泄漏动态压力信号,从而保证在一个泄漏点模拟泄漏时,能够同时检测到泄漏点音波信号以及经过传播后的泄漏音波信号,从而研究不同泄漏位置、不同泄漏量等工况下音波信号的衰减情况。音波数据的采样率为3 kHz,试验装置流程如图2所示。

图2 高压输气管道音波泄漏检测装置Fig.2 Sonic leak detection test unit of high pressure gas pipeline
2.2 基于改进小波分析的泄漏特征时频分析
由于试验室采集到的泄漏音波信号为时域信号,由式(3)可得,研究泄漏音波信号的传播特性,需要获取音波信号的频域特性,尤其是泄漏时刻能量占优的频段,但单纯的频谱分析不适于泄漏音波信号这种突变信号,因此需要对泄漏音波信号进行时-频联合分析。采用改进的小波分析法(单子带改进的分解和重构算法)[15]对采集的泄漏音波信号进行时频分析,从而获得泄漏时刻某一微小频带内泄漏音波能量占优的频带及频带对应的幅值。
选取小波基为sym5小波,小波尺度选为12,子带序号为A12、D12、D11、D10、D9、D8、D6、D5、D4、D3、D2、D1时,频率分别为0~0.366、0.366~0.732、0.732~1.465、1.465~2.93、2.93~5.86、5.86~11.72、23.44~46.88、46.88~93.75、93.75~187.5、187.5~375、375~750、750~1500 Hz。对1~5 MPa下泄漏点1发生0.6 mm孔径的泄漏进行时频分析,得到不同频带内幅值分布规律如图3所示。
通过图3可得,1~5 MPa下幅值能量占优的频带主要集中在0~0.366及2.93~46.88 Hz内,基本不随压力的变化而变化,因此对泄漏音波信号的传播特性的研究主要集中在以上能量占优的频带内。

图3 1~5 MPa下幅值随频率分布Fig.3 Amplitude distribution with frequency from 1 to 5 MPa
2.3 模型验证
利用式(5)和(7),以5 MPa下泄漏点1发生0.6 mm孔径泄漏时A12、D6、D7和D9频带内幅值衰减为例进行拟合,其结果如图4所示。由图4可得,试验室测得的主要能量占优的频带幅值衰减规律与拟合的指数衰减规律相吻合。进一步拟合得到了不同压力、不同频带下音波吸收系数,如图5所示。

图4 不同频带下音波幅值随距离变化的拟合曲线Fig.4 Fitted curves of acoustic amplitude with distance changing in different subbands
由图5可得,由式(5)和(7)得到的理论吸收系数与由试验数据拟合的拟合吸收系数基本吻合,且在较低频率下吻合较好,随着频率的增大,由于频带包含的频率成分增多,而理论计算得到的是频带中心频率(频带取平均值)处的吸收系数,因此随频带频率的增大出现一定的误差,但影响不大。因此,本文建立起的音波在管中的传播理论模型能较好地反映音波在管内的传播规律,实际在计算音波传感器的安装距离时,可以采用该模型进行计算。
根据建立的实际音波传播和衰减模型,分别研究不同压力等级1~5 MPa、不同管径(273~1 016 mm、不同频率音波信号(0~50 Hz)在管内的传播和衰减情况。在此取修正经验系数σ=1.5,温度取20℃,管内介质为天然气,天然气的相对密度取0.6,气体绝热指数取1.33,压缩因子取0.918,结果如图6所示。由图6可得,随着压力、管径的增大,音波信号衰减相同的幅度后,所能传播的有效距离逐渐增大,即在高压力、大管径下更容易检测到泄漏;随着频率的增大,音波信号的传播距离逐渐减小,且在该工况下,0.2 Hz音波信号幅值衰减为原信号0.7倍,所能传播的最大距离为100 km,因此利用音波信号中的低频部分检测泄漏具有较大的优势。

图5 不同压力下不同频带内音波吸收系数变化规律Fig.5 Absorption coefficient changing principle under different pressure in different subbands
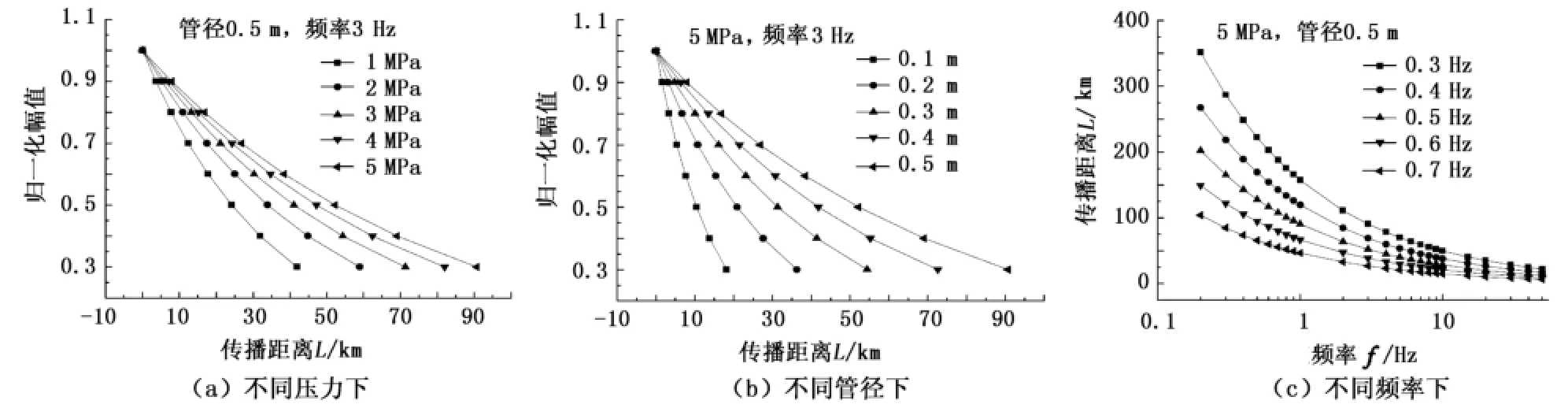
图6 不同工况下音波信号衰减规律Fig.6 Attenuation principle of acoustic signal under different conditions
3 结 论
(1)泄漏音波在管内传播的模式为一维平面波形式,其传播过程受到介质黏滞吸收和热传导作用以及特殊管件(弯管、分支、变径)的吸收作用的影响。
(2)泄漏信号幅值能量占优的频带主要集中在0~0.366及2.93~46.88 Hz内。
(3)在泄漏音波的研究频段,直管和弯管对声波衰减影响较小,只有分支和变径(变径流量计、阀门)对音波传播影响较大,当以上两种管件存在时需要对传播模型进行修正。
(4)泄漏音波信号在管内的传播遵循指数衰减的规律,且理论吸收系数和拟合值吻合较好,证明了本文理论模型的正确性。
[1] 孟令雅,李玉星,宋立群,等.输气管道泄漏音波传播特性及检测定位[J].天然气工业,2010,30(11):1-6. MENG Ling-ya,LI Yu-xing,SONG Li-qun,et al.A-coustic propagation characteristics,position monitoring and locating of gas transmission pipeline leakage[J].Natural Gas Industry,2010,30(11):1-6.
[2] MENG Ling-ya,LI Yu-xing,WANG Wu-chang,et al. Experimental study on leak detection and location for gas pipeline based on acoustic method[J].Journal of Loss Prevention in the Process Industries,2012,25(1):90-102.
[3] 付俊涛,李玉星,孟令雅,等.输气管道泄漏音波与干扰信号特征提取[J].石油化工高等学校学报, 2012,25(2):1-8.
FU Jun-tao,LI Yu-xing,MENG Ling-ya,et al.Characteristic extraction of acoustic leak signals and interfering signals for natural gas pipeline[J].Journal of Petrochemical Universities,2012,25(2):1-8.
[4] MUGGLETON J M,BRENNAN M J,PINNINGTON R J. Wave number prediction of waves in buried pipes for water leak detection[J].Journal of Sound and Vibration, 2002,249(5):939-954.
[5] MUGGLETON J M,BRENNANA M J,LINFORD P W. Axisymmetric wave propagation in fluid-fllled pipes:wave number measurements in invacuo and buried pipes[J]. Journal of Sound and Vibration,2004,270:171-190.
[6] KIM Min-Soo,LEE Sang-Kwon.Detection of leak acoustic signal in buried gas pipe based on the time—frequency analysis[J].Journal of Loss Prevention in the Process Industries,2009,22:990-994.
[7] MATJAZ Prek.Analysis of wave propagation in fluidfilled viscoelastic pipes[J].Mechanical Systems and Signal Processing,2007,21:1907-1916.
[8] 刘敬喜,李天匀,刘土光,等.弹性介质中充液管道的波衰减特性[J].华中科技大学学报:自然科学版, 2003,31(10):90-92.
LIU Jing-xi,LI Tian-yun,LIU Tu-guang,et al.The attenuation characteristics of waves in fluid-filled pipes surrounded by elastic media[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2003,31(10):90-92.
[9] 何琳,朱海潮,邱小军.声学理论与工程应用[M].北京:科学出版社,2006.
[10] 马大猷.现代声学理论基础[M].北京:科学出版社,2004.
[11] 王保国,刘淑艳,黄伟光.气体动力学[M].北京:北京理工大学出版社,2005.
[12] 李玉星,姚光镇.输气管道设计与管理[M].东营:中国石油大学出版社,2009.
[13] 康钟绪.消声器及穿孔元件声学特性研究[D].哈尔滨:哈尔滨工程大学,2009.
KANG Zhong-xu.Study on the acoustic characteristics of silencers and perforated elements[D].Harbin:Harbin Engineering Unversity,2009.
[14] 李玉星,唐建峰,王武昌,等.输气管道声波泄漏监测试验装置的设计与构建[J].试验技术与管理, 2010,27(8):63-67.
LI Yu-xing,TANG Jian-feng,WANG Wu-chang,et al. Design and construction of an experimental device for acoustic leak detection in gas pipelines[J].Experimental Technology and Management,2010,27(8):63-67.
[15] 许珉,程兴民.基于单子带重构改进小波变换的电力系统谐波检测方法[J].电力自动化设备,2008, 28(9):10-14.
XU Min,CHENG Xing-min.Harmonic detection based on wavelet transform improved by single-band reconstruction[J].Electric Power Automation Equipment, 2008,28(9):10-14.
(编辑 沈玉英)
Propagating characteristics of acoustic leakage signal in natural gas pipeline and establishment of prediction model
MENG Ling-ya1,FU Jun-tao2,LI Yu-xing2,LIU Cui-wei2,LIU Guang-xiao2
(1.College of Information and Control Engineering in China University of Petroleum,Qingdao 266580,China;
2.College of Pipeline and Civil Engineering in China University of Petroleum,Qingdao 266580,China)
The acoustic signals collected from natural gas pipeline leak detection inevitably attenuate as they propagate in the pipeline,and the propagation distance of acoustic signals must be calculated before installing acoustic sensors.With regard to the viscous absorption,heat conduction of medium and the absorption of the special pipe fittings(elbows,branch and adjustable tube),the propagation model of acoustic signals was established.The characteristics of acoustic leakage signals in timefrequency domain were analyzed by the improved waveform analysis method.The effects of different special fittings on sound wave propagation were simulated,and the acoustic propagation model was verified by a high pressure leakage test device. The results show that the acoustic leakage signals in the gas pipeline propagates in the form of plane wave,and the energy of acoustic leakage signals is concentrated in the 0-0.366 Hz and 2.93-46.88 Hz.The straight pipe and elbows have little effect on the propagation of acoustic signals,while branches and adjustable tube have great impact on the propagation.The acoustic absorption coefficient fitted by experimental data agrees well with that calculated by the propagation model,which proves the accuracy of the propagation model.The accuracy of the acoustic leakage detection is improved.
natural gas pipeline;acoustic leakage signal;propagation model;acoustic simulation;absorption coefficient
TE 973.6
A
1673-5005(2013)02-0124-06
10.3969/j.issn.1673-5005.2013.02.021
2012-09-28
国家自然科学基金项目( 51104175;51074175);中央高校基本科研业务费专项(11CX06075A)
孟令雅(1973-),女,副教授,博士,研究方向为天然气管道输送泄漏检测。E-mail:chuyunlcw@163.com。

