紧急控制下最优切机控制的控制变量权值取值
赵振元,陈维荣,张雪霞
(西南交通大学电气工程学院,成都 610031)
紧急控制下最优切机控制的控制变量权值取值
赵振元,陈维荣,张雪霞
(西南交通大学电气工程学院,成都 610031)
切除发电机会减小系统的惯性时间常数,进而影响系统的暂态稳定水平。根据惯性时间常数变化对系统暂态稳定水平产生的影响和线性规划理论,提出了一种电力系统暂态稳定紧急控制下最优切机控制的控制变量权值的取值方法。合理地调整切机控制量权值的大小,使经加权后计算得到的控制策略能够提高系统的暂态稳定水平,从而改进控制策略和控制效果,且物理意义明确。通过新英格兰39节点算例验证了所提出的切机控制变量权值取值方法的有效性。
暂态稳定;紧急控制;最优控制;切机控制量权值;惯性时间常数
暂态稳定计算方法分为直接法和时域仿真法。基于直接法或扩展等面积法,文献[1]使用暂态能量裕度的灵敏度来计算切机量;文献[2]针对紧急控制优化决策中存在的问题,提出了一种候选控制措施筛选法。由于直接法不考虑实际受扰轨迹,且假设较多,当考虑复杂模型时,直接法的复杂性将大大增加,同时计算精度也难以保证,存在计算结果鲁棒性和精确性差的缺陷[3]。
在时域仿真法中,文献[4]将紧急控制决策描述为最优控制问题;文献[5]根据暂态稳定约束函数对各控制点的灵敏度进行优化计算,有效防止了过切问题;文献[6]建立了暂态稳定紧急控制非线性规划模型,并给出近似规划算法和贪婪法算法两种求解方法,但模型中控制变量权值为缺省值,即所有权值均设为1;文献[7]基于时域仿真给出暂态稳定预防控制的非线性规划模型,该模型与时域仿真具有同等的模型适应性,其中控制变量权值取为发电机有功输出调整的单位调整代价,但均取为相同数值,故权值在优化模型中并未发挥作用,物理意义不明确;文献[8,9]均对暂态稳定紧急控制算法进行了改进,前者将理论算法与实际电网安全稳定控制系统的配置情况和运行要求相结合,后者对稳定判据、积分步长和微步系数做出进一步的改进,但均未给出控制变量权值的取值方法。
本文针对电力系统紧急控制措施,只考虑切机控制,并根据电力系统在施加切机控制后,各受控机组惯性时间常数的变化对系统暂态稳定水平产生的影响,对各个控制量的权值进行取值,从而调整控制策略,使得施加控制后各机组惯性时间常数的变化能对系统暂态稳定水平产生有利的影响,从而改进控制策略和控制效果,物理意义清晰明确。
1 最优切机控制数学模型
电力系统施加紧急切机控制前后的暂态过程微分代数方程组描述为

式中:x为各发电机组的状态变量向量;x0表示系统状态变量的初值;y为系统的代数变量向量;u为控制向量,其分量ui(i=1,2,…,r)为第i个切机点实际切除功率量与可切除总功率量之比,r是可切发电机节点数目。设紧急控制动作时间为tcl,则对于控制向量u,当t<tcl时,u=0;当t=tcl时,u发生突变;在t>tcl后,u保持为常数。
紧急控制的目的是为了保持系统的暂态稳定性,而暂态稳定性通常由发电机转子间最大相对摇摆角δmax来判断,考虑到应尽量减少控制结果的保守性,则可以适当地选定某一终端时刻tend,使该时刻下的δmax不大于规定值,tend的选取与所考虑的稳定性要求有关,本文考虑首摆失稳模式,将tend取为1.8 s。
切机控制算法应在保持电力系统稳定的前提下尽量少切发电机,控制算法模型的目标函数为

式中,Pi为可控发电机节点的总有功功率。
若考虑到各控制变量的权重,将式(2)转换成以切机代价最小为目标,以电力系统暂态稳定为约束条件的最优切机问题的数学模型,即
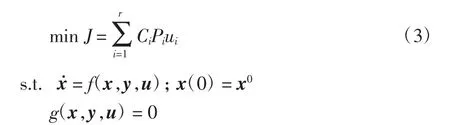
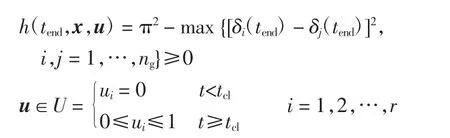
式中:Ci为可控发电机节点所对应的权值;δi(tend)为第i节点发电机在控制量为u的情况下tend时刻的功角;ng为发电机节点个数。
2 模型转换
传统的最优控制算法在解决复杂的电力系统最优控制问题时显得较为困难。在最优切机问题中,切机控制变量本身就是常量,无需参数化,故可方便地利用控制参数化算法,通过求出约束函数对控制变量的梯度,将问题转化为一般数学规划问题[10,11]。对于式(1)描述的系统,其梯度的具体计算公式[9]为
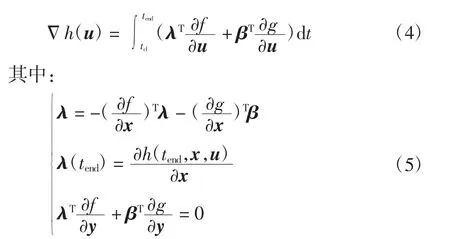
求出稳定约束函数对控制变量的梯度后,将暂态稳定紧急控制下最优切机控制模型转化成一组线性规划问题,转化后的线性规划问题描述[9]为
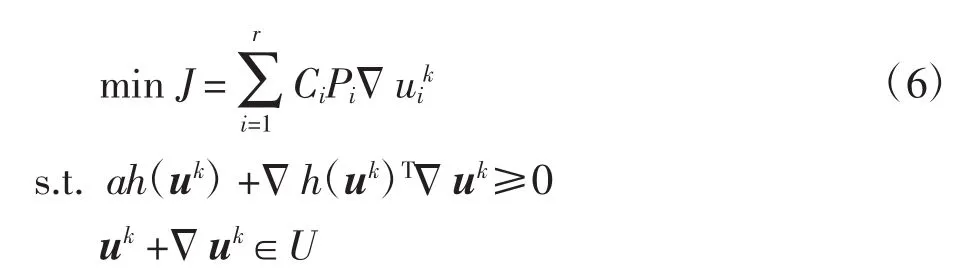
式中:k为迭代次数,将计算结果代入系统,重新进行时域仿真,若系统仍不稳定,再计算,如此迭代,直至系统稳定为止;a为微步系数,a的取值[9]与故障的严重程度有关,一个合适微步系数可以减少算法的计算量。
3 控制量权值的取值
实际稳定控制操作中,在切机地点的选择上,往往是优先切除水电机组。如果需要切除火电机组,则按照均衡分散的原则进行切除,即首先切除每个可切火电厂的1台发电机组,若不够再切第2台[12],以此类推。相应地调整各个控制量的权值,可满足上述切机顺序原则。切机控制量的权值也可取为发电机组功率输出调整的单位调整代价[7],k$/(MW·h),将暂态紧急控制问题转变为以切机控制经济代价最小为目标的最优控制问题。
上述两种控制量权值的取值方法,分别从电力系统实际操作出发以及从考虑切机控制的经济性出发。然而,当电力系统失稳后,切机控制的效果与切机地点、切除量大小等因素均有关,上述对控制量权值取值的方法只考虑了系统实际运行的一些要求,均是外在因素,而不是根据内在因素,即系统本身的暂态稳定水平要求来取值。所以,这种方法的物理意义不明确。
由于切除发电机的同时也会带走一定量的惯性时间常数,所以,在实施切机控制后,系统惯性时间常数将发生变化,进而会影响电力系统暂态稳定水平。送端与受端发电机组的惯性时间常数的变化对系统暂态稳定水平的影响与送受两端系统出力大小有关[13]。切机控制会减小系统惯性时间常数,故只考虑不同侧机组惯性时间常数减小对系统暂态稳定水平的影响。若将系统中各机组分为2类,第1类机组的惯性时间常数减小能提高系统暂态稳定水平,而第2类机组的惯性时间常数减小会致使系统暂态稳定水平降低,因此,在暂态稳定切机控制中,应尽量或优先切除第1类机组,而避免切除第2类机组。相应地,第1类机组所对应的切机控制量权值的大小应小于第2类机组对应的控制量权值。
根据机组惯性时间常数的变化对系统暂态稳定水平的影响,对切机控制量进行加权,其目的是为了在计算过程中起到引导或趋向的作用,控制变量应该满足经控制后的电力系统能保持暂态稳定的要求,起到改变切机顺序及优先或避免切除某些机组的作用,因此,两类受控机组的控制变量权值大小应合理。若两类机组的切机控制变量权值大小相差过大,则可能会出现过切或不收敛的情况,计算得到的控制措施不能保持电力系统暂态稳定;若二者大小相差过小,控制量权值可能在计算过程中起不到作用,相应的计算结果与权值为缺省值时的情况一样。为满足上述要求,通过计算试验,将第1类机组的切机控制量权值取为1,第2类机组的控制量权值取为1.4。
基于电力系统暂态稳定紧急控制的最优切机算法的主要步骤如下。
步骤1对控制量权值Ci进行取值;
步骤2置迭代次数k=0,设定初值u0=0;
步骤3进行系统时域仿真,计算约束函数h(uk);
步骤4若k=0,h(uk)≥0,说明系统无需控制即可保持暂态稳定,计算结束;否则转下一步。
若k≠0,h(uk)≥0,则计算若|Lk+1-Lk|<ε,ε为给定的精度要求,则计算结束;若h(uk)≥0,但|Lk+1-Lk|≥ε,则置h(uk)为其相反数;否则转下一步;
步骤5调整微步系数a;
步骤6计算各控制变量的梯度,求解式(6)所描述的线性规划问题,得到uk+1=uk+Δuk,并按实际情况离散化uk+1;
步骤7置k=k+1,返回步骤2。
4 算例计算
4.1 算例
算例采用新英格兰10机39节点系统,如图1所示,网络中选取节点30~38所连接的9台发电机(G1~G9)作为切机控制点,每个受控节点的等级数均为10级,即将这些发电机平均分为10级。本文利用电力系统分析工具箱PSAT2.1.6(power system analysis toolbox)对算例系统进行时域仿真,所有发电机均采用4阶带励磁的模型,并设G2为平衡机,精度要求ε=0.1MW。借助仿真软件,可方便地由摄动法或差分法求出各个切机控制量的梯度,本文采用差分法计算梯度。
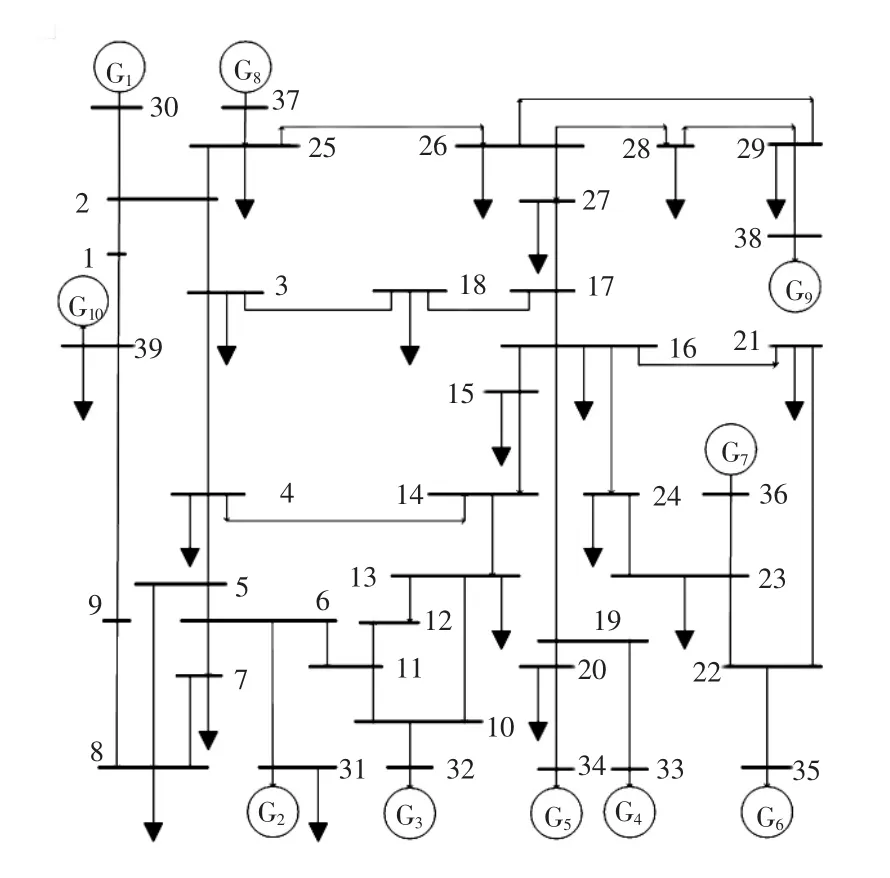
图1 新英格兰39节点系统接线示意Fig.1 Sketchmap of New England 39-buspower system
4.2 算例计算过程
节点16在0 s时发生三相接地短路故障,0.12 s时故障清除,0.2 s时进行切机。未采取任何控制措施,系统失去暂态功角稳定,如图2所示。
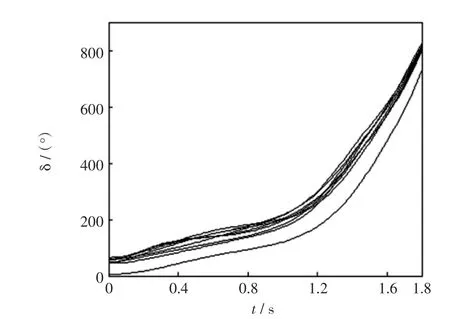
图2 未施加控制的各相对转子角摇摆曲线Fig.2 Relative rotor angle sw ing curvew ithout control
首先不对切机控制变量进行加权,利用最优切机控制算法进行计算。当不采取任何稳定控制措施时,tend时刻系统的最大相角差为816.46°,计算出其对应的稳定约束值为-193.18。在故障发生后0.2 s进行切机,计算切机点的梯度,计算结果见表1。
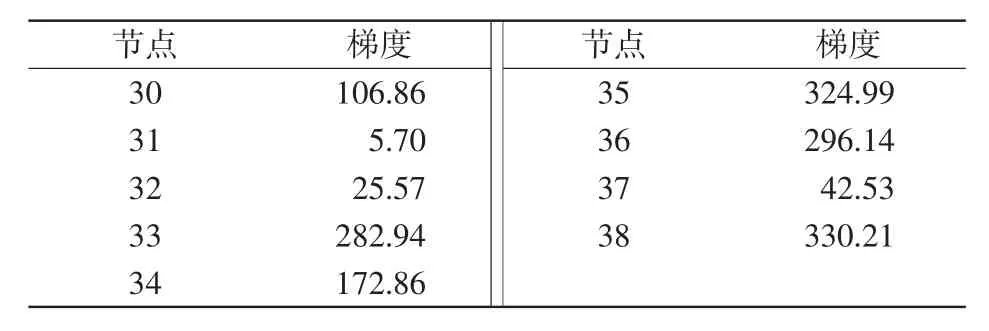
表1 不采取控制措施时的切机点梯度Tab.1 Gradientofgenerator-sheddingw ithout control
第1次迭代结果为在36节点切除2台发电机。第1次施加控制后系统tend时刻最大相角差为676.66°,对应的稳定约束值为-129.61,系统未保持暂态稳定,计算各切机点的梯度,见表2。
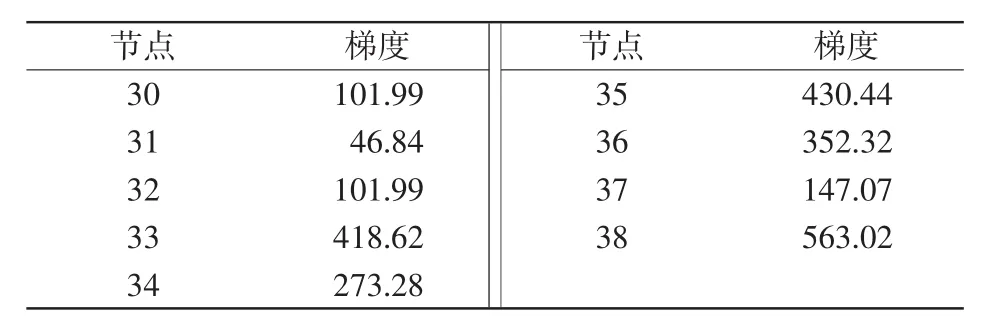
表2 采取第1次控制措施后的切机点梯度Tab.2 Gradientof generater-shedding under the first control
第2次迭代结果为在36节点切除2台发电机,在38节点切除1台发电机,第2次施加控制后系统tend时刻最大相角差为522.54°,对应的稳定约束值为-73.30,系统未保持暂态稳定,继续计算对各切机点的梯度,见表3。
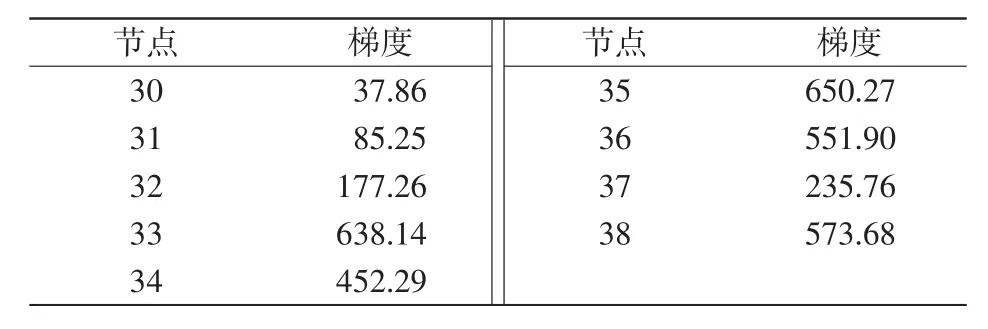
表3 采取第2次控制措施后的切机点梯度Tab.3 Gradientof generater-shedding under the second control
第3次迭代结果为在33节点切除1台发电机,在36节点切除2台发电机,在38节点切除1台发电机。第3次施加控制后系统tend时刻最大相角差为252.10°,对应的稳定约束值为-9.49,系统未保持暂态稳定,各切机点的梯度见表4。
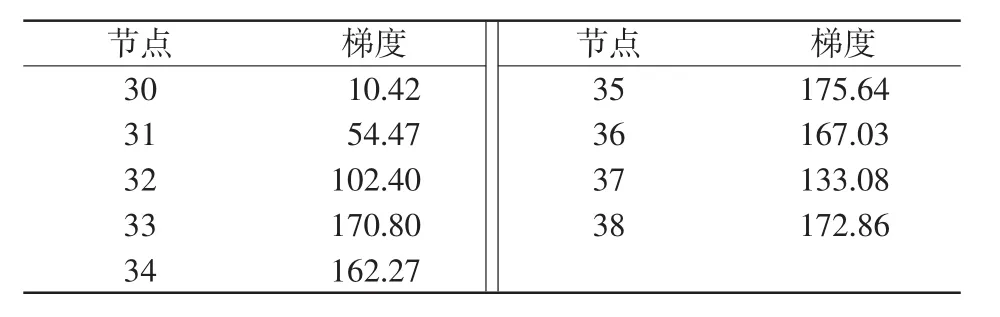
表4 采取第3次控制措施后的切机点梯度Tab.4 Gradientof generater-shedding under the third control
第4次迭代结果为在33节点切除1台发电机,在34节点切除1台发电机,在36节点切除2台发电机,在38节点切除1台发电机。经上述控制后,系统tend时刻系统的最大相角差为124.31°,小于180°,根据系统最大相对角摇摆曲线可看出系统可以保持暂态稳定,且满足计算精度要求,停止计算。施加控制后的系统暂态功角摇摆曲线如图3所示。
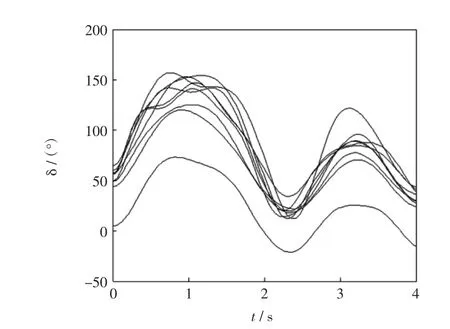
图3 不加权切机控制后各相对转子角摇摆曲线Fig.3 Relative rotor angle sw ing curvesafter generator-shedding controlw ithoutweighted
对切机控制变量进行加权,节点16发生故障,相对于这一故障断面,G4~G7处于送端,G1、G2、G3、G8和G9处于受端,送端系统出力为2 350MW,受端系统出力为3 835MW,送端系统出力小于受端系统出力,且相差较大。此时送端系统惯性时间常数减小会提高系统暂态稳定水平,受端系统惯量减小会降低系统暂态稳定水平[13],应尽量切除送端系统的机组,故取C33~C36为1,C30、C31、C32、C37和C38为1.4。
对控制变量进行加权后,第1次迭代的计算结果与控制变量未加权时的相同,第2次迭代的计算结果变为在节点33切除1台发电机,在节点36切除2台发电机。施加控制后系统tend时刻最大相角差为566.08°,对应的稳定约束值为-87.74,系统未保持暂态稳定,计算对系统施加第2次控制后各切机点的梯度,见表5。
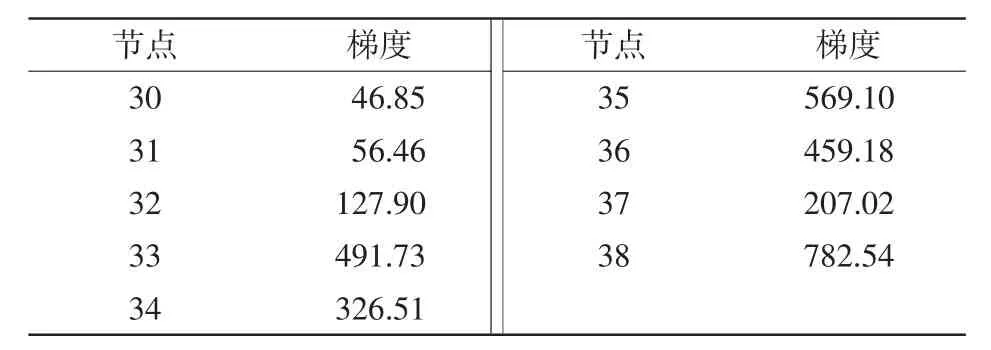
表5 采取第2次控制措施后的切机点梯度(加权后)Tab.5 Gradientgenerater-shedding under the second controlw ith weighted
第3次迭代的计算结果为在节点33和节点35分别切除1台发电机,在节点36切除2台发电机。施加控制后系统tend时刻最大相角差为365.55°,对应的稳定约束值为-30.83,系统未保持暂态稳定,计算对系统施加第3次控制后的各切机点的梯度,见表6。
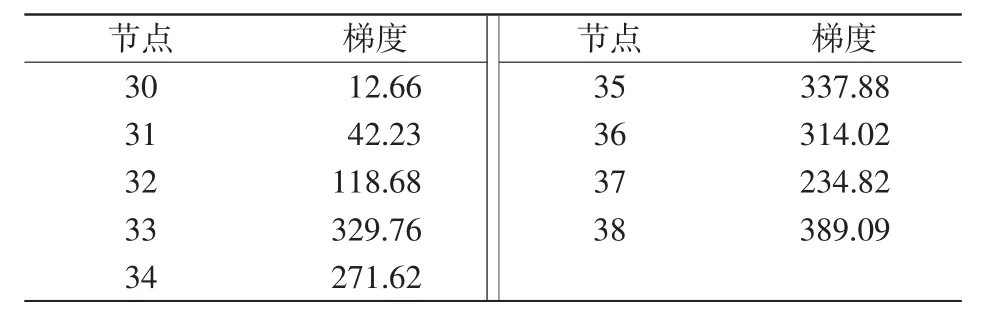
表6 采取第3次控制措施后的切机点梯度(加权后)Tab.6 Gradientgenerater-shedding under the third controlw ith weighted
第4次迭代计算所得结果为在33节点和35节点分别切除1台发电机,在36节点切除3台发电机。经上述控制后,系统可以保持暂态稳定,且满足计算精度要求,停止计算。施加控制后的系统暂态功角摇摆曲线见图4。
根据线性规划理论[14],两类机组的控制变量权值取值相差要适中。若相差太小,权值在计算中将起不到作用,计算所得到的结果与未加权时的计算结果一样;若相差过大,虽然在计算过程中,权值可以明显起到作用,但也可能会造成过切(如在一个切机点切除台数过多),或系统的最大相角差越来越大,计算结果不收敛。
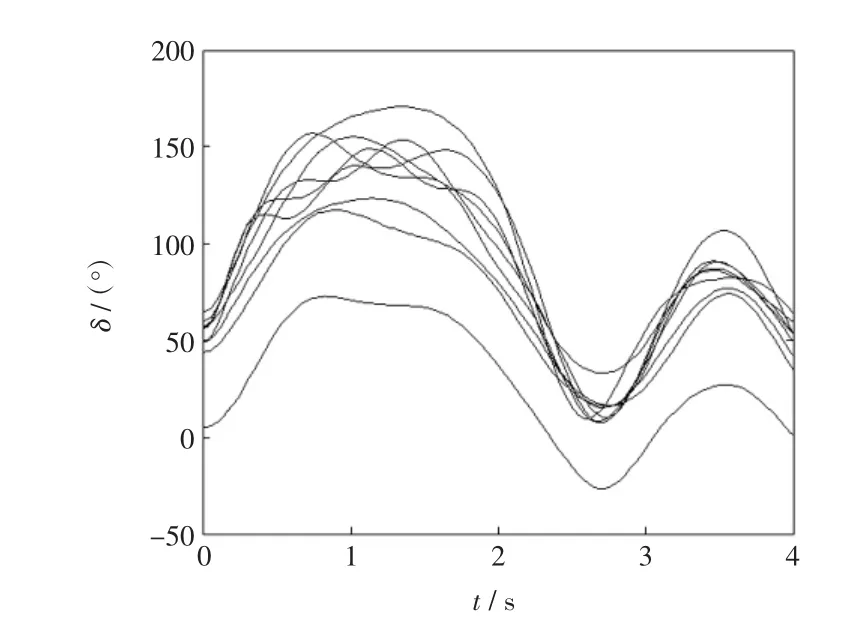
图4 加权切机控制后各相对转子角摇摆曲线Fig.4 Relative rotor angle sw ing curvesafter generator-shedding controlw ith weighted
4.3 算例结果分析
以上2个算例不加权和加权后的最优切机控制结果见表7,施加控制后的系统暂态最大功角摇摆曲线如图5所示。

表7 不加权和加权的最优切机控制结果对比Tab.7 Results com parison of theoptimal generator-sheddingmethodsbetween weighted and unweighted
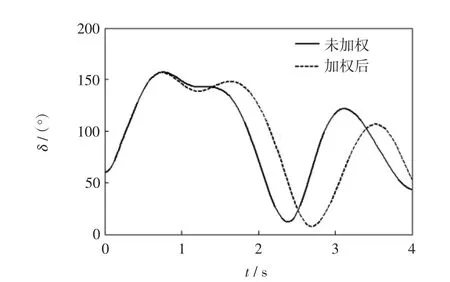
图5 切机控制后最大相对转子角摇摆曲线Fig.5 Biggest relative rotor angle swing curves under generator-shedding control
根据表7和图5,相比较未加权时的控制措施,加权后的最优切机控制措施尽量切除送端发电机,相应的切机总量和系统暂态功角摇摆曲线的最大幅值和幅度都有所减小,振荡周期变长,系统暂态稳定水平提高。
5 结论
(1)根据机组惯性时间常数的变化对系统暂态稳定水平的影响,对暂态稳定最优切机控制的控制变量进行加权,可以避免或尽量切除某些机组,物理意义清晰明确,所求得的控制策略可以提高系统的暂态稳定水平。
(2)如此加权也可以改进控制策略,起到减少总切机量的作用。
(3)针对系统中的不同故障,根据其所处具体断面的位置和断面上潮流的走向,可以将系统中各发电机组划分为受端机组和送端机组,再根据两端机组的出力情况,对切机控制变量进行加权。因此,本文所提出的加权方法对于电力系统中严格的断面故障控制策略及控制效果的改进更为有效。
[1]滕林,刘万顺,貟志皓,等(Teng Lin,Liu Wanshun,Yun Zhihao,etal).电力系统暂态稳定实时紧急控制的研究(Study of real-time power system transientstability emergency control)[J].中国电机工程学报(Proceedingsof the CSEE),2003,23(1):64-69.
[2]余贻鑫,杨涛,刘辉(Yu Yixin,Yang Tao,Liu Hui).一种暂态稳定紧急控制策略筛选法(Filteringmethod for transient stability emergency control strategy)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(5):1-4,88.
[3]甘德强,辛焕海,王建全,等(Gan Deqiang,Xin Huanhai,Wang Jianquan,etal).暂态稳定预防控制和优化新进展(Progress in transientstability preventive controland optimization)[J].电力系统自动化(Automation ofElectric Power Systems),2004,28(10):1-7.
[4]王建全,王伟胜,朱振青,等(Wang Jianquan,Wang Weisheng,Zhu Zhenqing,etal).电力系统最优切负荷算法(Optimal load-shedding algorithm in power system)[J].电力系统自动化(Automation of Electric Power Systems),1997,21(3):33-35,38.
[5]毕兆东,王建全,韩祯祥(Bi Zhaodong,Wang Jianquan,Han Zhenxiang).基于数值积分法灵敏度的快速切负荷算法(A fast load shedding algorithm based on integration sensitivity)[J].电网技术(Power System Technology),2002,26(8):4-7,43.
[6]常乃超,陈得治,于文斌,等(Chang Naichao,Chen Dezhi,YuWenbin,etal).基于受控微分-代数系统灵敏度分析的紧急控制(Emergency controlbased on sensitivity analysisof controlled differential-algebraic systems)[J].电力系统自动化(Automation of Electric Power Systems),2003,27(17):19-22,91.
[7]房大中,孙景强(Fang Dazhong,Sun Jingqiang).基于最优控制原理的暂态稳定预防控制模型(Transientstability preventive controlmodel based on optimal control in power system)[J].电力系统自动化(Automation of Electric Power Systems),2005,29(1):18-21.
[8]任伟,房大中,陈家荣,等(RenWei,Fang Dazhong,Chen Jiarong,etal).基于最优控制原理的电力系统紧急控制及应用(Optimal control theory based power system emergency control and its application)[J].电网技术(Power System Technology),2009,33(2):8-13.
[9]王彪,方万良,罗熙之(Wang Biao,FangWanliang,Luo Xizhi).紧急控制下最优切机切负荷方案的快速算法(A fast algorithm of optimal generator and load-shedding foremergency control)[J].电网技术(Power System Technology),2011,35(6):82-87.
[10]Ota H,Kitayama Y,Ito H,et al.Development of transient stability control system(TSC System)based on on-line stability calculation[J].IEEE Trans on Power Systems,1996,11(3):1463-1472.
[11]Teo K L,Goh C J,Wong K H.A Unified Computational Approach to OptimalControl Problem[M].England:Longman Scientific and Technical,1991.
[12]任伟(RenWei).基于暂态能量的电力系统暂态稳定切机控制研究(Study on Generator Tripping Control Based on Transient Energy for Transient Stability in Power System)[D].天津:天津大学电气与自动化工程学院(Tianjin:School of Electrical Engineering and Automation,Tianjin University),2009.
[13]赵振元,陈维荣,戴朝华,等(Zhao Zhenyuan,Chen Weirong,DaiChaohua,etal).系统惯性时间常数对互联电网暂态稳定水平的影响(Influence of system inertia time constantson transientstability levelof interconnected AC power grid)[J].电网技术(Power System Technology),2012,36(1):102-107.
[14]束金龙.线性规划理论与模型应用[M].北京:科学出版社,2003.
Valueof ControlVariableW eightof OptimalGenerator-shedding Control for Emergency Control
ZHAOZhen-yuan,CHENWei-rong,ZHANGXue-xia
(SchoolofElectricalEngineering,Southwest Jiaotong University,Chengdu 610031,China)
A scheme to value the control variableweights ofoptimalgenerator-shedding control for emergency control of power system transientstability is proposed in this paper.Since the inertia of power system would decrease because of generator-shedding,the power system transient stability level is changed.In this paper,the generator-shedding controlvariableweightsare regulated based on the influence of the inertia changing on the transientstability leveland linear programming theory.Then the control strategy obtained by calculation canmake the power system transient stability level raise after the control variables areweighted.Thismethod improves the resultof generator-shedding control,and its physicalmeaning is definitive.The effectiveness of regulating the control variableweights proposed in this paper isverified by the simulation resultsofNew Egland-39 bussystem.
transientstability;emergency control;optimal control;generator-shedding controlvariableweight;inertia time constant
TM712
A
1003-8930(2013)05-0054-06
赵振元(1986—),男,硕士研究生,研究方向为新能源应用与电力系统稳定。Email:zzyballack@163.com
2012-05-28;
2012-07-30
中央高校基本科研业务费专项资金科技创新项目(SWJTU11CX036)
陈维荣(1965—),男,教授,博士生导师,研究方向为新能源应用、智能监控技术、智能信息处理等。Email:wrchen@swjtu.cn
张雪霞(1979—),女,博士,工程师,研究方向为计算机智能、电力系统及其自动化。Email:zxxswjtu@gmail.com
——控制量的实时计算

