无刷直流电机状态方程系数矩阵的动态更新

杜鹏，谢俊

（南京邮电大学自动化学院，南京 210046）

无刷直流电机状态方程系数矩阵的动态更新

杜鹏，谢俊

（南京邮电大学自动化学院，南京 210046）

在无刷直流电机控制系统的仿真中如何快速动态地求解无刷直流电机的状态方程组是一个关键问题。在Matlab/Simulink环境中，利用C语言形式的系统函数来构建仿真模块，可灵活快速地实现复杂系统的仿真建模。把系数矩阵放在静态变量存储区，可直接修改状态方程组的系数矩阵，达到快速修改此系数矩阵的目的。另外，在每个仿真步长的输出阶段修改系数矩阵，达到了动态更新的目的。仿真结果表明，文中所提方法可快速实现无刷直流电机控制系统的仿真，并可方便地用于验证无刷直流电动机的控制算法和策略。

状态空间方程组；系统函数；无刷直流电机；仿真

在研究无刷直流电机的过程中，需要建立无刷直流电动机BLDCM控制系统的模型，并根据数学模型采用适当的仿真技术。为了研究控制算法的有效性和观察BLDCM的动态性能，在仿真中需要动态地求解状态空间方程，即动态地改变状态空间方程的参数矩阵。

文献[1-2]研究了如何使用Matlab/Simulink以及电力系统模块集来仿真BLDCM，虽然该方法使用方便运行稳定，但是电力系统模块集是封装好的，关键模块的工作机理不清楚，在验证控制器的控制策略时受到限制。而且所使用的解法器采用固定仿真步长，性能上的改进只能采用减小仿真步长来实现，而这又会极大地增加仿真所用时间。因此寻求在Matlab/Simulink中完全自己实现的并且具有相当精度的仿真模块，具有一定的意义。在这方面国内外诸多学者做了有益的探索。文献[3]利用有限状态机对电机的控制回路进行仿真，简化控制算法的验证过程，但其研究出发点仅仅是电机的控制部分，对仿真中相电流的控制没有特别考虑。文献[4]和文献[5]对无刷直流电动机的驱动和控制的工作过程进行了仿真，但是其着眼点主要在于控制系统部分，没有对仿真精度进行分析处理，忽略了换相电流的动态过程，不够准确。文献[5]采用系统函数对无刷直流电机本体及驱动电源部件进行仿真，由于没有使用C-MEX形式的系统函数，不能对相电流的动态过程做细致的控制。MEX从字面上看是Matlab和EXecutable两个单词的缩写，MEX文件是由C或Fortran语言编写的源代码，经Matlab编译器处理而生成的二进制文件，如果源文件是C，那么把生成的MEX文件称为C-MEX。在Simulink中可以使用C语言来编写可以直接调用的系统函数，这种由C语言源文件所编译生成的系统函数称作C-MEX S-Function （C-MEX系统函数）。文献[6]在仿真精度控制方面做了研究，考虑了换相电流的暂态过程，但是只进行了初步的分析，而且只考虑了从两相通电到两相通电的情形。另外，文献[6]没有使用C-MEX形式的系统函数，其对相电流的控制很难做到很精确。文献[7]使用C-MEX形式的系统函数实现了永磁同步电机的仿真，对于理解电机的控制和如何使用C-MEX形式的系统函数方面有借鉴意义。

综上，虽然对于无刷直流电动机的建模方面已经研究得很充分了[8-9]，但是在仿真部分，目前的仿真技术还不是很理想。本文实现了具有高精确度的BLDCM仿真系统（不是建模）。采用C-MEX系统函数来求解电机本体的状态空间方程组，可以动态改变方程组的系数矩阵。采用C-MEX系统函数执行速度快，且可以很方便地移植到以数字信号处理器为核心所构成的控制平台中，既能快速验证电动机的控制算法，又能快速建立控制器原型[10]。

1 电机本体的状态方程

三相无刷永磁直流电动机系统由控制子系统、驱动子系统和电动机本体三个模块组成。建模主要是指驱动电源和电机本体而言的。驱动电源有很多形式，本文中采用比较常用的恒压源的形式；所使用的电机本体的数学模型也是学术界普遍采用的，很多实际因素的考虑都是理想的。

电机本体的状态空间方程：

式中：x=[iaibwm，为状态向量；u=[vabvbc，为输入向量；T表示矩阵的转置，即x，u都是列向量；A，B分别为

电机三相定子绕组采用星形接法，三相绕组完全对称。ia，ib，ic分别是三相绕组的相电流，单位为（A），规定流进绕组方向为正；wm是转子的角速度，单位是（rad/s），规定转子逆时针加速转动wm为正方向；Rs是定子绕组的电阻，单位是（Ω）；vab是A相和B相之间的电压，单位（V）；vbc是B相和C相之间的电压，单位（V）；Ls是定子绕组的电感，单位为（H）；Φa，Φb，Φc分别是A、B、C相的磁链函数，为无量纲的物理量；p是极对数。

式中：ia，ib，ic产生电磁转矩，记Ta，Tb，Tc分别是A相、B相、C相绕组产生的电磁转矩，Te是三相绕组产生的总的电磁转矩，单位是（N·m），为正表示使转子逆时针转动。F是转子和负载的总的阻尼（摩擦）系数，单位是（N·m/（rad·s-1））；Tm是负载加在转动轴上的机械转矩，单位是（N·m），其方向定义和Te一致；θe是电位置角，单位是（rad）；J是转子及负载的转动惯量，单位（kg·m2）；ea，eb，ec分别为各相绕组的反电动势，以ea为例：

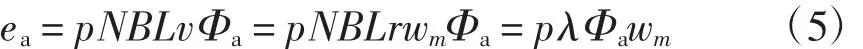
式中，λ=NBLr。注意在这里的N是一相绕组的边数，一相绕组可能包括多个线圈，都要算上（比如在4对极的电机中一相绕组一般有4个线圈，每个线圈有20圈，那么N=4×2×20=160）；B是永磁体产生气隙磁密，单位是特斯拉（T）；L是定子铁心轴向有效长度；r是定子内径；v是线速度（m/s）；λ是绕组每对极所产生的电动势的最大值。

2 状态空间方程的求解

考察状态空间方程，B矩阵仿真过程中保持不变，而矩阵A中有些元素固定不变另外的元素是和磁链函数Φa，Φb，Φc有关的，而Φa，Φb，Φc随着电位置角θe变化而变化，这就是说利用解状态方程的方法来仿真无刷直流电动机，必须动态地更新矩阵A。这样就牵涉到两个问题：（1）改变矩阵A，这种仿真方法得到的结果是否能够和数学模型相吻合；（2）如果能够，如何改变矩阵A才能高效地求解动态状态空间方程。下面就来解决这两个问题。

2.1 C-MEX系统函数的编写

首先简单地介绍C-MEX系统函数的结构，以及与Matlab/Simulink引擎和解法器之间的关系。这里只谈及本文涉及的部分，详细的内容请参考Matlab/Simulink相关帮助文档。

在C语言系统函数中主要有五个函数比较重要。第1，mdlInitializeSizes（SimStruct*S）函数完成系统函数的初始化工作，比如初始化结构体SimStruct，设置输入输出端口的宽度并检查不同模块间的连接是否合法、设置采样时间等。第2，mdlOutputs（SimStruct*S）函数用于计算连续时间系统或者离散时间系统的输出，对于连续时间系统的仿真输出值是状态x、输入u和时间t的函数。第3，mdlDerivatives（SimStruct*S）函数用于连续状态系统中动态方程的微分向量的计算，求解器利用此微分向量来进行实际的微分方程（组）的求解。微分向量是状态向量x的一阶导数，是状态x、输入u和时间t的函数。第4，mdlZeroCrossings （SimStruct*S）函数是C-MEX中特有的函数，用来帮助求解器确定一些关键的事件，比如某个状态信号或者输入信号是否过零。第5，mdlTerminate （SimStruct*S）函数在仿真结束时调用。

2.2 非线性系数矩阵的更新

矩阵A决定于转子的电位置角，电位置角是状态方程的一个状态，需要更新，在mdlOutputs（）中只要更新A矩阵即可。实现动态改变矩阵A的基本思想是，首先把A矩阵存入DWORK内存区（相当于C语言中的静态变量存储区）中，每次Matlab/Simulink引擎调用mdlDerivatives（）时，从DWORK中读入A矩阵和B矩阵。mdlOutputs（）在每一步运行都要更新A，即在Major和Minor中都要更新。随着仿真过程的推进，矩阵A相应地随着状态相电流和转子角度的变化而发生变化，这样就实现了动态的仿真。

从状态空间方程组来看，这样更新矩阵A是和理论值有差别的，缩短仿真步长是否可以把此误差减小，如果可以，仿真步长设定到多少才合适。对于梯形反电动势的BLDCM来说，Φa，Φb，Φc是电位置角θe的函数（虽然不能够表示为电位置角确定的简单函数，却是分段线性的，在仿真中比较容易生成）。在每一个换相状态中，Φa，Φb，Φc中只有一个值随着电位置角θe发生变化，而且和电位置角成线性关系。Φa，Φb和Φc在上升或下降变化期间（正好对应着一个换相状态），其对时间的导数和电角度θe（以及转子的位置角）也成线性关系，且转子的位置角和转子角速度wm都不可能突变。从这种线性关系可推断误差和仿真步长成反比，也就是说，减小仿真步长可有效减小误差，进而总可以减小仿真步长来使误差达到设定范围。由于现实中无刷直流电动机的转速最大数万转，换相状态维持时间最小在1/（24×100000）=4.17× 10-7s（以最大每秒10万转，4对极电动机为例），仿真步长设定和这个时间成线性关系，为它的百分之一可以接受的。当然这里的分析是定性的，实际仿真结果也可接受（见本文仿真结果部分）。

既然改变矩阵A能够和数学模型在任意小误差范围内相吻合，就剩下如何改变矩阵A的问题了。Matlab/Simulink设计环境中提供了用于求解状态空间方程组的模块，但其系数矩阵在仿真过程中不可改变，这对于仿真像BLDCM控制这样动态的系统是不适合的。在Matlab/Simulink中提供了求解此类问题的模块，但可惜的是，改变系数矩阵非常麻烦而且效率不高。有研究者提出了改变系数矩阵的办法，但已有方法效率不高。采用C语言的系统函数方式，可提高运算效率缩短仿真所用的运行时间。更重要的是C语言的系统函数提供了巨大的灵活性，使得仅仅在一个模块中动态改变系数矩阵成为可能。在C语言系统函数中，输出功能和微分功能是在不同的函数中实现的，输出时用到mdlOutputs（），微分时用mdlDerivatives（）。Matlab/Simulink引擎会在合适的时机调用这两个函数。实现动态仿真的具体步骤是：仿真开始阶段设定系数矩阵的初始值；在每一个仿真步长的微分阶段从静态变量存储区取回将要用到的系数矩阵A，进行状态更新；在每一个仿真步的输出阶段，改变矩阵A，并把它存入静态变量区中；接下来的微分阶段用到的正好是更新过的矩阵A；如此反复，就实现了动态更新系数矩阵。另外，矩阵A中实际需要改变的元素只有几个，所以可以利用这一点，只更新需要更新的元素以达到进一步减小运算量的目的，从而提高了矩阵A系数更新部分代码的执行效率。

3 仿真实现及结果分析

在Matlab/Simulink中搭建仿真系统时，需要Matlab/Simulink元件库中的模块来完成积分、微分、增益、加和、滞环控制、饱和限幅等功能。而利用C-MEX系统函数来实现仿真，只需四类基本模块：系统函数模块、Mux模块、Demux模块、用于给定参考信号的Step模块。其中最重要的是系统函数模块，Mux模块和Demux模块用于一个端口信号的复用和解复用，只是为了方便系统函数模块之间的信号互连的目的，Step模块用于给定负载参数等利于仿真的执行。图1是实现系统仿真结构图，分为控制器、驱动和电动机本体、输出模块。控制器用于控制电机的驱动电源，实现不同的控制算法和策略。输出模块中主要是用于信号波形的显示。如图2所示，驱动和电动机本体是密切联系的，放在一个Matlab/Simulink子系统中。为了验证相电压的控制效果，控制器中使用了比例型PID算法，实现了一个简单的速度控制环。

为验证整个系统的性能，设计了一个简单的比例型PID控制算法，对电机在动态改变负载转矩的性能进行了仿真。如图3所示，仿真中电机参数设定为：三相4对极，驱动电源Vdc=320 V，动惯量J=0.002kg·m2，Ls=2.72×10-3H，M=1.5×10-3H，N=50，定子内径r=0.04 m，定子铁心轴向有效长度L=0.2 m，永磁体产生气隙磁密B=0.816 7 T，阻尼系数为F=0.000 2 N·m/（rad·s-1）；极对数为p=4。仿真参数的设定参考作者所在实验室的一台电机，此电机的额定功率为2 kW，额定电压为500 V，额定转速为3 000 r/min，额定电流为10 A，最大瞬时电流为15 A。仿真中使用的电感和互感参数参考了此电机。

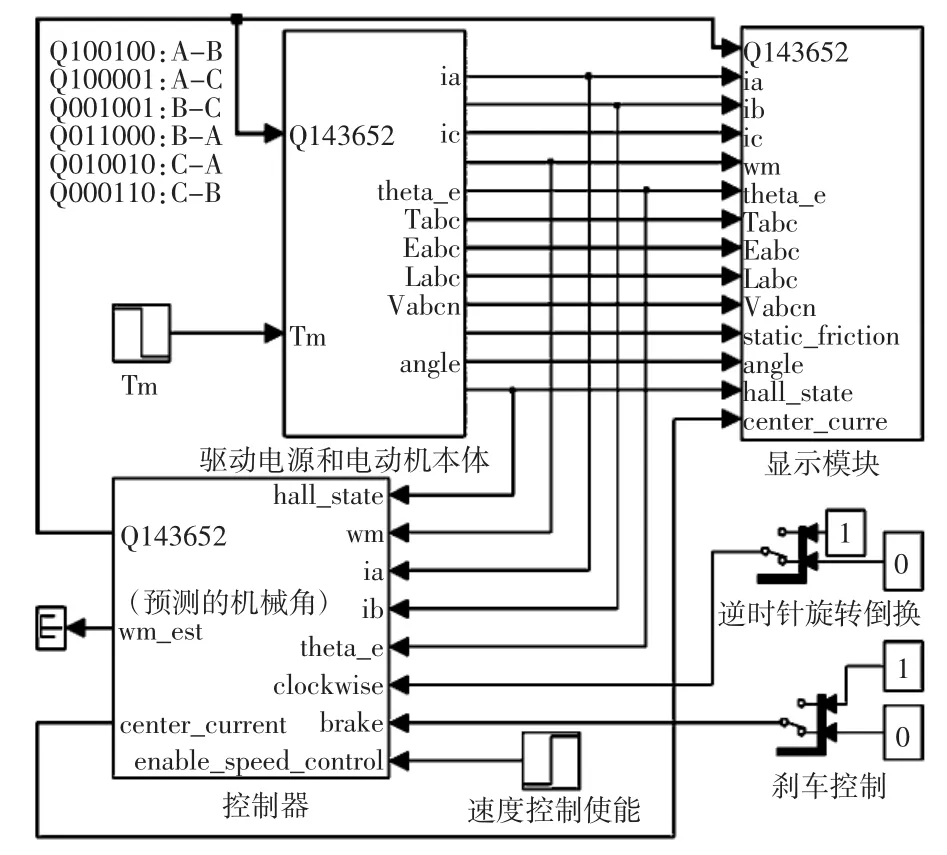
图1 电机控制系统仿真结构图Fig.1Simulation structural diagram for control system of BLDCM

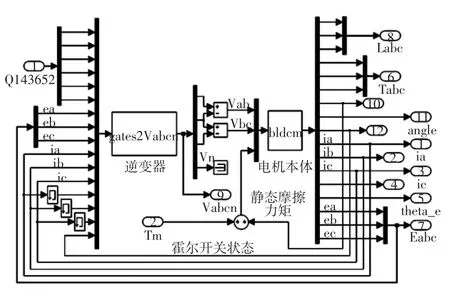
图2 驱动电源和电机本体仿真结构图Fig.2Simulation structural diagram for drive power source and body of BLDCM

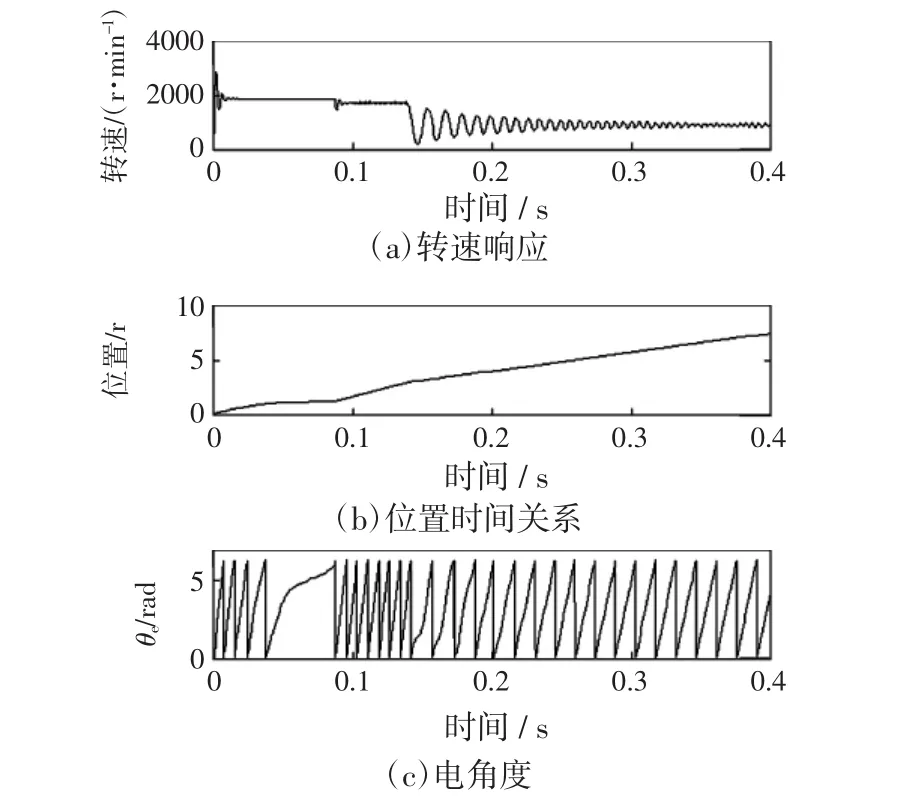
图3 速度环性能（使用简单的PI控制算法，给定转子转速为1 000 r/min）Fig.3Speed loop performance（with a simple PI algorithm，rotor speed being 1 000 r/min）

如图3所示，仿真开始负载转矩为零，在0.04 s时，加入10 N·m的负载转矩，速度环在0.06 s开始起作用，通过逐渐调整相电流，使转速逐渐回到1 000 r/s的转速，由于仅仅是采用简单的比例控制算法，在给定速度处有小幅震荡。

仿真结果表明，所提方法可使仿真结果在很高的精度上符合理论模型。采用该仿真架构可灵活地验证各种控制算法和控制策略，使用C语言的控制代码实现后可以直接用于DSP等实时控制系统中，加快了系统设计和开发，为分析和设计无刷直流电机控制系统提供了一个比较理想的实验和验证平台。

4 结语

在仿真部分，目前的仿真技术还不是很理想。主要表现在：①仿真型存在的计算效率低；②忽略换相点后电流动态变化及不够准确等问题；③控制系统的加入比较困难，且不实用。本文针对如上3点，实现了具有高精确度的BLDCM仿真系统（不是建模）。针对问题①采用C-MEX系统函数来求解电机本体的状态空间方程组，方程组的系数矩阵可以动态改变。针对问题②采用过零检测方法，帮助求解器来确定相电流的过零点，加上合理设置仿真步长，使得二极管的续流截止点可以精确定位。针对问题③使用C语言的系统函数执行速度快，因为是用C语言写成，可以很方便地移植到以数字信号处理器为核心所构成的控制平台中，既能快速验证电动机的控制算法，又能快速建立控制器原型。

在本文中换相方式是两相通电模式，在三相全部不通电时电流的变化和控制策略密切相关，经过分析和设计，本文实现的仿真方法还允许控制策略和算法中采用电流滞环的方式。但是BLDCM的驱动电源有多种形式，本文中实现的仿真是针对电压源型的，对电动机本体的模型也是非常理想的，这样实现的仿真其适用范围是受限制的。完全使用数值仿真的方法，必须要考虑到驱动电源的方式和BLDCM电机本体的建模方式，以及换相方式和控制策略的采用，进一步研究可以针对不同驱动电源形式、三相通电模式等。

[1]Hoang Le-Huy.Modeling and simulation of electrical drives using Matlab/Simulink and power system blockset[C] //27th Annual Conference of the IEEE Industrial Electronics Society，Denver，USA：2001.

[2]Zabalawis A，Nasiri A.State space modeling and simulation of sensorless control of brushless DC motors using instantaneous rotor position tracking[C]//IEEE Vehicle Power and Propulsion Conference，Arlington，USA：2007.

[3]王华斌，刘和平，刘平，等（Wang Huabin，Liu Heping，Liu Ping，et al）.有限状态机的无刷直流电机系统仿真分析（Simulation of a brushless direct current motor based on finite state machine theory）[J].重庆大学学报（Journal of Chongqing University），2008，31（11）：1307-1312.

[4]纪志成，沈艳霞，姜建国（Ji Zhicheng，Shen Yanxia，Jiang Jianguo）.基于Matlab无刷直流电机系统仿真建模的新方法（A novel method for modeling and simulation of BLDC system based on Matlab）[J].系统仿真学报（JournalofSystemSimulation），2003，15（12）：1745-1749，1758.

[5]钟君柳，姜孝华（Zhong Junliu，Jiang Xiaohua）.基于S-函数的无刷直流电机系统建模研究（Study on modeling of BLDCM control system based on S-function）[J]．微计算机信息（Microcomputer Information），2007，23（3-1）：273-275，263.

[6]解后循，高翔（Xie Houxun，Gao Xiang）.基于S-函数的无刷直流电动机自适应控制系统建模（Modeling and simulation of BLDCM adaptive control system based on S-function）[J].微电机（Micromotors），2009，42（3）：68-72.

[7]沈艳霞，薛花，纪志成（Shen Yanxia，Xue Hua，Ji Zhicheng）.基于CMEX S-函数直流无刷电机控制系统仿真建模研究（Study on modeling and simulation of brushless DC motor control system based on CMEX S-function）[J].中小型电机（S&M Electric Machines），2004，31（6）：10-14.

[8]Jeon Y S，Mok H S，Choe G H，et al.A new simulation model of BLDC motor with real back EMF waveform[C]// 7th Workshop on Computers in Power Electronics，Blacksburg，USA：2000.

[9]Pillay P，Krishnan R.Modeling of permanent magnet motor drives[J].IEEE Trans on Industrial Electronics，1988，35 （4）：537-541.

[10]刘贺平，汪芳君，张春梅（Liu Heping，Wang Fangjun，Zhang Chunmei）.基于DSP的直流无刷电机数字控制系统的设计（Design of digital control system for brushless DC motor based on DSP）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（1）：80-83.

Dynamic Update of State Space Equation Coefficient Matrix in Brushless Direct Current Motor Simulation

DU Peng，XIE Jun
（School of Automation，Nanjing University of Posts and Telecommunications，Nanjing 210046，China）

In control system simulation of brushless direct current motor，to solve state equations of the brushless direct current motor is a key issue.In Matlab/Simulink environment，using C language system functions to build simulation module can be flexible and can achieve fast simulation of complex system modeling.By putting the coefficient matrix in a static variable storage area，the coefficient matrix of the equation of state can be modified directly and quickly.Meanwhile，during the output stage in each simulation step，modification of coefficient matrix can achieve the purpose of dynamically updating the matrix.The simulation results show that the proposed method can achieve fast simulation of brushless direct current motor control system，and can be easily used to validate the control algorithms and strategies of brushless direct current motor.

state space equations；system function；brushless direct current motor（BLDCM）；simulation

TM341

A

1003-8930（2013）04-0068-05

杜鹏（1971—），男，博士，讲师，研究方向为电机拖动和电力系统自动化。Email：dupeng@njupt.edu.cn

2012-12-20；

2013-03-18

南京邮电大学引进人才科研启动资助项目（NY208049）

谢俊（1979—），男，博士，副教授，研究方向为电力系统优化调度与电力市场。Email：jxie@njupt.edu.cn