地震图像随机噪声的非局部均值去噪法

黄英，文晓涛，贺振华

（成都理工大学地球物理学院，四川成都 610059）

地震图像随机噪声的非局部均值去噪法

黄英，文晓涛，贺振华

（成都理工大学地球物理学院，四川成都 610059）

随机噪声的存在往往会影响地震图像分析的准确度。为了提高图像分析质量，提出了一种基于非局部均值滤波（Non Local Means）抑制地震图像随机噪声的新方法。在对滤波像素点去噪时，该方法分配给每个相似像素点的权重不依赖于2个像素点的空间距离，而是依赖以该像素点为中心的图像子块与以当前像素点为中心的子块之间的相似性，且滤波参数h的选取对滤波效果起到至关重要的作用。结合实例，对地震资料进行了具体分析。结果表明，与传统方法（如中值滤波、高斯滤波）相比，采用非局部均值滤波方法合成地震记录和实际数据时，既能有效地抑制地震随机噪声，又能较好地保留地震同相轴陡变处或同相轴弯曲处的边缘细节信息，具有实用性和有效性。

地震数据；图像处理；非局部均值滤波；随机噪声

0 引言

在地震勘探开发中，断层、通道和裂缝等结构特征及河道砂体等沉积特征是发现和描述油藏的基础，分辨和分析地震资料中这些特征具有重要的意义；然而，这些区域地质形态的复杂性导致其地震数据易受噪声干扰，很难准确描述其实际情况。如何压制干扰波、提高信噪比，是野外采集、资料处理及解释等都需要考虑的问题。随着勘探技术的发展，勘探目标逐渐向更深层和更复杂区域转移，这也给地震资料处理提出了更高的要求。

传统的地震资料去噪方法，如F-K域倾向滤波、中值滤波和高斯滤波等，容易产生平滑而丢失图像细节纹理信息的问题，甚至会引起大断层两侧同相轴的错误连接。非局部均值滤波NLM（Non LocalMeans）是目前一种能良好保持结构性能的去噪方法，可更好地保持地震图像边缘、纹理等特征。因其图像处理的效果显著，所以被成功应用于医学数据去噪、雷达数据去噪、语音与音频去噪、微缩复印去噪等领域。基于此，本文提出将其用于地震图像随机噪声去噪。

1 原理

非局部均值滤波是由Buades等[1]提出的，该方法只适用于对含有高斯滤波噪声的图像进行去噪。假设含随机噪音的图像像素ν被定义为

式中:u为最初不含噪音部分；n为随机噪音部分。

式中:W（i，j）为权重值，其大小由像素点i和像素点j的相似性决定。

注意图像中的任意像素点i对于其他像素点j都有1个独立的加权系数。为了计算像素点i和j的相似性，非局部均值滤波需要研究图像块Ni（以像素点i为中心的矩形邻域）的局部构造和纹理信息，然后利用像素点i和像素点j的相似性计算高斯加权欧几里德距离D（i，j），用来衡量像素i与j的相似度:

式中:ν（Ni）为图像块Ni中像素的矢量表示；a为高斯核标准差，a＞0；Ga为标准差等于a的高斯核函数；l为窗内nl个元素中的某一个元素。

对于二维图像，高斯核函数定义为

式中:x0和y0为元素l的坐标。

将高斯核函数与像素点i和像素点j的欧几里德距离相乘，窗内距离越远的像素点权值越小，这使得研究像素点附近的构造可尽可能地保留下来。已知像素点i与j之间欧几里德距离D（i，j），可以将i，j之间的权值计算式写为

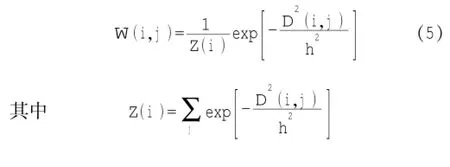
式中:Z（i）为归一化因子；h为平滑参数，用于控制权值相对于欧几里德距离的衰减程度。

当h值较大时，可对图像中所有像素点j计算出相似的权系数，而当h取值较小时，只会对一些像素点j算出一部分的权值。

非局部均值算法中，相似窗的形状和大小是不确定的，通常根据图像来定义；但是一般情况下，会选择矩形相似窗。像素点i与j的相似度与它们的邻域灰度向量ν（Ni）和ν（Nj）有密切关系[2]。

2 实际资料处理

2.1 h值的影响

非局部均值滤波的核心思想是，在1个大的搜索范围内（甚至整幅图像中），将与被滤波像素相似或匹配的像素点找出来，然后参与到滤波过程中，以实现更好的滤波效果[3-4]。

运用该方法滤波，滤波参数h值对滤波效果起关键性作用。当h值增强至极限时，会导致结果图像过于平滑，即产生过滤波现象，这容易使曲线过度平滑而丢失图像细节纹理信息，目标模糊；若h值选取过小，则会导致非局部均值算法不能够对图像去噪[5]。

为达到更好的滤波效果，可针对含噪图像平滑程度不同区域自动选取h值。具体操作是:当相似窗Ni内的纹理、边缘较多时，选取较小h值，便于对这些细节信息进行保护，从而避免滤波过度；当相似窗Ni内为平滑区域时，则应该选取较大h值，以便尽可能地抑制噪声。在提取图像边缘信息时，为了减少噪声对其影响，本文采用SUSAN边缘检测算法[6]，该算法不涉及梯度运算，具有很强的抑制噪声能力；为滤除孤立噪声点，则采用文献[2]，[7]中提出的方法。

图1为选取不同h值时非局部均值滤波对地震剖面图的滤波效果。图像数据来自KL深海区域的地震剖面，图像大小均为256×256像素，搜索窗大小为21× 21像素，相识窗大小为5×5像素。可以看出:当h取值不同时，去噪效果有明显的差异。当h=10时，非局部均值滤波几乎没有起到去噪作用（见图1b）；当h=200时，图像特性大部分消失，同相轴变粗，失去了去噪的意义（见图1c），这是因为完成非局部均值滤波是通过对比窗内像素点（或数据）与其他像素点（或数据）的相似性来实现的；当h=60时，非局部滤波对随机噪声起到了非常好的去噪效果，既很好地抑制了随机噪声,又很好地保持了图像特性（见图1d），相对很多传统去噪方法，表现出明显优势[8-11]。

图1 非局部均值滤波选取不同h值时的滤波效果

2.2 非局部均值滤波与中值滤波

中值滤波是一种去除噪声的非线性滤波，它充分利用了相邻2次中值滤波窗口内数据的相关性。

设Sxy为中心在（x，y）点，尺寸为N×M的矩形子图像窗口的坐标组，将这个窗口内各个像素按照灰度大小进行排队，g（x，y）为原灰度值，f（x，y）为得到的新的灰度，以代替中心位置灰度值，即:

式中:s，t为编程中时窗的元素。

目前图像处理一般采用中值滤波技术。该技术能较好地抑制噪声和保护图像边缘信息，然而在输入数据时，中值滤波仅考虑数据的排列信息，而不考虑数据的序源信息，从而导致图像处理中出现边缘抖动现象，且一些重要的图像细节也会消失。

相对于中值滤波，非局部均值滤波去噪后整幅图像去噪较均匀、效果好，且能将图像原有细节特征很好地保留下来，大大提高了信噪比（见图2）。因此，非局部均值滤波能很好地提高地震图像的质量。

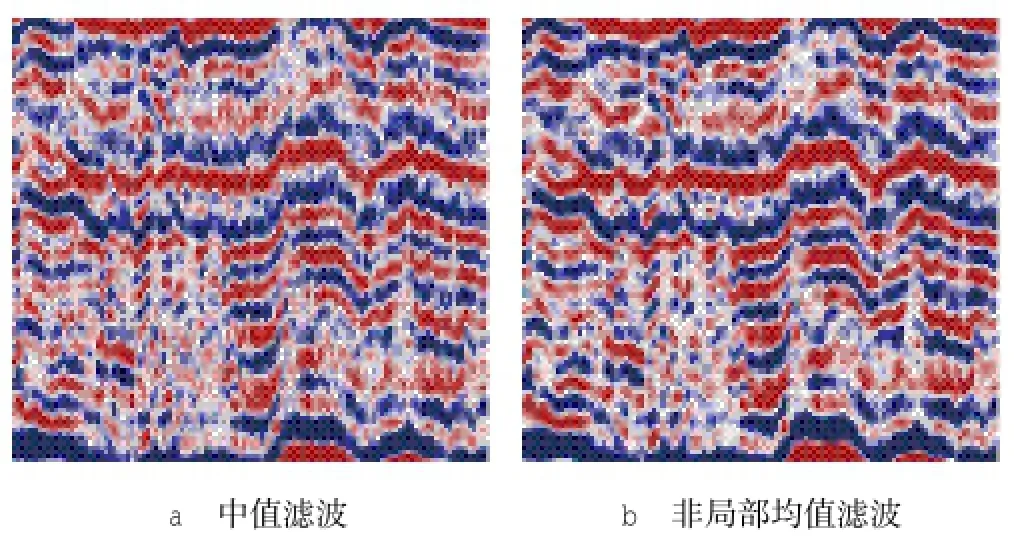
图2 非局部均值滤波与中值滤波效果对比

3 结论

1）非局部均值滤波通过利用地震数据的冗余度，有效提高了地震数据的信噪比，并最大限度地保证了地震资料的分辨率。

2）与其他常规的去噪方法不同，非局部均值滤波不会平滑掉图像中的小特征，如裂缝、小河道、断层等。

3）运用非局部均值滤波方法对KL地区的地震图像进行随机噪声处理，进一步验证了滤波参数h取值恰当与否，会直接影响图像处理效果的优劣。但本文方法存在计算时间过长的问题，仍需改进。

[1]BuadesA，CollB，Morel JM.Image denoisingmethods:A new nonlocal principle[J].SIAM Review，2010，52（1）:113-147.

[2]Buades A，Coll B，Morel JM.A review of image denoisingalgorithms，with a new one[J].Multiscale Modeling&Simulation，2010，4（2）: 490-530.

[3]Gleich D，Datcu M.Wavelet-based despeckling of SAR images using Gauss Markov random fields[J].IEEE Transactions on Geoscience and Remote Sensing，2007，45（12）:4127-4143.

[4]Espinoza Molina D，Gleich D，Datcu M.Gibbs Random Field models formodel-based despeckling of SAR images[J].IEEE Geoscience and Remote Sensing Letters，2010，7（1）:73-77.

[5]Wang Z，Bovik A C，Sheikh HR，etal.Imagequality assessment:From error visibility to structural similarity[J].IEEE Transactionson Image Processing，2004，13（4）:600-612.

[6]Smith SM，Brady JM.SUSAN:A new approach to low level image processing[J].International Journalof Computer Vision，1997，23（1）: 45-78.

[7]Zhang Y K，Zhang Y J，Lu H B.Statistical sinogram smoothing for lowdose CT with segmentation-based adaptive filtering[J].IEEE Transactionson Nuclear Science，1999，57（5）:2587-2598.

[8]张权，桂志国，刘袆，等.医学图像的自适应非局部均值去噪算法[J].计算机工程，2012，38（7）:182-185.

[9]周树道，王敏，叶松.利用小波域平滑和边缘保留的图像去噪算法[J].广西大学学报:自然科学版，2012，37（2）:307-311.

[10]易子麟，尹东，胡安洲，等.基于非局部均值滤波的SAR图像去噪[J].电子与信息学报，2012，34（4）:950-955.

[11]张权，罗立民，桂志国，等.一种基于优化参数的非局部均值滤波算法[J].计算机应用与软件，2012，29（3）:78-81，138.

（编辑 李宗华）

Denoising algorithm of random noisewith seism ic image based on nonlocalmeans

Huang Ying,W en Xiaotao,He Zhenhua

(College of Geophysics,Chengdu University of Technology,Chengdu 610059,Ch ina)

The presence of random noise tends to affect the accuracy of the image analysis.To improve the quality of seismic data, this paper putsup a new algorithm of random noise with seismic data based on nonlocalmeans.Thisalgorithm denoiseseach sample or pixel within an image by utilizing other similar samples or pixels regardless of their spatial proximity,making the process nonlocal.Filtering parameter h is importance for denoising random noise.Combined with examples,the seismic data are analyzed. The results indicate that the testswith synthetic and real data sets demonstrate that the nonlocalmeans algorithm does not smear seismic energy across sharp discontinuities or curved eventswhen compared to traditionalmethods such asmedian filter,Gaussian filter,which shows that the nonlocalmeansalgorithm isa practicaland effectivemethod.

seismic data;image processing;nonlocalmeans denoising;random noise

国家自然科学基金项目“裂缝性储层地震识别机理及相应方法研究”（41174115）；国家自然科学基金青年基金项目“基于复杂弱信号检测的礁滩相储层预测及油气检测技术研究”（40904034）；国家科技重大专项课题“南方海相碳酸盐岩层系大中型油气田形成规律与勘探评价（二期）”（2011ZX05005-003）

TE132

A

2013-05-06；改回日期：2013-09-06。

黄英，女，1978年生，在读硕士研究生，研究方向为图像处理。E-mail:hbkr9227@126.com。

黄英，文晓涛，贺振华.地震图像随机噪声的非局部均值去噪法[J].断块油气田，2013，20（6）:730-732.

Huang Ying，Wen Xiaotao，He Zhenhua.Denoising algorithm of random noise with seismic image based on nonlocalmeans[J].Fault-Block Oil&Gas Field，2013，20（6）:730-732.

10.6056/dkyqt201306012