重型燃气轮机压气机叶片气动弹性稳定性初期预判
张正秋,蒋洪德
重型燃气轮机压气机叶片气动弹性稳定性初期预判
张正秋,蒋洪德
(清华大学热能工程系,北京100084)
通过求解雷诺平均N-S方程并采用影响系数法,对某重型燃气轮机压气机叶片三个基本正交模态的叶片绕流问题进行了研究;同时结合有限元分析和稳定性参数分析,对压气机叶片气动弹性稳定性进行了初期预判。结果表明:以振型为判断标准的稳定性参数图,可作为压气机设计中气动弹性稳定性的预判工具;本文所述颤振稳定性初期预判方法,可为重型燃气轮机压气机气动弹性稳定性初期设计提供技术支持。
气动弹性;重型燃气轮机;压气机;稳定性参数;振荡叶栅;影响系数法
1 引言
寿命是衡量重型燃气轮机压气机叶片设计水平的重要参数。重型燃气轮机的工作状态变化虽不如航空发动机的剧烈,但由于其寿命设计要求的标准更高,不仅要在设计工作点和启动、停机过程中避免瞬态颤振的发生,还要有比航空发动机更为严格的高周疲劳(HCF)寿命要求。因此,随着压气机设计水平的不断提升,在设计点附近,对以小振幅极限环形式存在的颤振和强迫振动的抑制,将成为重型燃气轮机压气机设计中需要考虑的问题。
在典型压气机Campbell图上可看出,并非所有的燃气轮机EO线与固有频率线的交点都会发生共振[1]。这表明在工业领域中,燃气轮机用户不仅关心颤振及强迫共振的发生,更关心颤振及强迫振动条件下的振动幅值(振动应力),极低振动水平的气动弹性问题并不是决定HCF寿命的主要因素。由于决定气动弹性系统响应的关键因素是阻尼,其中气动阻尼水平的高低直接决定了保证结构安全所需的最小结构阻尼,因此研究叶片在固有模态振动下所对应的气动阻尼,对抑制HCF具有重要的指导意义。以近年ASME会议论文为例,气动弹性研究人员采用过多种不同复杂程度和考虑各种不同细节的气动弹性模型,来研究气动弹性问题[2~4],并揭示了多种气动弹性问题的物理本质,但由于计算量大,这类方法只能应用于详细设计阶段。由于初步设计阶段无法获得所有振动模态对应的气动阻尼,且无法摆脱叶片间相位角的束缚,导致气动弹性稳定性预测在工程上实现较为复杂。最早由Panovsky等提出的稳定性参数方法(国外也有研究人员称其为Tie-Dye法)[5],可用来计算不同折合频率下振型对亚声低压涡轮叶片颤振稳定性的影响,可应用于初步设计阶段的颤振稳定性设计。近年,笔者采用此类方法进行了系列研究工作[6~9],即采用稳定性参数法进行颤振稳定性预测,并将此方法发展到某航空发动机跨声风扇叶片的气动弹性稳定性研究中[10]。
本文以某重型燃气轮机压气机一、二级转子叶片为实例,结合有限元分析,将叶片模态振型表示在稳定性参数图中,并采用稳定性参数方法对其气动弹性稳定性进行初期预判。
2 算例说明及非定常计算结果
以某重型燃气轮机压气机一、二级转子叶片为研究对象,采用数值模拟方法对其进行气动弹性稳定性分析。计算模型如图1所示,图中给出了叶片的编号(-2叶片~+2叶片)和参考叶片0(运动叶片)的表面网格等。参考叶片的振动模态如图2所示,有轴向弯曲、周向弯曲和扭转运动,其中扭转运动的扭转轴位于前缘。参考叶片做简谐运动,且一级动叶振荡折合频率k为0.52,二级动叶振荡折合频率为0.37,其它叶片相对静止不动。压气机气动计算选择在设计点附近,非定常气动力分析采用稳定性参数法[11],详细的数值模拟方法参考文献[6]。

图1 某重型燃气轮机压气机动叶计算模型Fig.1 The computing model of a heavy-duty gas turbine compressor blade

图2 参考叶片振动模态示意图Fig.2 Blade vibration modal diagram
采用刚体运动假设。任意刚体运动扭转轴位置确定方法如图3所示,根据前、尾缘坐标和振幅计算刚体运动的扭转中心,微幅振动情况下扭转中心为前、尾缘振幅的中垂线交点。
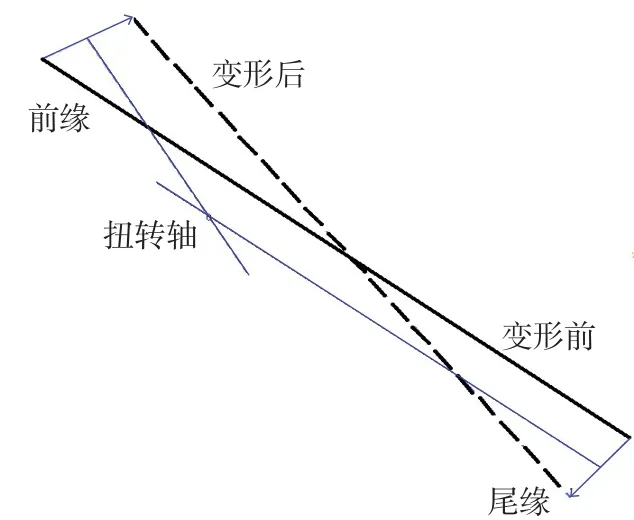
图3 刚体运动扭转轴定位示意图Fig.3 Rigid body torsional axis positioning diagram
非定常气动力采用一阶谐波振幅和相位的形式表示。为避免产生相位值大于360°的情况,相位值被限制在±180°范围内,因此+180°和-180°对应同一个角度。
图4所示为二级动叶轴向弯曲模态下,参考叶片及其相邻的±1叶片上,叶中截面的非定常气动力一阶谐波的幅值和相位在叶片表面的分布情况。图中横坐标表示叶片表面无量纲弧长,其中负值代表压力面,正值代表吸力面。从非定常气动力响应幅值分布看,压力面上气动力幅值相对较低,从前缘向后逐渐降低,接近尾缘时略有回升。吸力面上气动力幅值则相对较高,尤其是前缘及激波所在位置(定常分析表明,激波位于弧长为0.1位置)为非定常气动力的峰值区域,叶片表面上激波后气动力幅值逐渐降低,接近尾缘时又略有回升。三个叶片上气动力分布相似,但参考叶片上幅值最高,+1叶片上幅值最低。研究还表明,一级动叶在各个振动模态下的非定常气动力与二级动叶的类似。从分析结果可知,非定常气动力响应在跨声压气机中受激波的影响非常显著。

图4 二级动叶表面非定常气动力分布(轴向弯曲模态,k=0.37)Fig.4 Unsteady aerodynamic force distribution on stage 2 rotor blade(axial bending mode,k=0.37)
3 气动阻尼随IBPA的变化
图5给出了基本正交模态扭转分量对应的气动阻尼与叶片间相位角(IBPA)的关系,包括参考叶片和其相邻叶片(±1叶片)的贡献,以区分不同叶片对气动阻尼的贡献,同时也给出了三个叶片分量叠加所得的气动阻尼。之所以未考虑±2叶片的贡献,主要原因为数值结果表明,本文算例中非定常气动力主要分布在参考叶片和相邻叶片上,±2叶片上的非定常气动力贡献小到可以忽略,采用参考叶片和相邻±1叶片叠加所得结果,已可以较好地模拟行波振动下叶片表面的非定常气动力。
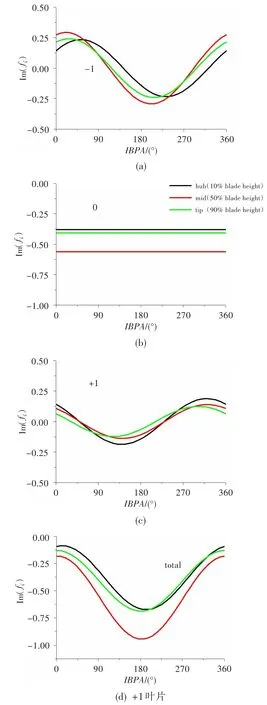
图5 三维气动阻尼随叶片间相位角的变化(二级动叶,扭转运动,k=0.37)Fig.5 The 3D aerodynamic damping changes withIBPA (stage 2,torsion mode,k=0.37)
从图中看,对于扭转振动,-1叶片上根、中、尖截面的气动阻尼幅值相差不大,但三个截面的相位明显错动,叶中和叶尖截面的最小气动阻尼位于200°附近,而叶根截面的最小气动阻尼位于250°附近。参考叶片上不同叶高方向也存在明显的三维效应,由于参考叶片的稳定性贡献不受IBPA的影响,因此为一水平直线,但其数值代表了参考叶片的气动阻尼水平。与端区截面相比,叶中截面气动阻尼的绝对值更大。相对于-1叶片,+1叶片上气动阻尼相位偏移也较明显,但幅值波动较小,这与非定常气动力的分析相符。其中叶根截面上的气动阻尼幅值最大,最小气动阻尼发生在135°附近。因此,在仅考虑参考叶片和其相邻叶片贡献的情况下,行波振动下气动阻尼随IBPA的变化为:根、中、尖三个截面上,气动阻尼表现出明显的三维效应,叶中截面的气动阻尼幅值较其它截面的大,各截面的最小气动阻尼对应的IBPA发生了偏移,这是三个叶片综合作用的结果。在其它模态下,气动阻尼随IBPA变化的规律有相似特征。分析表明,真实振荡叶片中三维效应明显,最小气动阻尼值和对应相位受三维效应的影响显著。
4 振型对颤振稳定性的影响
由于任意刚体运动都可用扭转运动表示,且任意刚体运动的非定常气动力都可通过基于三个基本正交模态的叠加获得,因此根据文献[9]所提出的方法,以扭转运动和弯曲运动为主的稳定性参数图如图6所示。图中横坐标和纵坐标表示二维叶片截面所在的平面,根据叠加理论,图中每个点都对应一种刚体运动,且每个点的数值都表示此刚体振动对应的气动阻尼。因此,当图中某点对应的气动阻尼为负时,表示该刚体运动模态下振动不稳定,且气动阻尼越小稳定性越差。另外,图中直线排代表叶片弦向和叶片周向排列方式,箭头表示叶片周向排列方向。
图6(a)中,参考叶片上游和下游均存在一个明显的稳定性参数区域,说明扭转轴位于此区域的振动将趋于不稳定;而与弦向近似正交的方向上则存在两个高稳定性参数区域,说明扭转轴位于此区域的振动将趋于稳定。图6(b)中,参考叶片在此图的中间位置,由于表示的范围较大,叶片大小已无法分辨,因此只用箭头示出了叶栅的排列方向。从图中可发现,远离参考叶片后稳定性参数分布关于原点中心对称。原因为相对于原点对称的两点所对应的弯曲振动相位差为180°,且距离原点正、负无穷的两点对应的是同一种弯曲模态。高稳定性参数和低稳定性参数区域基本呈正交方式分布。同时稳定性参数的梯度在空间上有明显变化,如扭转运动为主时参考叶片附近及上游的反“C”型区域,弯曲运动为主时稳定和不稳定区域的交界处等。在颤振稳定性设计中,若某刚体振动对应的扭转中心处于稳定性参数梯度较高的区域,应引起注意,因为此时振型的较小变化可能带来稳定性参数的较大变化。

图6 以扭转运动和弯曲运动为主的稳定性参数云图(一级动叶,k=0.52)Fig.6 The stability parameter contour dominated by torsion mode and bending mode(stage1,k=0.52)
通过对以扭转运动和弯曲运动为主的稳定性参数云图的分析发现,振型对稳定性参数的影响非常大,振型很小的变化都可能带来稳定性参数较大的改变,因此应将振型作为影响颤振稳定性的主要参数之一,这与笔者前期研究结果一致[9]。稳定性参数图独立于IBPA且物理意义明确,适合作为颤振稳定性的设计工具。
5 重型燃气轮机压气机叶片颤振稳定性初期预判
采用有限元法,对某重型燃气轮机压气机一、二级转子叶片进行模态分析,模态分析中考虑了离心预应力对模态的影响。表1示出了叶片前五阶频率和振型的计算结果。可见,一、二级转子叶片振型相似,前五阶振型分别为一弯、二弯、一扭、三弯、二扭,且随着阶数的升高,振型越来越复杂,振型的三维性也越来越强。
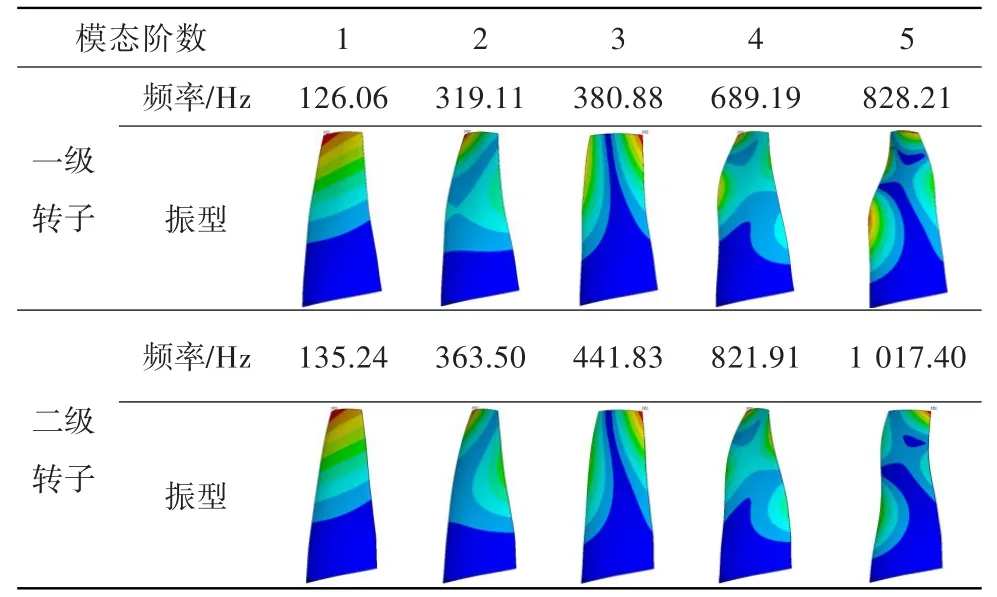
表1 转子叶片模态分析结果Table 1 The modal analysis results of the rotor blades
在刚体运动假设条件下,采用图3所示方法得到各阶模态对应的扭转轴位置,并将扭转轴位置在稳定性参数图上进行定位,即可判断该模态对应的稳定性参数,从而进行该模态下的气动阻尼预判及颤振稳定性预估。由于扭转轴位置较分散,无法清晰显示在同一幅图中,因此本文将在不同的显示范围内对分析结果进行描述。
图7所示为一级动叶叶中截面的分析结果。可见,一级动叶前五阶振型均较好地避开了稳定性参数最低的区域,但也没有落入稳定性参数最大的区域。尤其是四阶振型,处于稳定性参数梯度较高的区域,较小的误差都可能会引起稳定性参数较大的变化,应注意。
图8给出了二级动叶叶中截面的分析结果。可见,四阶模态落入了稳定性参数较低的区域,这表明在该模态下易引发不稳定的自激振动。Campbell图中,若在工作转速附近存在对应频率的EO激振线,则更应引起设计者关注,这表明有强迫共振发生的可能。解决方法为,针对特定模态,加入有效的机械阻尼来抑制振动幅值,必要时需在气动布局上进行调整。

图7 一级动叶叶中截面各阶模态稳定性分析(k=0.52)Fig.7 Mid span stability analysis of rotor blade stage 1(k=0.52)
通过前文研究可见,在压气机初期设计阶段,采用稳定性参数图并给予一定假设,可在工程可接受的计算量下,得出所有可能的刚体运动在所有可能的IBPA下对应的最小气动阻尼。这不仅为颤振稳定性分析提供了直接的参考依据,也为强迫振动等其它气动弹性问题研究提供了气动阻尼评估。与此相比,如果采用以非定常CFD及非线性有限元相结合的耦合或弱耦合法来研究气动弹性问题,几乎不可能完成;即使是在详细设计阶段或排故阶段,耦合方法的计算量及CFD分析的不确定度,也使得其难以应用于工程实际。
本文方法是基于三维计算的颤振稳定性准三维预判方法,即CFD及有限元分析均采用全三维计算,但气动弹性稳定性判断仍采用分截面的方式。不过由于高阶振型的三维性很强,不同叶高截面上准三维方法可能会得出相矛盾的分析结果;而由前文分析也知,真实叶轮机械中叶片的颤振稳定性存在明显的三维效应。因此,对于流动三维性不是很强的叶片,本文方法快捷、有效。但在真实叶轮机械环境中,尤其是风扇/压气机内部广泛存在的三维效应,可能对叶片的颤振稳定性产生重要影响。因此,在气动弹性稳定性详细设计阶段,需要有针对性地辅以全三维耦合设计方法。
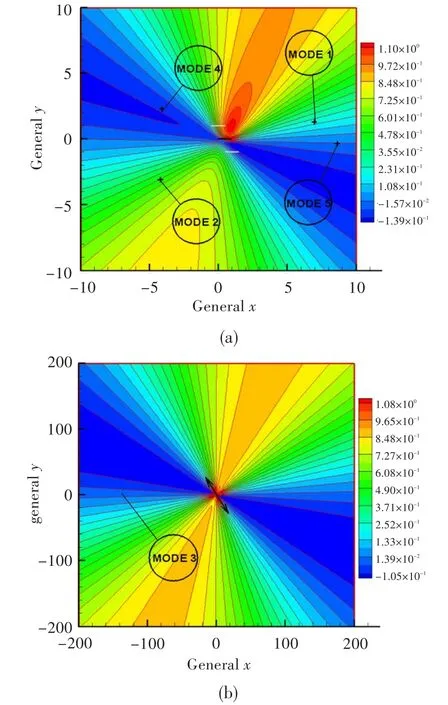
图8 二级动叶叶中截面各阶模态稳定性分析(k=0.37)Fig.8 Mid span stability analysis of rotor blade stage 2(k=0.37)
6 结论
(1)在跨声风扇叶片中,非定常气动力响应受激波影响显著,说明在跨声条件下,激波对系统的气动弹性稳定性具有重要影响。
(2)气动阻尼在叶高方向呈明显的三维效应,在详细设计阶段应考虑叶片通道内二次流及叶尖泄漏等复杂三维流动对气动弹性稳定性的影响。
(3)振型对颤振稳定性具有重要影响,可将其作为颤振稳定性设计的主要参数之一。
(4)本文方法可作为重型燃气轮机压气机叶片气动弹性稳定性初期预估方法,同时该方法也可为强迫振动提供气动阻尼预判。
[1]Marshall J G,Imregum M.A Review of Aeroelasticity Methods with Emphasis on Turbomachinery Applications [J].Journal of Fluids and Structure,1996,10:237—267.
[2]Peng C,Zilli A.A Methodology to Predicting Total Damp⁃ing of Axial Compressor Shrouded Stator Vanes[R].ASME GT2009-60359,2009.
[3]Srivastava R,Panovsky J,Kielb R,et al.Non-Linear Flut⁃ter in Fan Stator Vanes with Time Dependent Fixity[R]. ASME GT2010-22555,2010.
[4]Schoenenborn H,Chenaux V,Ott P.Aeroelasticity at Re⁃versed Flow Conditions:Part 1-Numerical and Experimen⁃tal Investigations of a Compressor Cascade with Controlled Vibration[R].ASME GT2011-45034,2011.
[5]Nowinski M,Panovsky J.Flutter Mechanisms in Low Pres⁃sure Turbine Blades[J].ASME Journal of Engineering for Gas Turbines and Power,2000,122:82—88.
[6]张正秋,邹正平,王延荣,等.三维振荡叶栅内部非定常流动数值模拟研究[J].燃气涡轮试验与研究,2009,22 (2):5—12.
[7]张正秋,邹正平,王延荣,等.进口气流角对三维振荡涡轮叶片非定常流动影响的数值模拟研究[J].燃气涡轮试验与研究,2010,23(1):15—21.
[8]张正秋,邹正平,刘火星,等.马赫数对振荡涡轮叶片非定常流动影响的数值模拟[J].热能动力工程,2010,25 (1):21—24.
[9]张正秋,邹正平,王延荣,等.叶轮机械颤振稳定性的工程预测方法[J].推进技术,2010,31(2):174—180.
[10]张正秋,邹正平,王延荣,等.叶轮机械颤振稳定性工程预测方法在跨声风扇中的进一步探讨[J].航空动力学报,2010,25(3):537—548.
[11]Hanamura Y,Tanaka H,Yamaguchi K.A Simplified Meth⁃od to Measure Unsteady Forces Acting on the Vibrating Blades in Cascade[J].Bulletin of JSME,1980,23(180):880—887.
Preliminary Aeroelastic Stability Design for Heavy Duty Gas Turbine Compressor Blade
ZHANG Zheng-qiu,JIANG Hong-de
(Department of Thermal Engineering,Tsinghua University,Beijing 100084,China)
Numerical simulation of 3-D unsteady viscous flow around oscillating compressor blades was carried out in the influence coefficient domain by resolving Reynolds average N-S equation.Combined with the FEM analysis and stability parameter analysis(Tie-Dye method),the aeroelastic stability analysis for compressor was done.The main results indicate that the stability parameter estimated on the basis of oscilla⁃tion mode could be a pre-evaluation tool for aeroelastic stability design of compressor.And the method pro⁃vides technical support for the preliminary aeroelastic stability design of heavy duty gas turbine compressor.
aeroelasticity;heavy duty gas turbine;compressor;stability parameter;oscillating cascade;influence coefficient method
V231.9
A
1672-2620(2013)02-0018-06
2012-10-09;
2012-12-14
张正秋(1979-),男,辽宁铁岭人,博士后,主要从事叶轮机械气动弹性问题的数值模拟研究。

