改进蜂群算法的旅行商问题仿真

苏晓勤，孙鹤旭，潘旭华

（1.河北工业大学 控制科学与工程学院，天津 300130；2.天津商业大学 信息工程学院，天津 300130）

0 引 言

旅行商问题（traveling salesman problem，TSP）由Dantzig等人于1959年提出，已被证明是NP难题的组合优化问题，很多文献中应用启发式算法求解，希望可以在短时间内获得更好的结果。多种优化算法用来求解TSP问题其中王忠英、白艳萍等［1］应用蚁群算法，Ilie、Badica［2］在分布式架构中提出分布式的蚁群优化算法，Kim和Cho［3］结合局部搜索的混合算法，另外还有文献使用了模拟退火算法［4］、遗传算法［5］，但都面临易陷入局部最优问题且算法的收敛性有待提高。蜂群算法是近几年新兴的优化算法，借助各个角色的分工合作与转换能有效改善优化问题。Whitfield［6］指出蜜蜂通过摇摆舞把食物源相关的方向和距离以及食物源好坏等信息传递给蜂巢中的其它蜜蜂。Karaboga［7］提 出了 人 工 蜂 群 算 法（artificial bee colony，ABC），并把ABC算法应用到解决TSP问题中［8］，其中跟随蜂的概率指定为固定值。Li－Pei Wong在文献［9］中利用“首选路径”的蜂群算法求解TSP 问题。胡中华、赵敏［10］利用ABC算法对TSP 问题进行求解。但上述文献都未考虑TSP问题求解的复杂度问题，求解大规模TSP问题时收敛慢、效果下降明显。

本文模拟蜂群觅食原理，应用改进的蜂群算法求解TSP问题，觅食寻优过程中蜜蜂动态转变角色；采用改进的局部搜索策略解决大规模基准测试问题，有效降低了TSP问题的复杂度。改进算法和传统算法对不同规模基准问题进行了分析对比，结果表明改进算法能有效地跳出局部最优，快速的收敛于最优解。

1 TSP问题

旅行商问题中一个商人必须访问n个城市。假设商人知道这一系列城市之间的距离（花费），规定商人必须访问每个城市有且仅有一次，最终回到他最初出发的城市，求出商人往返的最小距离或者花费。TSP 问题是用来确定哈密顿图中最小花费，被归类为NP难题的离散优化问题。

用城市间距离表示最小花费，城市间距离用式（1）表示，TSP问题路径长度f 由式（2）表示

2 改进蜂群算法

许多有趣的群体行为可以在一些动物诸如蜜蜂，蚂蚁，鱼等身上观察到。他们高度协调的觅食和聚集行为反映了这一现象。这些个体相对与整个系统来说，所能处理的问题是极其有限的，但是当把这些局部行为相结合时，将产生全局性的影响。

觅食过程中，蜜蜂记住形状、颜色和气味等食物特征，逐步形成自己的搜索经验［11］。在蜂巢附近搜索食物源的蜜蜂，通过摇摆舞把食物源的信息带回蜂巢，招募更多的蜜蜂进行采蜜。基于此共享信息，遗弃质量较差的食物源，调整搜索策略使得蜜蜂移动到质量好的精英食物源上，最终聚集于精英食物源。基于这个自然现象的启发，模拟蜜蜂觅食行为求解寻优问题。

2.1 蜂群的基本概念

蜂巢内共有三种蜜蜂：引领蜂，跟随蜂，侦查蜂；每种角色的蜜蜂分担不同的工作，相互协作，角色之间根据收益比在一定条件下进行相互转换。每个食物源代表一个解决方案，对应于TSP问题中的一条路径；食物源花蜜的收益就代表问题解的质量，对应于TSP 问题中路径质量，即路径长度的倒数。对于每个食物源来说，有若干个参数与之相关：食物源的花蜜（解决方案），花蜜的收益（解决方案的质量），花蜜的数量。

侦查蜂：探寻蜂巢周围的食物源，并且获取有关食物源的花蜜收益的信息，然后返回蜂巢，在舞蹈区通过蜜蜂独特的摇摆舞传达有关蜜源的信息。侦察蜂在算法陷入局部最优时能有效的跳出进行新食物源的侦察，跳出条件是蜂群在一段时间内没有发现更好的食物源，算法中利用食物源的遍历次数进行限定。

跟随蜂：在蜂巢的跟随蜂通过观察舞蹈区内有关蜜源的信息，依收益比决定是否跟随跳舞的蜜蜂采蜜。根据引领蜂的收益比自适应的决定跟随比，跟随蜂能加强引领蜂中的精英食物源的遍历，凸显引领蜂的精英作用，加速算法的收敛。

引领蜂：根据蜜蜂的收益比，决定引领角色。收益比高的蜜蜂，能招募更多的跟随蜂，使得算法快速收敛于最优。当食物源的花蜜被采集完毕时，引领蜂变为跟随蜂。

蜜蜂访问食物源时，若此食物源的花蜜质量优于这只蜜蜂先前的花蜜质量，则选择此处为新的蜜源，并返回蜂巢和其他蜜蜂分享食物源的信息，否则将保持先前的位置。倘若食物源在限定的次数内没有进一步提高，遗弃食物源。

2.2 路径选择与角色转换

蜂巢中最开始的蜜蜂都是侦察蜂，侦察蜂和跟随蜂按转移概率进行路径选择寻找食物源，转移概率的计算见式（3）

侦察蜂选择完路径，按收益比进行角色转换如式（5），收益比是侦察到的食物源质量与整个蜂群的食物源质量的比值，收益比越高意味着食物源质量越好，它应该招募更多的蜜蜂来采集蜂蜜

其中g 代表蜜蜂的总数，ibee 标识当前是哪只蜜蜂，fibee是当前第ibee 只蜜蜂的收益，与其经历的路径长度成反比。动态转变原则，见表1。

侦察蜂用来搜索新的食物源，每只侦察蜂对应一个食物源，它代表解的多样性，能帮助群峰跳出局部最优，但是个数过大会破坏优良路径，不利于算法的收敛，过小会使得搜寻新食物源的能力变差，经实验验证侦察蜂取蜂群总数的10%效果最好。

表1 动态转变原则

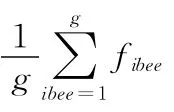
表2 跟随蜂的跟随比

2.3 算法描述

所需参数：MaxCycle－最大迭代周期数，Cycle－迭代周期数，Cn为蜂群中所有蜜蜂数即城市个数，Food＿Limit－允许访问食物源的最大次数，超过该数就遗弃食物源。Vn－食物源的访问次数，Best＿food－最好的食物源。

（1）GenerateInitRole（scout bee）／／算法开始蜂巢中的蜜蜂都是侦察蜂。

Scout＿bee（Cn）／／据式（4）计算路径的适应值ρij ，按式（3）计算Pij按概率选径，对找到食物源的访问次数Vn 进行累加。

Evaluate＿food（）／／对食物源的质量进行评价，得到最优食物源，计算收益比r见式（5）。

DChange＿role（）／／根据收益比r按表1动态转换蜜蜂角色。

（2）满足Cycle＜＝MaxCycle进入循环阶段

1）Leader＿bee（）／／引领蜂招募跟随蜂，访问食物源，Vn 进行累加。

2）Onlooker＿bee（）／／跟随蜂据跟随比按表2随引领蜂访问食物源，Vn 进行累加。

3）Scout＿bee（）

4）Evaluate＿food（）

5）DChange＿role（）

Vn ＜＝Food＿Limit重复步骤1），否则遗弃当前食物源，迭代周期数Cycle累加。

（3）输出最优食物源Best＿food。

3 改进局部搜索策略的蜂群算法

用局部搜索策略优化蜜蜂的解，可以加快算法的收敛度，针对一个蜜蜂所寻的食物源进行变换，将找到的质量更好的解替换原食物源，否则抛弃新解。Marco Dorigo在文献［13］中指出使用局部搜索策略可以大大减少循环次数，但是算法复杂度没有下降。

蜂群算法的复杂度为O（迭代周期数＊蜜蜂数＊城市数＾2），设置蜜蜂个数与城市个数相同，所以算法的复杂度为O（迭代周期数＊城市数＾3）。使用局部搜索后，可以大大减少迭代的周期数，但即使迭代周期数忽略不计，算法仍是O（城市数＾3）的复杂度。

采用改进局部搜索策略可以降低问题的复杂度，TSP问题中最优解的每个城市连接的都必定是附近的城市，即蜜蜂寻径时，只需要尝试附近的几个城市而不用尝试所有的城市。进行局部搜索时，不需要尝试跟所有其他连接的城市是否能交换出更好的结果，只需要尝试跟最靠近的若干个城市交换。把之前尝试的N个城市，变为尝试指定范围n（n＜N），提速N／n 倍，所以新的算法复杂度跟N 无关，只是一个常数，所以算法复杂度降低了一个数量级，成为O（T＊N＾2）。

对蜂群算法的精英路径进行改进的局部寻优，可以有效的降低算法的复杂性。改进局部搜索策略的蜂群算法解决TSP问题（ILSBCO）的流程如图1所示。

4 仿真结果

求解中国31个城市（Chn31）的最优路径，问题规模较小，不需局部搜索策略即可求得Chn31最优路径，参数设置为α＝1，β＝5，λ＝0.9，蜜蜂个数同城市个数，路径最大访问次数为10。在迭代到第50次即求得路径最优解，保留小数点后三位为15377.711，最优路径如图2所示。

利用国际上通用的测试问题库TSPLIB 中的几个TSP问题作为测试对象，城市的个数从70到493，利用基本的蜂群算法和改进局部搜索的蜂群算法对求解结果进行了对比分析如表3所示，可以看出在求解规模增大时，蜂群算法的性能急速下降，而改进的蜂群算法的求解随着规模增大也有不同程度的下降，但性能只是在很小的范围内下降。蜂群算法的参数设置为：最大迭代周期数设为1000，食物源的最大访问次数设置为100，蜜蜂个数设置为城市数。参数的设置为：α＝1，β＝5，λ＝0.9，三种角色按表1和表2描述的概率进行分配，改进的局部搜索策略中最近城市的个数设置为10。

针对基准问题pr299.tsp的求解与文献［15］中介绍的几个优化算法进行测试对比，性能分析显示无论是寻优时间还是最优解的误差以及平均解的误差结果中，取得了更好效果，见表4。

结果说明改进的蜂群算法能有效的使问题的复杂度降低，对于大规模的基准问题能取得更好效果，尽管得到的结果和设置的参数有很大关系，但这些可以通过实验求得。

表3 ILSBCO 与BCO 测试结果对比

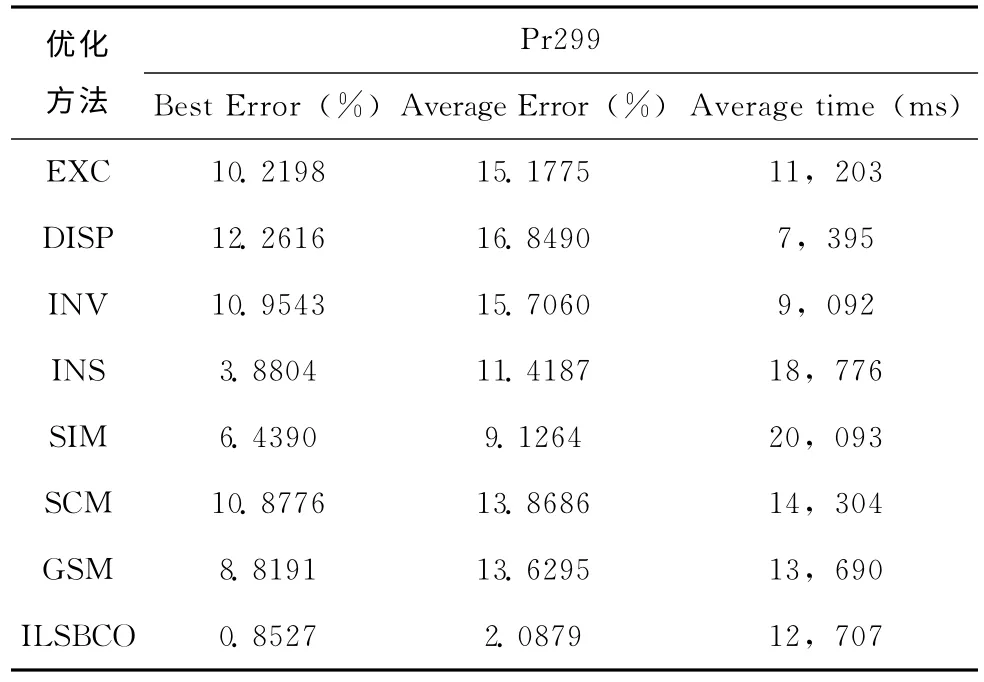
表4 不同优化方法测试Pr299的结果对比

5 结束语

基于蜂群觅食行为，三种角色蜜蜂相互合作，引进集体智慧，改进蜂群算法求解TSP 问题。根据收益比值利用引领蜂保留精英解，并动态招募跟随蜂保证算法的快速收敛，利用侦察蜂可以有效跳出局部最优问题，有效提高TSP最优解。针对大规模基准问题采用改进的局部搜索策略，降低求解问题的复杂度。改进蜂群算法与标准蜂群算法以及其它经典算法对不同规模基准问题进行测试，仿真结果表明改进算法在更短时间内找到最优食物源。

［1］WANG Zhongying，BAI Yanping，YUE Lixia.An improved ant colony algorithm for solving TSP problems［J］.Mathematics In Practice and Theory，2012，42（4）：133－140（in Chinese）.［王忠英，白艳萍，岳利霞.经过改进的求解TSP问题的蚁群算法［J］.数学的实践与认识，2012，42（4）：133－140.］

［2］Ilie S，Badica C.Effectiveness of solving traveling salesman problem using ant colony optimization on distributed multi－agent middleware［C］／／Poland：Proceedings of the International Multiconference on Computer Science and Information Technology，2010：197－203.

［3］KIM Y，CHO S B.A hybrid cultural algorithm with local search for traveling salesman problem［C］／／Korea：Proceedings of Computational Intelligence in Robotics and Automation，2009：88－192.

［4］QIAO Yanping，ZHANG Jun.Traveling salesman problem solving based on an improved genetic simulated annealing algorithm［J］.Computer Simulation，2009，26（5）：205－208（in Chinese）.［乔彦平，张骏.基于一种改进遗传模拟退火算法的TSP求解［J］.计算机仿真，2009，26（5）：205－208.］

［5］CHEN Minghua，ZHOU Benda.Solving traveling salesman problem using genetic algorithm based on Latin hypercube sampling［J］.College of Computer Mathematics Journal，2011，33（2）：138－144（in Chinese）.［陈明华，周本达.拉丁超立方体抽样混合遗传算法求解TSP 问题［J］.高等学校计算机数学学报，2011，33（2）：138－144.］

［6］Whitfield J.Animal behavior：The wisdom of the bees［J］.Nature，2010，467（7316）：658－659.

［7］Karaboga D.An artificial bee colony（ABC）algorithm for numeric function optimization［C］／／Indiana：Proceedings of IEEE Swarm Intelligence Symposium Indianapolis，2006：651－656.

［8］Karaboga D，Gorkemli B.A combinatorial artificial bee colony algorithm for traveling salesman［C］／／Istanbul：International Symposium on Innovations in Intelligent Systems and Applications，2011：50－53.

［9］WONG Lipei，Malcolm Yoke Hean Low.A bee colony optimi－zation algorithm for traveling salesman problem［C］／／Kuala Lumpur：Second Asia International Conference on Modeling ＆Simulation，2008：818－823.

［10］HU Zhonghua，ZHAO Min.Simulation on traveling salesman problem based on artificial bees colony algorithm［J］.Transactions of Beijing Institute of Technology，2009，29（11）：978－982（in Chinese）.［胡中华，赵敏.基于人工蜂群算法的TSP仿 真［J］.北 京 理 工 大 学 学 报，2009，29（11）：978－982.］

［11］LIU Yong，MA Liang.Bees algorithm for function optimization［J］.Control and Decision，2010，27（6）：886－890（in Chinese）.［刘勇，马良.函数优化的蜂群算法［J］.控制与决策，2012，27（6）：886－890.］

［12］CHONG C S，Malcolmlow Y H，Sivakumar A I.Using a bee colony algorithm for neighborhood search in job shop scheduling problems［C］／／USA：Proceeding of 21st European Conference on Modeling and Simulation，2007：1019－1025.

［13］Marvo Dorigo，Montes De Oca.Ant colony optimization［J］.Computational Intelligence Magazine，2006，1（4）：28－39.

［14］Bianchi L，Gambardella L.Ant colony optimization and local search based on exact and estimated objective values for the probabilistic traveling salesman problem［R］.Switzerland：IDSIA，2007：6－7.

［15］Albayrak M，Allahwerdi N.Development a new mutation operator to solve the traveling salesman problem by aid of genetic algorithms［J］.Expert Systems with Applications，2011，38（3）：1313－1320.