基于Z型结构的低存储二维DWT硬件结构
陶 钧,虞玉龙,沈海斌+
(1.浙江大学 超大规模电路研究所,浙江 杭州 310027;2.浙江杭州谷易科技有限公司,浙江 杭州 310000)
0 引 言
传统的信号理论是建立在傅立叶分析基础上的,但是傅立叶变换作为一种全局性的变化,有某些局限性,于是小波变换产生了。小波变换的优点是能够对信号进行由粗到精的多尺度分析,现在被大量不同的应用领域采纳,包括信号分析、图象处理、量子力学、理论物理、军事电子对抗与武器的智能化、医学成像与诊断、地震勘探数据处理、大型机械的故障诊断等方面,因此小波变换具有极高的研究价值。特别是在图像处理领域,其良好的时频局部特性和去相关能力使得小波变换得到了广泛的使用。
JPEG2000标准的核心变换技术就是离散小波变换[1](DWT)。通过VLSI实现DWT 运算需要尽量减少逻辑结构和存储单元,来获得较低的功耗和较小的面积。传统的离散小波变换采用卷积的模式,需要相对复杂的运算和大量的存储单元。于是Sweldens在1994年的时候提出了提升算法(Lifting Scheme),从而减少了二维DWT的运算复杂度,方便用于硬件的实现。但通常的实现方法是先进行所有行变换,然后进行所有列变换,这使得中间需要大量的存储空间来缓存行变换的结果(一般需要N*N的存储空间,N为图像行列数),并且行列运算串行进行,效率不够高。因此已经提出了不少新的VLSI结构来减少缓存单元和进行行列并行运算,比如基于行[2-4](Line-based)和基于块[5-6](block-based)等结构,但存储单元数量还是相对较大。特别是当处理的图像越大时,存储单元增多带来的芯片面积增长速度也越明显。
本文结合基于行和基于块的二维DWT 设计,采用一种新的Z型调度方式,使得整个过程能够行列并行运算,并且减少中间缓存单元数量,只需4N个中间存储单元就能实现二维DWT 运算。同时,采用16位带符号整数和16位小数精度,使得该设计支持1023级(10位)的灰度等级来满足数字高清晰度显示的需要[7],同时保证DWT 变换过程中的精度。
1 基于提升的DWT及部分参数的选择
1.1 小波提升系数的选择及其分解步骤
JPEG2000标准给出了两种双正交小波滤波器,CDF9/7(有损)和样条5/3(无损),对于自然图形来说,CDF9/7滤波器的压缩性能比5/3滤波器更好,本文就以9/7滤波器来展开介绍设计流程。
因为CDF9/7小波系数均为比较复杂的无理数,硬件的实现比较复杂,故而钟广军、成礼智等人提出了一组简单的LS9/7小波提升系数[8],如式1,并且通过实验表明采用CDF9/7和LS9/7小波提升系数分解图像的压缩性能几乎相同,但减少了硬件实现的复杂度

提升小波变换由3个部分组成:分裂,预测,更新。分裂指的是将输入信号分为奇偶两组数列Xo和Xe;预测是指针对数据间相关性,用Xe与预测算子P来预测Xo,用预测值与Xo的差值来代替Xo,d=Xo-P(Xe),d表示图像的高频细节。更新是指用细节信号来计算低频近似信号,S=X+U(d),通过两次预测和更新得到近似分量和细节分量。9/7小波变包含两次预测更新过程组成,如图1所示。

图1 9/7小波变换
9/7小波提升算法的分解步骤:

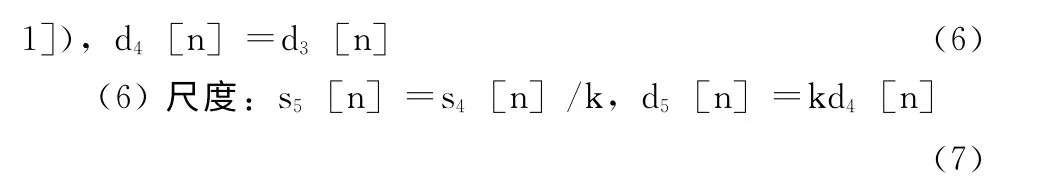
1.2 边界延拓算法
图像信号属于二维信源,一般受到物理约束而有边界,所以必须考虑它的边界效应,特别对于分解级数高的子带来说,一般对其采样数目较少,边界处理的好坏对于重建图像的影响比较大,因此一般需要进行边界延拓。
常用的边界延拓算法有边界元素复制法、周期延拓法、对称延拓法、0填充延拓法等等,其中边界元素复制法、0填充法的性能较差,一般使用周期延拓法或者对称延拓法[9]。对于图像处理,使用对称延拓法能得到比较平滑的图像边界,故而本文采用对称延拓法,其表达公式为式(8)
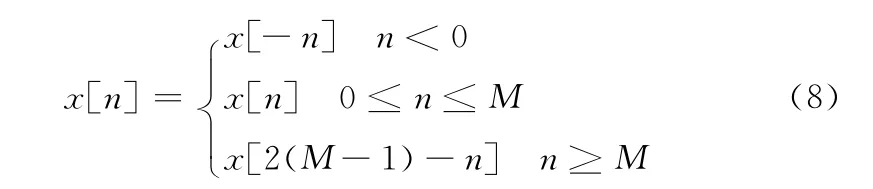
实验表明,当采用对称延拓算法进行5级小波变换时,图像恢复的质量相对较好。
1.3 定点长度的选择
硬件电路的数据运算有浮点和定点之分,浮点运算的精度较高,但相应的电路较复杂,速度也较慢,而定点运算则电路简单,速度较快。本文采用定点运算做DWT 运算。但定点运算必须先预估运算时中间值和结果的最大长度来避免溢出。
对于9/7滤波器来说,其低通滤波器的时域冲击响应系数之和为

假设一幅图像的最大灰度值为M,然后经过N 级的小波变换之后,其最低的子带系数(LL)有可能出现的MAX 值
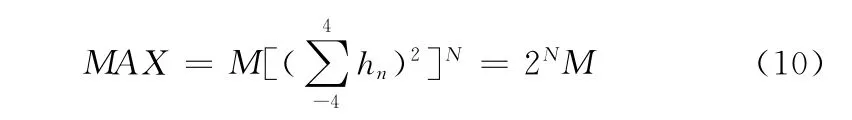
即,当N=5(5级小波变换),K=1023(10位灰度)时,Max=32736,所以此时需要15 位来存储小波系数的整数部分。目前常见的数字高清晰度显示可以达到10位以上的灰度等级,同时考虑硬件设计与外围设备的通用性,所以本文采用15 位来表示小波系数的整数部分。另一方面,小波系数的小数部分对低频子带的精确度影响较大,故而本文采用16位来表示小波系数的小数部分,来提高计算的精度,加上最高的一位符号位,本文采用32位来表示单个小波系数值。
2 DWT结构设计
2.1 一维DWT结构
由上一节中提升DWT的计算步骤可知,一维DWT的硬件结构一般可以分为图2并行运算,同时处理所有的输入信号和图3串行运算,每周期处理一对输入信号。由于存储器的端口问题,一般选取图3使用流水结构以节省硬件资源。

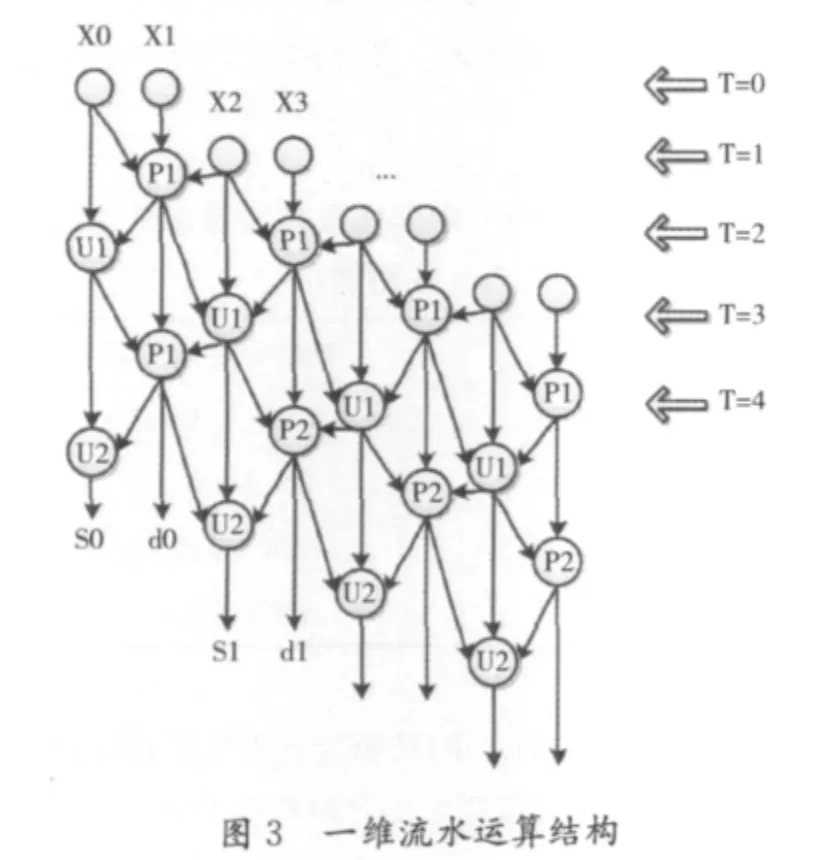
2.2 行DWT的硬件结构
由于本文设计的二维并行机制,使得行DWT 运算类似于基于行(Line-based)DWT的运行方式,故而采用较为常见的一种二输入的流水结构来作为行DWT 结构[10],具体结构见图4。
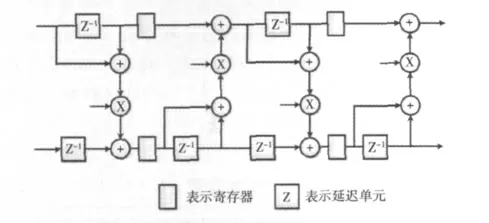
图4 行DWT的硬件结构
用一个寄存器来作为延迟单元,在图4中用z-1来表示,在该设计中需要8个加法器,6个乘法器(其中两个尺度变换时的乘法器未在图中标识)。每个周期送入两个数据进入流水线,由于并非是将一整行数据连续输入,所以按照一次输入两个之前保存的边界值然后下一次输入两个该行余下数据的方式运行,详见第3节中的具体描述。
2.3 列DWT的硬件结构
列方向的DWT 则是一个3 输入的流水线,如图5 所示。需要额外的SRAM 来存储上次计算过程中的边界数据,总计需要4N个存储单元。每次(第一次除外)有新的两个数据进入流水,再额外从SRAM 中读取对应的一个数据来进行计算,详见下一节中的具体描述。
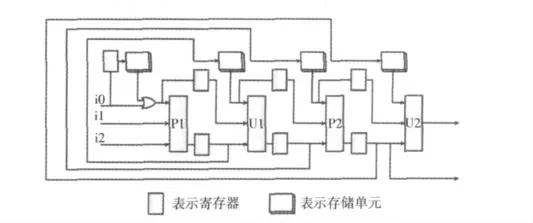
图5 列DWT的硬件结构
3 二维并行过程
普通二维DWT 计算过程在计算过程中需要存储大量的缓冲数据,会造成大量的硬件开销,所以本文提出了一种新的基于Z型结构的运行方法,老减少中间的存储单元,并且使得行列并行。
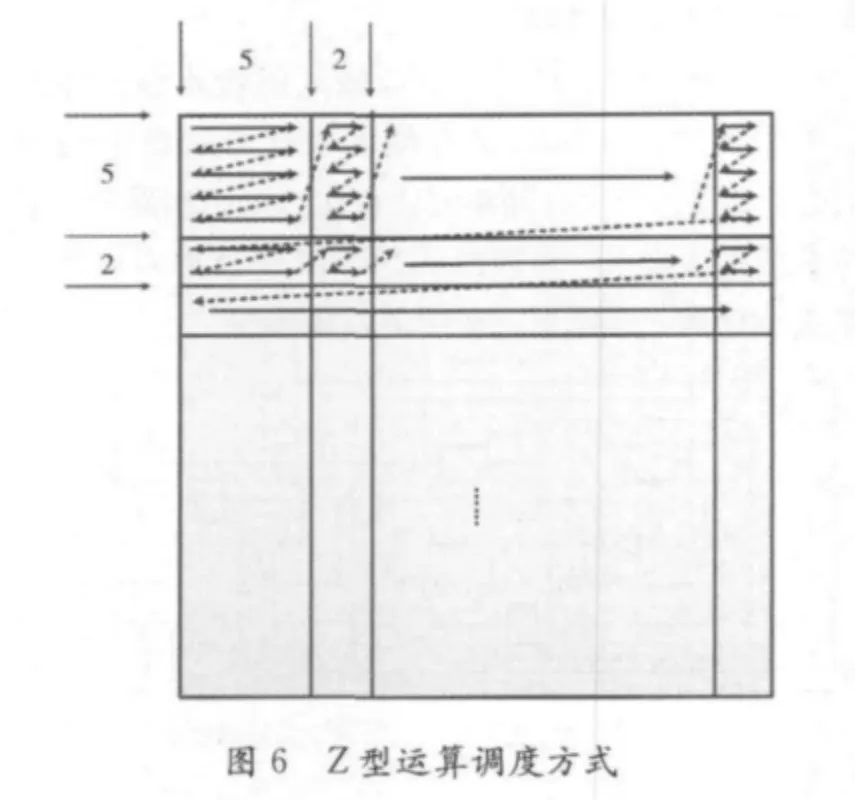
因为采用的是对称边界的方式,所以只需图像第一行的前5个信号数据就可以得到第一组2个小波系数,同理只要先完成前五行的第一组小波系数就可以开始列方向的DWT,故而如图6所示,本文提出的二维DWT 运行方式为首先对前五行的前5个信号进行运算得到列方向所需的两列数据,此时列方向的DWT 同时开始进行,然后行方向回到第一行继续得到两个数据,与之前保存的边界数据一起运算得到新的两个小波系数,再依次运算第二到第五行,从而得到列变换所需的下两列数据直到前5行信号都完成行变换后,从第6行开始行变换只需连续两行得到的小波系数就可满足列变换所需,由此可以实现行列的并行运算,提高运算效率。
在并行运行过程中,由于行列变换均不是连续进行的,所以行列变换均需要进行边界缓存,图7所示为行变换需要保存的边界值,图8所示为列变换需要保存的边界值。
由行变换的结构可知,每周期有两个图像数据进入流水线,采用对称结构的9/7小波变换只需要前5个数据即可计算得第一组小波系数(S0和d0),然后换行继续计算,故而需要保存其边界值。如图7所示,需要保存以黑色标记的5个数据。完成前5行的第一组小波系数计算后,返回第一行继续计算,将之前保存的X4、X5以及X6、X7按顺序送入流水,加上之前的边界数据即可算的第二组小波系数(S1和d1),并保存新的边界值。以此类推计算其他行系数。
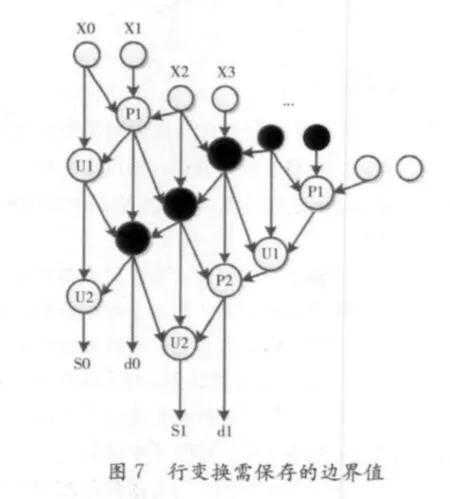
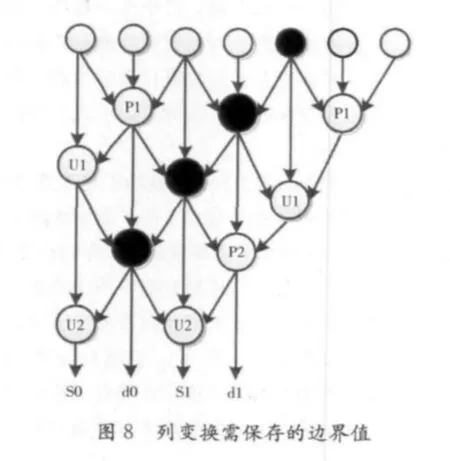
与行变换类似,由列变换的结构可以看出,每周期有三个数据进入流水线,故而当第一次5个数据完成运算后,每次将行变换所得的两个结果和之前缓存的一个值同时送入流水线进行操作,因此,需要缓存4个边界值,如图8中黑色标记的数据。
由图6、7、8可以看出,行变换的边界值保存需要5*5个寄存器,而计算N*N的一副图像则需要4N个存储单元来存储列变换的边界值,又由于列方向的处理速度要快于行方向,所以列方向的流水线并非时时有输入,故而可以使用单端口的RAM 来作为存储(4个单端口的RAM)。因为双端口RAM 面积要明显大于单端口RAM,这样可以有效较少芯片的总面积。然后还需要7*5个寄存器来存放行变换所得的小波系数提供给列变换进行运算。
表1与几个不同的二维DWT 结构的存储单元数量做了个比较,依照本文所述方法,可得到一个较少中间缓存单元的设计方法。

表1 不同二维DWT 中间缓存存储器需求的比较(N*N 图像)
当列变换完成后将LL的结果存放直外部存储器中,等待下一级分解,直到完成指定的分解级数为止。
4 实验结果与分析
基于本文提出的二维并行DWT 结构,进行了RTL 级Verilog代码的编写,并进行了代码仿真,验证了该结构的正确性和可实现性。由于该结构可以进一步加深流水线,可以较容易的提高系统运行频率,本文采用比较通用的100MHZ时钟对RTL进行DC综合。表1、2分别显示了当N=256和512 时,传统基于行的一种方法(一种非重叠的,基于2像素宽度图纹扫描的方式)和本文提供方法的面积比较,采用SMIC0.18um 工艺,100MHZ时钟,32位内部RAM,32位小波系数。
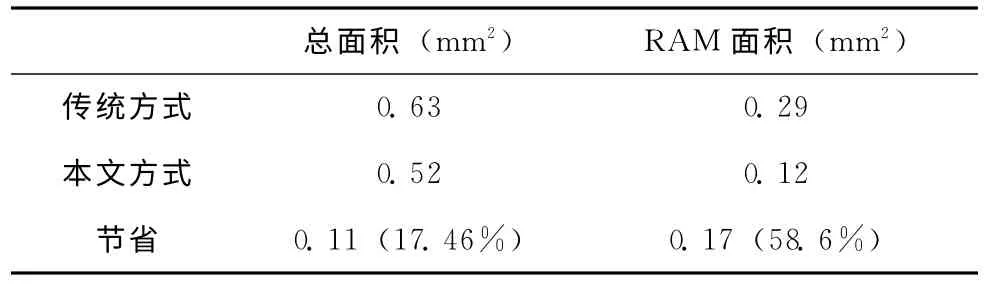
表2 与传统方式的比较(N=256)

表3 与传统方式的比较(N=512)
由表2和表3的数据可看出,实验结果与之前的结论相吻合,即依照本文的方法可以实现一种低存储(4*N 单端口RAM)的二维DWT 结构。并且当N 越大时可节省的面积越多,所以本文所提出的二维并行DWT 结构具有一定的优越性。本设计在100MHZ时钟下,每秒可以处理65帧1024*1024*10位的图像。
5 结束语
在目前的高清图像处理中,越来越大的图像尺寸需求必然使得芯片的片上存储不断加大,从而使得芯片的面积急速增加,节省片上存储空间将成为设计者必须面对的问题。本文提出了一种低存储的二维并行DWT 结构,并证明了其比较高效的运行速率和可实施性,行列运算都实现了流水操作,有较好的硬件利用率,并且使用了16位数据用于存放小波系数的小数部分,有较高的精度保证,该设计非常适合VLSI的实现。
[1]Smorfa S,Olivieri M.HW-SW optimisation of JPEG2000wavelet transform for dedicated multimedia processor architectures[J].Computers &Digital Techniques,IET,2007,1(2):137-143.
[2]WANG Chao,WU Zhilin,CAO Peng,et al.An effici-ent VLSI architecture for lifting-based discrete wa-velet transform[C]//Beijing:IEEE International Conference on Multimedia and Expo,2007:1575-1578.
[3]Jain R,Panda P R.An efficient pipelined VLSI architecture for lifting-based 2D-discrete wavelet transform[C]//New Orleans LA:IEEE International Symposium on ISCAS, 2007:1377-1380.
[4]PENG Cao,XIN Guo,CHAO Wang,et al.Efficient architecture for two-dimensional discrete wavelet transform based on lifting scheme[C]//Guilin:7th International Confe-rence on ASICON,2007:225-228.
[5]Yang C H,Wang J C,Wang J F,et al.A block-based architecture for lifting scheme discrete wavelet transform[J].IEICE Transactions on Fundam-entals of Electronics,Communications and Computer Sciences,2007,90(5):1062-1071.
[6]Salehi S A,Amirfattahi R.A block-based 2Ddiscrete wavelet transform structure with new scan method for overlapped sections[C]//Sharjah:Middle East Conference on Biomedical Engineering,2011:126-129.
[7]LU Chihwen,HUANG Lungchien.A 10-Bit LCD column driver with piecewise linear digital-to-analog converters[J].IEEE Journal of Solid-State Circuits,2008,43(2):371-378.
[8]DO Quan,Yo Sung Ho.Efficient wavelet lifting scheme based on filter optimization and median operator[C]//Danang:International Conference on Computing and Communication Technologies RIVF,2009:1-6.
[9]HONG Qi,WANG Kanwen,CAO Wei,et al.A reconfigurable VLSI structure for DWT[C]//Nanjing:International Conference on Information Science and Engineering,2009:465-468.
[10]Hannu Olkkonen.Discrete wavelet transforms algorithms and applications[M].Rijeka:Intech Open Access publisher,2011:41-56.

