基于GA理论的Volterra核辨识的多音激励设计

韩海涛，谭力宁，马红光，朱晓菲，杨东东

（1.第二炮兵工程大学701教研室，陕西 西安 710025；2.第二炮兵工程大学101教研室，陕西 西安 710025）

0 引 言

Volterra级数是非线性系统建模的重要工具，其Volterra核辨识是一个复杂和困难的问题［1］。Volterra核辨识对激励信号选择有严格的要求，如果激励信号选择不当则激发不出系统的特征，不能准确地对Volterra核进行辨识。传统Volterra核辨识方法往往采用高斯白噪声作为系统激励，通过时域自适应学习的方法来辨识Volterra核，这种方法存在的问题是，首先是产生高斯白噪声激励对设备硬件要求比较高，其次辨识出的核是局部有效的［2］。基于多音激励法的系统辨识为Volterra核辨识提供了一条便捷方法，然而该方法对多音激励信号的频域成分的选择以及相位都有的要求。文献［3］仅从频率成分的选择方面进行了论述，然而多音激励信号的相位也是一个必须考虑的重要因素，本文拟加入相位因素考虑多音激励信号的设计问题。

多音激励信号可以很好地激发出系统的动态特性，是一种广泛使用的测试激励信号［4－7］。多音信号是由在一定频带范围内的多个正弦信号叠加产生。但如果没有合理的选择相位，多个正弦信号的叠加会造成多音信号在时域上出现很强的波峰，这种现象的出现对系统测试是不利的，一是系统对激励信号的幅度有限制要求，如果波峰超过系统的响应范围可能会对系统产生损伤以至于破坏系统结构，还有可能人为的引入一些非线性因素；二是使系统的信噪比SNR（signal－to－noise ratio）下降，使测试容易受测量误差的影响。测试过程中对于干扰噪声的敏感性与测试信号的SNR 成反比［8］，因此提高测试信号的SNR 是提高测量精度的有效手段。波峰因子CF（crest factor）是衡量多音激励信号性能的一个重要指标，CF 越大说明多音激励信号的波峰就越明显。降低多音激励信号的CF 可显著提高信号的SNR，在不改变多音激励信号频谱特征的情况下如何降低多音激励信号的CF 是多音激励信号设计中面临关键的问题。目前这一问题还没有得到有效解决，是国内外学者共同探讨一个热点问题［8－13］。

文献［8］基于无穷范数提出了一种构造多音激励信号相位的方法，可以有效降低CF；文献［9］依据多音激励信号中每个频率成分的功率，选定该频率成分的相位及持续的时间，然后将多个时间段的信号叠加来构造多音激励信号，在一定程度降低了CF；文献［10］提出了一种时频域结合的方法来进行多音激励信号相位的选取，该方法首先从频域上构造多音激励信号的频谱，选定多音信号的频率成分及初始相位，其次对构造出来的信号频谱求反傅里叶变换得到时域信号，然后对时域中出现的波峰进行裁剪，并对裁剪后信号作傅里叶变换，校正多音激励信号的幅度及相位，以此达到降低多音激励信号CF的目的；文献［11］采用了多相互补码对的方法研究了多音信号峰值因子的减少作用；文献［12－13］将多音激励信号相位的选择看成一个求解最优化问题，采用随机尝试法和遗传算法来解决该问题，获得比较理想的实验效果。然而目前存在的方法使CF 降低的同时，使多音激励信号的功率谱有所失真不利于系统辨识。本文以Volterra核辨识的多音激励设计为目的，从多音激励信号的频率成分和相位两个因素考虑，采用优化遗传算法方法解决多音激励信号的相位选择问题，经实验结果验证该方法可以有效降低多音激励信号的CF，保证信号的功率谱不失真。

1 问题描述

1.1 Volterra级数

对于任意连续的时不变弱非线性动态系统，可以用N阶Volterra级数近似描述

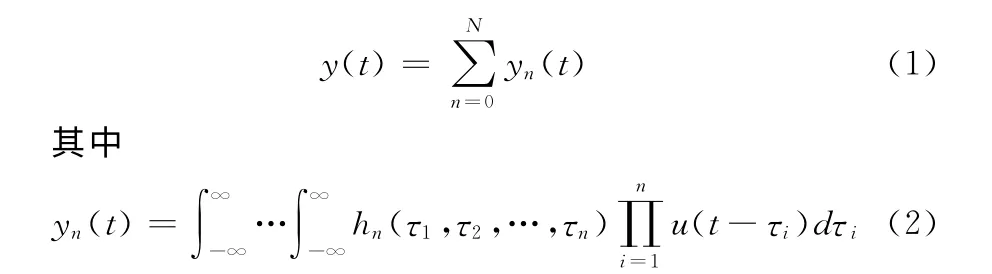
式中：yn（t）——系统的第n阶输出响应，hn（τ1，τ2，…，τn）——第n阶Volterra时域核，或称广义脉冲响应函数。hn（τ1，τ2，…，τn）的多维傅立叶变换为

Hn（ω1，ω2，…，ωn）称为非线性系统的第n 阶Volterra频域核，或称为第n阶广义频率响应函数GFRF（Generalized Frequency Response Function）

1.2 多音激励信号设计的约束条件

K 音的多音激励信号可用式（4）表示

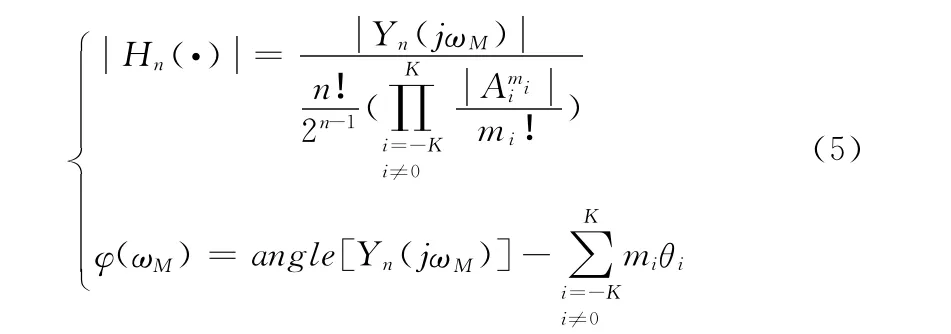
式中：Yn（jωM）——yn（t）的傅里叶变换中频率成为ωM的分量，φ（ωM）——Hn（ω1，ω2，…，ωn）的相位，angle——提取相位的函数。

波峰因子CF 定义为

Volterra核辨识的多音激励信号必须要满足两个条件，如式（8），条件一是同一阶核对应输出的频率成分没有重复，条件二是θi在0到π选取合适的值以使CF 最小

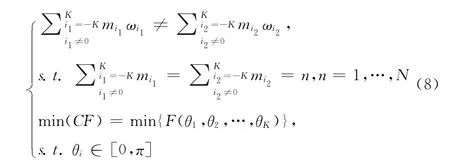
2 多音激励设计

关于Volterra核辨识多音激励信号频率成分的选择问题，已经在文献［3］中进行了论述，本节主要针对多音激励的相位的选取问题进行讨论。Schroeder法［9］是最早提出的降低多音激励信号波峰因子的方法，后来的改进方法都是按此方法的思路进行设计。

2.1 Schroeder法

Schroeder法是一种有效的多音激励信号相位的选取方法，可以使CF 得到很大幅度地降低，设计出来信号如式（9）所示

式中：T——周期，N——多音激励信号r（t）频率成分的个数，tk可按式（11）计算

那么r（t）瞬时相位为

由式（10）和r（t）的连续性可得

可以看出Schroeder法的特点是对多音激励的频率和幅度都有确定要求，即频率和幅度不能随意选取。这一特点也是该方法的缺陷，显然通过这种方式设计的多音信号不能用于Volterra频域核辨识。

2.2 基于遗传算法的多音激励信号设计

2.2.1 遗传算法

遗传算法（genetic algorithm，GA）是将生物学的遗传进化原理和最优化技术相结合的产生，它以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部的染色体的随机信息交换相结合的高效全局寻优搜索算法［14］。GA 将待解决问题的参数按照一定规则编码，由若干基因组成一个染色体，对群体进行选择、交叉和变异运算，经过多次重复迭代直至得到最后的优化结果。遗传算法需要解决以下问题：

一是编码问题，即如何将待求解的问题用一定编码规则来表达，这是GA 理论的基础，基本的编码形式有二进制码、格雷码、浮点数码、多参数级别联编码及多参数交叉编码等，编码应满足完备性、健全性和非冗余性等规范。二是选择算子的实现问题，选择算子是在群体中选择生命力强（即适应度高）的个体产生新群体的过程，这样使群体中适应度高的个体得到保留和发展，适应度低的个体逐渐被淘汰。选择算子应恰当，如果选择不当会导致算法早熟。三是交叉算子的实现问题，交叉算子是以较大的概率从群体中抽选两个个体的染色体，交换染色体的某个或某些位，该算子决定了GA的全局搜索能力。交叉运算包括交叉点位置的确定问题和部分基因交换的实现问题两个方面的内容。交叉运算可分单点交叉、两点交叉、多点交叉、均匀交叉与算术交叉。单点交叉与两点交叉的实现如图1所示。三是变异算子的实现问题，该算子是以一个小概率对个体染色体编码串上的某个或某些位值进行突然改变。变异是产生新个体的有效手段，其可以有效改善遗传算法的局部搜索能力和维持群体的多样性；四是是适应度函数的实现问题，其适应度决定个体遗传到下一代的概率。适应度函数是评价群体中各个个体在优化算法中能达到或接近最优解的优良程度，其设计应满足单值、连续、非负、最大化、合理、一致性、计算量小及通用性强等原则。

此外还应合理的选择GA的控制参数如：群众规模N、编码长度、交叉概率Pc和变异概率Pm等，这些控制参数的选择决定着GA的性能。群体规模N的大小直接影响到遗传算法的收敛性或计算效率，一般在10～200之间选取，交叉概率Pc一般取值范围为0.4～0.99，变异概率Pm一般取值范围为0.0001～0.1。

2.2.2 算法设计

基于多音激励的非线性系统的Volterra核辨识，首先需要确定多音激励信号的频带范围，通常的做法是对待辨识的非线性系统进行扫频分析，确定系统有效频率响应范围；其次在带宽响应范围内以同一阶输出频率成分不重合作为选择标准进行频率搜索，设搜索出的频率成分组成的集合为WM；最后确定WM中每一个频率分量的相位，使WM对应多音激励信号的CF 达到最小。

图1 交叉运算

以CF 最小化作为目标函数，如果多音激励含有K个频率分量，那么可将CF 看成含有K个变量的函数，如式（7）所示，θi（i＝1，…，K）在0到π 之间取值使CF的取值最小。将变量θi按一定规则进行编码，形成一个基因，将K个基因组合在一体形成一个染色体。随机生成一个种群，群体的规模为N，该群体按照选择、交叉、变异等运算进行进化，该流程可用图2表示。

图2 遗传算法实现流程

基于Volterra 核的多音激励信号设计可按以下步骤实现：

步骤1 对待测试系统进行扫频分析确定有效频率响应范围B，在B 内通过文献［3］提出的方法搜索多音激励信号的频率成分，频率成分组成的集合为WM，如果WM频率成分的个数为K，确定式（7）中变量的个数为K，转到步骤2；

步骤2 确定遗传算法的控制参数，如群众规模N、编码规则、交叉概率Pc和变异概率Pm，转到步骤3；

步骤3 初始种群由式（7）中每个变量在0到π 之间随机取值产生。后面种群的规模和个体差异均由进化规律决定，转到步骤4；

步骤4 以式（8）中条件二作为目标函数，对种群进行适应度评价。按编码规范进行编码，对种群中每个个体进行编码，多个变量对应的编码组合形成染色体；

步骤5 根据每个个体适应度，对种群进行选择操作。为了提高整体和局部搜索能力，分别对群体进行交叉和变异操作，转到步骤6；

步骤6 算法进化是否满足收敛条件，或者进化次数是否满足设定的次数，如果满足条件则输出结果，反之转到步骤3。

3 实验验证

通过两次实验验证本文提出的方法，实验一为仿真实验，和文献［3］提出的设计方法进行了对比；实验二是通过对一非线性模拟电路的多音激励信号进行设计，验证提出方法的有效性。

实验1Schroeder法设计的多音激励信号如式（9）所示，假设有16个谐波分量，如式（14）所示

如果将θk都设为0，得到多音激励信号和功率谱如图3所示，从图3（a）中可以看出相位为0时，激励信号产生尖峰很大，达到2.5V，经计算CF为5.101；采用Schroeder法，按照式（13）选择θk，得到信号和其功率谱如图4所示，从图4（a）中可以看出激励信号平滑，产生的波峰比较小，CF为1.620，但从图4（b）中可以看出，与图3（b）比较，Schroeder法设计出多音激励信号功率谱失真严重；如果采用本文提出的遗传算法得到的结果如图5所示，从图5（a）可以看出产生的多音激励信号没有产生很强波峰，信号比较平滑，CF为1.247，图5（b）与图3（a）相比较可以功率谱几乎没有失真。从而可以看出本文提出的方法在降低CF的同时，信号功率谱没有失真，从而验证了该方法的有效性。

实验2 图6为一非线性模拟电路，u为输入激励信号，流过R1电流为i1，流过R2的电流为i2，由于R2与C1并联，它们两端的电压同为u1，u1为系统输出，非线性电阻R2的伏安特性为：i2＝0.001（u1＋5u12），电路对u 幅度要求为5V。

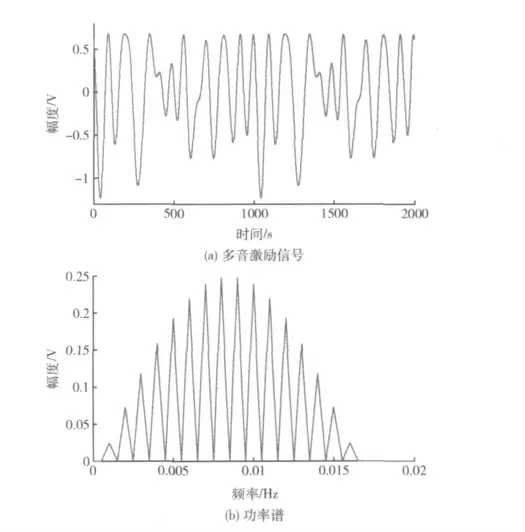
图5 遗传算法设计多音激励信号及其功率谱

图6 非线性模拟电路

采用文献［3］提出的方法设计出多音激励信号的频率，结果为WM＝｛11，511，1013，1517，2025，2553，3093｝Hz，WM中每个频率分量幅度选为1，采用本文提出方法进行相位选择，优化出的相位为｛－1.693，－3.008，2.548，0.744，－0.456，0.277，－3.086｝rad，未经优化的激励信号如图7（a）所示，其幅度已经超过5V，对应的CF为3.300，优化过的激励信号如图7（b）所示，幅度控制在了4幅度以内，对应的CF为2.133。

4 结束语

从系统的输入输出数据辨识Volterra核，辨识结果的准确度依赖于激励信号的选择。多音激励下的Volterra核辨识是一种简单易行的方法，然而关于多音激励如何选择问题，目前还没有得到有效解决。本文在多音激励信号频率成分选择的基础上，提出一种基于遗传算法的相位优化方法，在保证多音激励信号功率谱不失真的情况下可以有效的降低的波峰因子。实验验证了所提方法的有效性。该方法可广泛应用于系统辨识及动态特性测试，具有重要的应用价值。

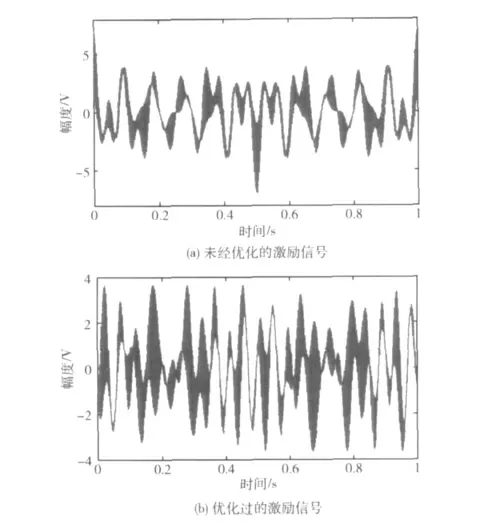
图7 关于Volterra核辨识的多音激励信号设计

［1］HAN Haitao，MA Hongguang，Li Fei，et al.Research on nonlinear system based on output frequency response function［J］.Journal of Engineering Design，2011，18（5）：373－377（in Chinese）.［韩海涛，马红光，李飞，等.基于系统输出频率响应函数的非线性系统研究［J］.工程设计学报，2011，18（5）：373－377.］

［2］MA Hongguang，HAN Chongzhao，KONG Xiangyu，et al.The GFRF identification model of radar fuze receiver［J］.Journal of System Simulation，2004，16（6）：1143－1146（in Chinese）.［马红光，韩崇昭，孔祥玉，等.基于电路仿真的接收机中频放大器的GFRF模型［J］.系统仿真学报，2004，16（6）：1143－1146.］

［3］HAN Haitao，MA Hongguang，HAN Kun，et al.Multitone stimulus signal design for identifying Volterra frequency domain kernels［J］.Journal of Engineering Design，2012，19（2）：123－127（in Chinese）.［韩海涛，马红光，韩琨，等.关于Volterra频域核辨识的多音激励信号设计［J］.工程设计学报，2012，19（2）：123－127.］

［4］LUO Hui，WANG Youren，LIN Hua，et al.Test stimulus optimization design of analog circuit based on random periodic stimulus function［J］.Acta Electronica Sinica，2011，39（8）：1950－1954（in Chinese）.［罗慧，王友仁，林华，等.任意周期激励函数的模拟电路测试激励优化设计［J］.电子学报，2011，39（8）：1950－1954.］

［5］JIANG Yuanyuan，WANG Youren，CUI Jiang，et al.Analog circuit test stimuli optimal method based on fault detectable analysis and genetic algorithm［J］.Application Research of Computers，2011，28（3）：930－934（in Chinese）.［姜媛媛，王友仁，崔江，等.基于故障可诊性与遗传算法的模拟电路测试激励优化方法［J］.计算机应用研究，2011，28（3）：930－934.］

［6］LUO Hui，WANG Youren，CUI Jiang，et al.Evolutionary generation of multi－tone sine stimulus for analog circuits based on fault distinguishable analysis［J］.Journal of Astronautics，2011，32（9）：2051－2058（in Chinese）.［罗慧，王友仁，崔江，等.基于故障可诊断性的模拟多音正弦测试信号进化生成［J］.宇航学报，2011，32（9）：2051－2058.］

［7］Steve Temme，Pascal Brunet.A new method for measu－ring distortion using a multitone stimulus and noncoherence［J］.Journal of Audio Engineering Society，2008，56（3）：176－188.

［8］Patrick Guillaume，Johan Schoukens，Rik Pintelon，et al.Crestfactor minimization using nonlinear Chebyshev approximation methods［J］.IEEE Transactions on Instrumentation and Measurement，1991，40（6）：982－989.

［9］Schroeder M.Synthesis of low－peak－factor signals and binary sequences with low autocorrelation［J］.IEEE Transactions on Information Theory，1970，16（1）：85－89.

［10］Edwin Van Der Ouderaa，Johan Schoukens，Jean Renneboog.Peak factor minimization using a time－frequency domain swapping algorithm［J］.IEEE Transactions on Instrumentation and Measurement，1988，37（1）：145－147.

［11］YAN Biao，WANG Haiyang，ZHU Yihuan.Multiphase complementary codes and their effect on reducing crestfactor of multitone signals［J］.Journal of Electronic Measurement and Instrument，2007，21（2）：49－53（in Chinese）.［颜彪，王海洋，朱一欢.多相互补码及其对多音频信号峰值因子的减少作用［J］.电子测量与仪器学报，2007，21（2）：49－53.］

［12］MENG Xiaofeng，ZHANG Fengjun，FU Luping.A study on numerical synthesis of low－peak－factor multisine signals［J］.Chinese Journal of Scientific Instrument，2002，23（5）：515－517（in Chinese）.［孟晓风，张凤均，付鲁平.低波峰因数多频正弦信号数字合成算法的研究［J］.仪器仪表学报，2002，23（5）：515－517.］

［13］Aadrew Horner，James Beauchamp.A genetic algorithm－based method for synthesis of low peak amplitude signals［J］.Journal of Audio Engineering Society，1996，99（1）：433－443.

［14］LEI Yingjie，ZHANG Shanwen，LI Xuwu.Genetic algorithm toolbox and its application MATLAB［M］.Xi’an：Xi’an Electronic and Science University Press，2006：1－30（in Chinese）.［雷英杰，张善文，李续武.MATLAB 遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2006：1－30.］